| Варианты появления xi | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2,0 | 2,5 | 3,0 | 3,5 | 4,0 | 4,5 | 5,0 | 5,5 | 6,0 | 6,5 | 7,0 | 7,5 | 8,0 | 8,5 |
| 1 | 2 | 10 | 37 | 72 | 90 | 101 | 80 | 60 | 40 | 28 | 10 | 4 | 2 |
Непрерывная случайная величина X имеет нормальный закон распределения с параметрами a и σ2, если ее плотность вероятности имеет вид:
где M(X) = a - математическое ожидание случайной величины X, σ2 - дисперсия случайной величины X.
Математическое ожидание дискретной случайной величины называется сумма произведений всех ее значений на соответствующие им вероятности:
Общее количество вариантов - 537.
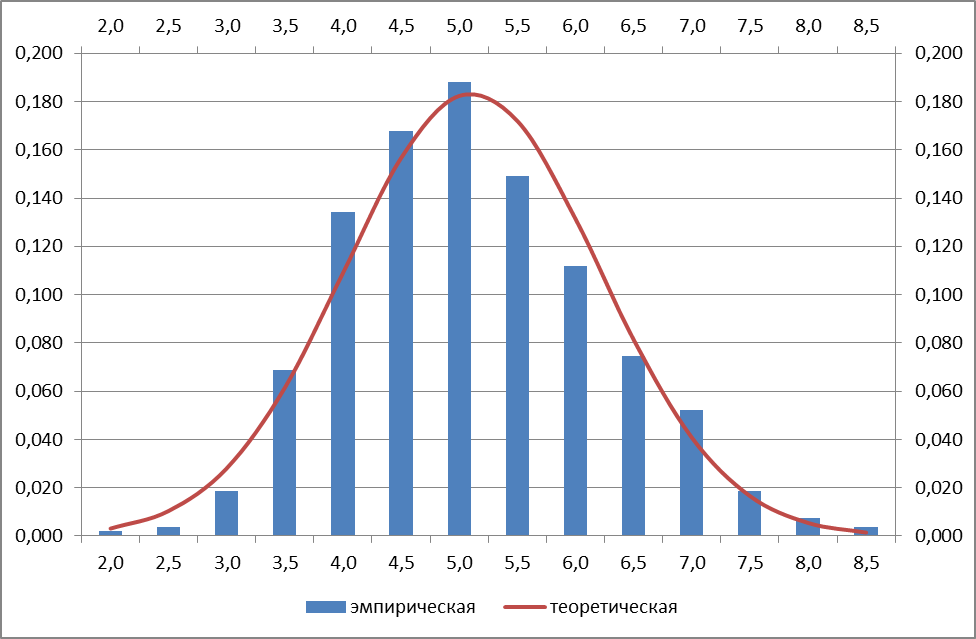
| xi | 2,0 | 2,5 | 3,0 | 3,5 | 4,0 | 4,5 | 5,0 | 5,5 | 6,0 | 6,5 | 7,0 | 7,5 | 8,0 | 8,5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| m(xi) | 1 | 2 | 10 | 37 | 72 | 90 | 101 | 80 | 60 | 40 | 28 | 10 | 4 | 2 |
| pi | 0,002 | 0,004 | 0,019 | 0,069 | 0,134 | 0,168 | 0,188 | 0,149 | 0,112 | 0,074 | 0,052 | 0,019 | 0,007 | 0,004 |
| φ(x) | 0,003 | 0,010 | 0,028 | 0,061 | 0,109 | 0,157 | 0,182 | 0,172 | 0,131 | 0,081 | 0,041 | 0,017 | 0,005 | 0,001 |
M(X) = 5,111.
Дисперсией случайной величины X называется математическое ожидание квадрата ее отклонения от математического ожидания:
Стандартное отклонение σx - арифметическое значение корня квадратного из дисперсии.
σx = 1,090.
Кривые теоретического и эмпирического распределения:

Для определения близости эмпирического распределения к нормальному теоретическому по методу Пирсона объединим наблюдения при x равном 2,0; 2,5 и 3,0, а также при x равном 8,0 и 8,5, так как для в каждом интервале должно быть не менее 5 наблюдений.