автоэвакуатор Красноярск дешево Владельцев автотранспорта, которому нужна эвакуация, часто беспокоит стоимость такой услуги. Автовакуатор Красноярск дешево - на сегодня это возможно. Дешевый эвакуатор очень востребован, и вызвать его легко.

Задание 2

По статистическим данным, приведенным в таблице 1, показывающим зависимость уровня технической обеспеченности семьи (проценты) от уровня ее дохода (тыс.руб.), провести эконометрический анализ в следующей последовательности.

Для определения вида зависимости построить корреляционное поле.
По расположению точек на корреляционном поле выдвинуть гипотезу о характере зависимости между исследуемыми признаками и выбрать уравнение регрессии.
Провести линеаризацию уравнения регрессии (привести к линейной форме).
Определить методом наименьших квадратов (МНК) коэффициенты линеаризованного уравнения регрессии. Для наглядности вычислений построить таблицу. Начертить график линеаризованного уравнения.
Определить параметры исходного уравнения регрессии и начертить график этого уравнения на корреляционном поле.
Для анализа силы зависимости между результативным и факторным признаками вычислить индекс корреляции. Проверить его значимость с вероятностью 0,95 по F-критерию Фишера. Сравнить значение индекса корреляции с линейным коэффициентом корреляции, полученным для линеаризованного уравнения регрессии.
Для оценки полученного уравнения регрессии проверить значимость с вероятностью 0,95 каждого коэффициента уравнения регрессии по t-критерию Стьюдента, скорректировать модель, если это необходимо.
Рассчитать коэффициент детерминации, сделать вывод об общем качестве полученного уравнения регрессии.
Определить точность уравнения регрессии по средней ошибке аппроксимации.
С вероятностью 0,95 построить точечный и интервальный прогноз ожидаемого значения результативного признака, в предположении, что значение признака-фактора увеличится на 10% относительно своего среднего уровня.

Таблица 1. **Исходные данные**
i	1	2	3	4	5	6	7	8	9	10	11	12
X_i	5	10	15	25	40	60	85	100	120	145	160	180
Y_i	0,7	0,9	1,2	2,3	5,1	11,8	40,4	56,9	81,6	94,8	97,7	99,2

Решение

Корреляционное поле

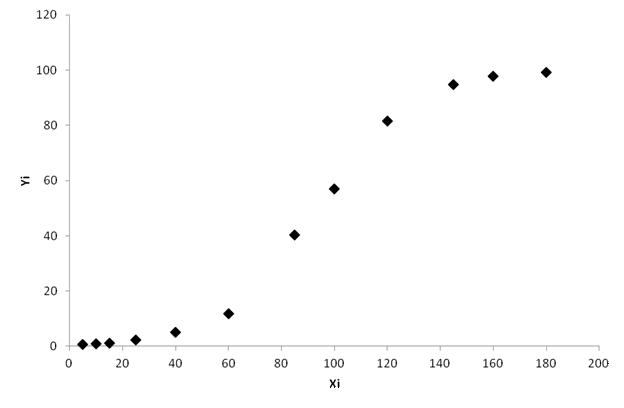
Рис.1. Корреляционное поле

Гипотеза о характере зависимости между исследуемыми признаками и выбор уравнения регрессии

Анализ рис.1 позволяет сделать вывод о наличии между факторным и результативным признаками зависимости типа логистической кривой Перла-Рида, выражающейся функцией:

y=\frac{L}{1+ae^{-bx}},

где y - результативный признак;
x - факторный признак;
L - верхний предел переменной y;
a и b - параметры.

В данном случае L=100.

Будем искать уравнение регрессии в виде:

y=\frac{100}{1+ae^{-bx}}.

Линеаризация уравнения регрессии

Проведем линеаризацию уравнения:

y=\frac{100}{1+ae^{-bx}},

\frac{100}{y}=1+ae^{-bx},

\frac{100}{y}-1=ae^{-bx},

\ln\left(\frac{100}{y}-1\right)=\ln\left(ae^{-bx}\right),

\ln\left(\frac{100}{y}-1\right)=\ln{a}-bx.

Введем новые переменные и параметры:

y^\prime=\ln\left(\frac{100}{y}-1\right),

x^\prime=x,

a^\prime=\ln{a},

b^\prime=-b.

После преобразования получаем модель линейной регрессии:

y^\prime=a^\prime+b^\prime x^\prime.

Определение коэффициентов линеаризованного уравнения

Коэффициенты уравнения определим по формулам:

b^\prime=\frac{\overline{y^\prime\cdot x^\prime}-\overline{y^\prime}\cdot\overline{x^\prime}}{\overline{{x^\prime}^2}-{\overline{x^\prime}}^2},

a^\prime=\overline{y^\prime}-b^\prime\cdot\overline{x^\prime}

где

\overline{x^\prime}=\frac{1}{n}\sum_{i=1}^{n}x_i^\prime;

\overline{{x^\prime}^2}=\frac{1}{n}\sum_{i=1}^{n}x_i^{\prime^2};

\overline{y^\prime\cdot x^\prime}=\frac{1}{n}\sum_{i=1}^{n}{y_i^\prime x_i^\prime};

\overline{y^\prime}=\frac{1}{n}\sum_{i=1}^{n}y_i^\prime.

Таблица 2. **Вспомогательные вычисления**
i	x	y	x^\prime	y^\prime	y^\prime\cdot x^\prime	{x^\prime}^2
1	5	0,7	5	4,955	24,774	25
2	10	0,9	10	4,701	47,015	100
3	15	1,2	15	4,411	66,162	225
4	25	2,3	25	3,749	93,725	625
5	40	5,1	40	2,924	116,943	1600
6	60	11,8	60	2,012	120,690	3600
7	85	40,4	85	0,389	33,050	7225
8	100	56,9	100	-0,278	-27,777	10000
9	120	81,6	120	-1,489	-178,737	14400
10	145	94,8	145	-2,903	-420,951	21025
11	160	97,7	160	-3,749	-599,839	25600
12	180	99,2	180	-4,820	-867,651	32400
Итого	945	492,6	945	9,900	-1592,596	116825
Среднее	78,75	41,05	78,75	0,825	-132,716	9735,42

b^\prime=\frac{\overline{y^\prime\cdot x^\prime}-\overline{y^\prime}\cdot\overline{x^\prime}}{\overline{{x^\prime}^2}-{\overline{x^\prime}}^2}=\frac{-132,716-0,825\cdot 78,75}{9735,42-78,75^2}=-0,056,

a^\prime=\overline{y^\prime}-b^\prime\cdot\overline{x^\prime}=0,825-0,056\cdot 78,75=5,230.

Линеаризованное уравнение:

y=-0,056\cdot x+5,230.

График линеаризованного уравнения:

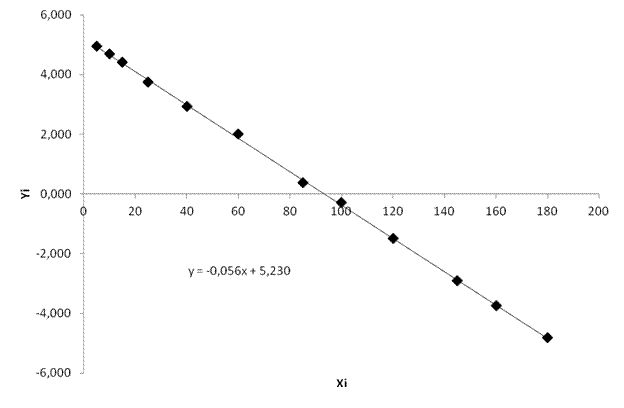
Рис.2. График линеаризованного уравнения

Параметры исходного уравнения и график его на корреляционном поле

Параметры исходной нелинейной модели:

a=e^{5,230}=186,865;

b=-b^\prime=0,056.

Модель:

\tilde y=\frac{100}{1+186,865\cdot e^{-0,056x}}.

Таблица 3. **Вспомогательные вычисления**
i	x	y	\tilde y
1	5	0,7	0,703
2	10	0,9	0,928
3	15	1,2	1,223
4	25	2,3	2,121
5	40	5,1	4,775
6	60	11,8	13,309
7	85	40,4	38,334
8	100	56,9	58,994
9	120	81,6	81,496
10	145	94,8	94,690
11	160	97,7	97,634
12	180	99,2	99,215
Итого	945	492,6	493,422
Среднее	78,75	41,05	41,118

Совместный график модели и поля корреляции:

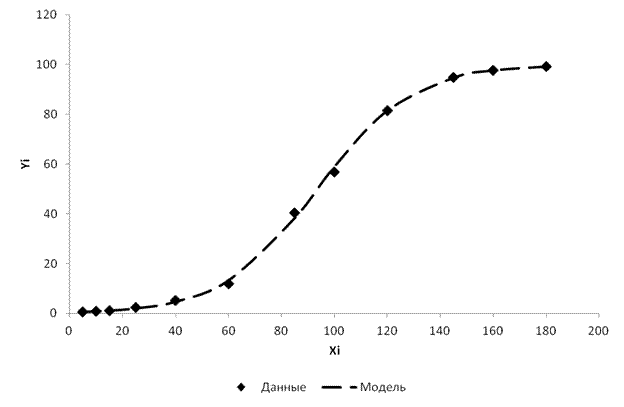
Рис.3. Совместный график исходных данных и данных по модели

Индекс корреляции и его значимость

Для измерения тесноты связи при криволинейной форме зависимости используется корреляционное отношение, формула которого имеет следующий вид:

\rho=\sqrt{1-\frac{\sum\left(y_i-\tilde{y}_i\right)^2}{\sum\left(y_i-\bar{y}_i\right)^2}}

Таблица 4. **Вспомогательные вычисления**
i	x_i	y_i	\tilde{y}_i	y_i-\tilde{y}_i	\left(y_i-\tilde{y}_i\right)^2	y_i-\bar{y}_i	\left(y_i-\bar{y}_i\right)^2
1	5	0,7	0,703	-0,003	0,000	-40,350	1628,123
2	10	0,9	0,928	-0,028	0,001	-40,150	1612,023
3	15	1,2	1,223	-0,023	0,001	-39,850	1588,023
4	25	2,3	2,121	0,179	0,032	-38,750	1501,563
5	40	5,1	4,775	0,325	0,105	-35,950	1292,403
6	60	11,8	13,309	-1,509	2,277	-29,250	855,563
7	85	40,4	38,334	2,066	4,269	-0,650	0,422
8	100	56,9	58,994	-2,094	4,385	15,850	251,223
9	120	81,6	81,496	0,104	0,011	40,550	1644,303
10	145	94,8	94,690	0,110	0,012	53,750	2889,063
11	160	97,7	97,634	0,066	0,004	56,650	3209,223
12	180	99,2	99,215	-0,015	0,000	58,150	3381,423
Итого	945	492,6			11,096		19853,350
Среднее	78,75	41,05

\rho=\sqrt{1-\frac{11,096}{19853,350}}=0,99972.

F-критерий Фишера определим по формуле:

F=\frac{\rho^2}{1-\rho^2}\cdot\frac{n-m-1}{m}.

n - число наблюдений;
m - число факторных параметров.

F=\frac{{0,99972}^2}{1-{0,99972}^2}\cdot\frac{12-1-1}{1}=21456,467.

F>F_{табл}=4,965\quad для\quad\alpha=0,05;\quad k_1=m=1,\quad k_2=n-m-1=10.

Уравнение регрессии с вероятностью 0,95 в целом статистически значимо.

Индекс корреляции линейной модели найдем по формуле:

r_{y,x}=\frac{\sum{\left(y^\prime-\bar{y}^\prime\right)\cdot \left(x^\prime-\bar{x}^\prime\right)}}{\sqrt{\sum{\left(y^\prime-\bar{y}^\prime \right)}^2\cdot\sum{\left(x^\prime-\bar{x}^\prime\right)}^2}}.

Таблица 5. **Вспомогательные вычисления**
i	x^\prime	y^\prime	x^\prime-\bar{x}^\prime	y^\prime-\bar{y}^\prime	\left(y^\prime-\bar{y}^\prime\right)\cdot\left(x^\prime-\bar{x}^\prime\right)	\left(x^\prime-\bar{x}^\prime\right)^2	\left(y^\prime-\bar{y}^\prime\right)^2
1	5	4,955	-73,75	4,130	-304,572	5439,063	17,055
2	10	4,701	-68,75	3,876	-266,507	4726,563	15,027
3	15	4,411	-63,75	3,586	-228,591	4064,063	12,858
4	25	3,749	-53,75	2,924	-157,163	2889,063	8,550
5	40	2,924	-38,75	2,099	-81,319	1501,563	4,404
6	60	2,012	-18,75	1,186	-22,246	351,563	1,408
7	85	0,389	6,25	-0,436	-2,726	39,063	0,190
8	100	-0,278	21,25	-1,103	-23,435	451,563	1,216
9	120	-1,489	41,25	-2,315	-95,473	1701,563	5,357
10	145	-2,903	66,25	-3,728	-246,989	4389,063	13,899
11	160	-3,749	81,25	-4,574	-371,639	6601,563	20,922
12	180	-4,820	101,25	-5,645	-571,588	10251,563	31,870
Итого	945	9,900			-2372,249	42406,250	132,755
Среднее	78,75	0,825

r_{y,x}=\frac{-2372,249}{\sqrt{42406,250\cdot 132,775}}=-0,99982.

Вывод: значения коэффициента корреляции для линеаризованного уравнения и нелинейного уравнения практически совпадают по модулю, но имеют противоположные знаки, поскольку y^\prime и x^\prime связаны обратно пропорциональной зависимостью.

Проверка значимости каждого уравнения регрессии по t-критерию Стьюдента

Величины случайной ошибки коэффициентов регрессии и корреляции найдем по формулам:

t_b=\frac{b}{\sqrt{\frac{\sum{\left(y-\hat y\right)^2}}{(n-2)\cdot\sum{\left(x-\bar x\right)^2}}}},

t_a=\frac{a}{\sqrt{\frac{\sum\left(y-\hat y\right)^2}{n-2}\cdot\frac{\sum{x^2}}{n\cdot\sum{\left(x-\bar x\right)^2}}}},

t_r=\frac{r_{xy}}{\sqrt{\frac{1-r^2_{xy}}{n-2}}}.

Таблица 6. Вспомогательные вычисления

Таблица 6. **Вспомогательные вычисления**
i	x	y	\hat y	y-\hat y	\left(y-\hat y\right)^2	x-\bar x	\left(x-\bar x\right)^2	x^2
1	5	0,7	0,70	0,00	0,000	-73,75	5439,063	25
2	10	0,9	0,93	-0,03	0,001	-68,75	4726,563	100
3	15	1,2	1,22	-0,02	0,001	-63,75	4064,063	225
4	25	2,3	2,12	0,18	0,032	-53,75	2889,063	625
5	40	5,1	4,78	0,32	0,105	-38,75	1501,563	1600
6	60	11,8	13,31	-1,51	2,277	-18,75	351,563	3600
7	85	40,4	38,33	2,07	4,269	6,25	39,063	7225
8	100	56,9	58,99	-2,09	4,385	21,25	451,563	10000
9	120	81,6	81,50	0,10	0,011	41,25	1701,563	14400
10	145	94,8	94,69	0,11	0,012	66,25	4389,063	21025
11	160	97,7	97,63	0,07	0,004	81,25	6601,563	25600
12	180	99,2	99,21	-0,01	0,000	101,25	10251,563	32400
Итого					11,096		42406,250	116825
Среднее	78,75

t_b=\frac{b}{\sqrt{\frac{\sum{\left(y-\hat y\right)^2}}{(n-2)\cdot\sum{\left(x-\bar x\right)^2}}}}=\frac{-0,056}{\sqrt{\frac{11,096}{(12-2)\cdot 42406,250}}}=-10,236,

t_a=\frac{a}{\sqrt{\frac{\sum\left(y-\hat y\right)^2}{n-2}\cdot\frac{\sum{x^2}}{n\cdot\sum{\left(x-\bar x\right)^2}}}}=\frac{186,865}{\sqrt{\frac{11,096}{12-2}\cdot\frac{116825}{12\cdot 42406,250}}}=10,363,

t_r=\frac{r_{xy}}{\sqrt{\frac{1-r^2_{xy}}{n-2}}}=\frac{0,99972}{\sqrt{\frac{1-{0,99972}^2}{12-2}}}=133,724.

Табличное значение t-критерия Стьюдента при \alpha=0,05, k=n-m-1=10 t_{табл}=2,228. Модули расчетных значений t-критерия превосходят табличное. Следовательно, коэффициенты уравнения и регрессии считаются значимыми.

Расчет коэффициента детерминации

Коэффициент детерминации определяется по формуле:

R^2=r^2_{xy}={0,99972}^2=0,99944.

Вывод: вариация результата y на 99,99\% объясняется вариацией фактора x.

Определение средней ошибки аппроксимации:

Среднюю ошибку определим по формуле:

\bar A=\frac{1}{n}\cdot\sum{\frac{\left|y-\hat y\right|}{y}}\cdot 100\%.

Таблица 7. **Вспомогательные вычисления**
i	x	y	\hat y	y-\hat y	\left\|y-\hat y\right\|	\frac{\left\|y-\hat y\right\|}{y}
1	5	0,7	0,703	-0,003	0,003	0,004
2	10	0,9	0,928	-0,028	0,028	0,031
3	15	1,2	1,223	-0,023	0,023	0,019
4	25	2,3	2,121	0,179	0,179	0,078
5	40	5,1	4,775	0,325	0,325	0,064
6	60	11,8	13,309	-1,509	1,509	0,128
7	85	40,4	38,334	2,066	2,066	0,051
8	100	56,9	58,994	-2,094	2,094	0,037
9	120	81,6	81,496	0,104	0,104	0,001
10	145	94,8	94,690	0,110	0,110	0,001
11	160	97,7	97,634	0,066	0,066	0,001
12	180	99,2	99,215	-0,015	0,015	0,000
Итого						0,415

\bar A=\frac{1}{n}\cdot\sum{\frac{\left|y-\hat y\right|}{y}}\cdot 100\%=\frac{0,415}{12}\cdot 100\%=3,46\%.

В среднем расчетные значения отклоняются от фактических на 3,46\%.

Точечный и интервальный прогноз ожидаемого значения результативного признака

Среднее значение признака-фактора - 78,75. Ожидаемое значение признака-фактора:

x_п=78,75\cdot 1,1=86,625.

Точечное прогнозное значение:

y_п=\frac{100}{1+186,865\cdot e^{-0,056x}}=\frac{100}{1+186,865\cdot e^{-0,056\cdot 86,625}}=40,504.

Доверительный интервал найдем по формуле:

\Delta_{y_п}=t_{табл}\cdot\sqrt{\frac{\sum\left(y-\hat y\right)^2}{n-2}}\cdot\sqrt{1+\frac{1}{n}+\frac{\left(x_п-\bar x\right)^2}{\sum{\left(x-\bar x\right)^2}}}=

=2,228\cdot\sqrt{\frac{11,096}{10}}\cdot\sqrt{1+\frac{1}{12}+\frac{\left(86,625-78,75\right)^2}{42406,250}}=2,445.

y_п=40,504\pm 2,445.

38,060\le y_п\le 42,949.

косметическая чистка лица

Пользователь, раз уж ты добрался до этой строки, ты нашёл тут что-то интересное или полезное для себя. Надеюсь, ты просматривал сайт в браузере Firefox, который один правильно отражает формулы, встречающиеся на страницах. Если тебе понравился контент, помоги сайту материально. Отключи, пожалуйста, блокираторы рекламы и нажми на пару баннеров вверху страницы. Это тебе ничего не будет стоить, увидишь ты только то, что уже искал или ищешь, а сайту ты поможешь оставаться на плаву.