магазин виски в москве Если вам нужен редкий и эксклюзивный напиток, мы приложим максимум усилий, чтобы найти его вам и привезти. Узнать все про виски, поучаствовать в дегустациях или мастер-классах можно, написав нам по электронной почте. Желаем приятного и правильного выбора на страницах нашего магазина!
Задание 1
Для анализа инвестирования предприятий собственными средствами в регионе проведена 10%-ная механическая выборка, в результате которой получены следующие данные, млн.руб.:
| № предприятия | Нераспределенная прибыль | Инвестиции в основные фонды | № предприятия | Нераспределенная прибыль | Инвестиции в основные фонды |
|---|---|---|---|---|---|
| 1 | 2,7 | 0,37 | 14 | 3,9 | 0,58 |
| 2 | 4,8 | 0,90 | 15 | 4,2 | 0,57 |
| 3 | 6,0 | 0,96 | 16 | 5,6 | 0,78 |
| 4 | 4,7 | 0,68 | 17 | 4,5 | 0,65 |
| 5 | 4,4 | 0,60 | 18 | 3,8 | 0,59 |
| 6 | 4,3 | 0,61 | 19 | 2,0 | 0,16 |
| 7 | 5,0 | 0,65 | 20 | 4,8 | 0,72 |
| 8 | 3,4 | 0,51 | 21 | 5,2 | 0,63 |
| 9 | 2,3 | 0,35 | 22 | 2,2 | 0,24 |
| 10 | 4,5 | 0,70 | 23 | 3,6 | 0,45 |
| 11 | 4,7 | 0,80 | 24 | 4,1 | 0,57 |
| 12 | 5,4 | 0,74 | 25 | 3,3 | 0,45 |
| 13 | 5,8 | 0,92 |
- Постройте статистический ряд распределения предприятий по признаку - инвестиции в основные фонды, образовав четыре группы с равными интервалами.
- Постройте графики полученного ряда распределения: гистограмму и кумуляту. Графически определите значения моды и медианы.
- Рассчитайте характеристики интервального ряда распределения: среднюю арифметическую, среднее квадратическое отклонение, коэффициент вариации, моду и медиану.
- Вычислите среднюю арифметическую по исходным данным, сравните ее с аналогичным показателем, рассчитанным в п.3 для интервального ряда распределения. Объясните причину их расхождения. Сделайте выводы по результатам выполнения задания.
Решение
- Построим статистический ряд распределения предприятий по признаку
- инвестиции в основные фонды, образовав четыре группы с
равными интервалами.
Исходные данные:
Отсортируем исходные данные по параметру инвестиции в основные фонды:№ предприятия Нераспределенная прибыль Инвестиции в основные фонды 1 2,7 0,37 2 4,8 0,90 3 6,0 0,96 4 4,7 0,68 5 4,4 0,60 6 4,3 0,61 7 5,0 0,65 8 3,4 0,51 9 2,3 0,35 10 4,5 0,70 11 4,7 0,80 12 5,4 0,74 13 5,8 0,92 14 3,9 0,58 15 4,2 0,57 16 5,6 0,78 17 4,5 0,65 18 3,8 0,59 19 2,0 0,16 20 4,8 0,72 21 5,2 0,63 22 2,2 0,24 23 3,6 0,45 24 4,1 0,57 25 3,3 0,45
Для изучения структуры предприятий по инвестициям в основные фонды построим интервальный вариационный ряд. Величина интервала равна:№ предприятия Инвестиции в основные фонды 19 0,16 22 0,24 9 0,35 1 0,37 23 0,45 25 0,45 8 0,51 15 0,57 24 0,57 14 0,58 18 0,59 5 0,6 6 0,61 21 0,63 7 0,65 17 0,65 4 0,68 10 0,7 20 0,72 12 0,74 16 0,78 11 0,8 2 0,9 13 0,92 3 0,96 h=\frac{x_{max}-x_{min}}{n}=\frac{0,96-0,16}{4}=0,2.Разработочная таблица для построения интервального ряда и аналитической группировки:
Распределение предприятий по инвестициям в основные фонды:Группы предприятий по инвестициям в основные фонды № предприятия Инвестиции в основные фонды 0,16-0,36 19 0,16 22 0,24 9 0,35 Всего 3 0,75 0,36-0,56 1 0,37 23 0,45 25 0,45 8 0,51 Всего 4 1,78 0,56-0,76 15 0,57 24 0,57 14 0,58 18 0,59 5 0,6 6 0,61 21 0,63 7 0,65 17 0,65 4 0,68 10 0,7 20 0,72 12 0,74 Всего 13 8,29 0,76-0,96 16 0,78 11 0,8 2 0,9 13 0,92 3 0,96 Всего 5 4,36
Структура предприятий по инвестициям в основные фонды:№ группы Группы предприятий по инвестициям в основные фонды Число предприятий в абсолютном выражении в относительных единицах, % 1 0,16-0,36 3 12% 2 0,36-0,56 4 16% 3 0,56-0,76 13 52% 4 0,76-0,96 5 20% Итого 25 100%
Вывод. Анализ интервального ряда распределения изучаемой совокупности предприятий показывает, что распределение предприятий по инвестициям в основные фонды не является равномерным. Преобладают предприятия с инвестициями от 0,56 млн.руб. до 0,76 млн.руб. Это 13 предприятий, доля которых составляет 52%. 28% предприятий имеют инвестиции в основные фонды менее 0,56 млн.руб., 80% - менее 0,76 млн.руб. 12% - менее 0,36 млн.руб.№ группы Группы предприятий по инвестициям в основные фонды Число предприятий Накопленная частота Накопленная частость в абсолютном выражении в относительных единицах, % 1 0,16-0,36 3 12% 3 12% 2 0,36-0,56 4 16% 7 28% 3 0,56-0,76 13 52% 20 80% 4 0,76-0,96 5 20% 25 100% Итого 25 100% - Построим графики полученного ряда распределения: гистограмму и
кумуляту. Графически определите значения моды и медианы.
Определение моды графическим методом:
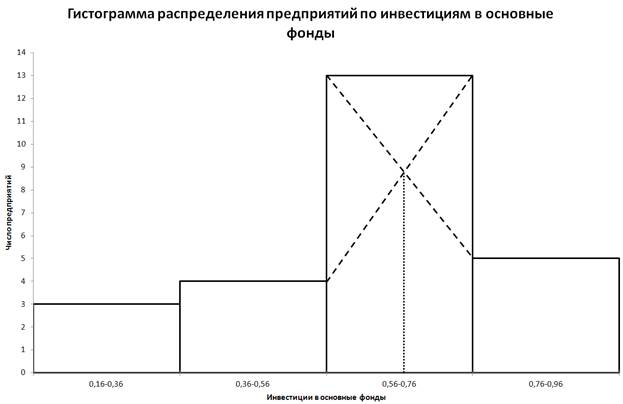
Приблизительное значение моды, вычисленное графическим методом - 0,665 - центральное значение интервала, имеющего наибольшую частоту.
Определение медианы графическим методом:
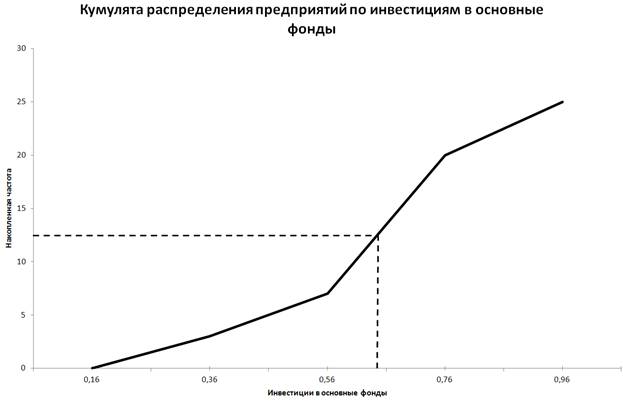
Приблизительное значение медианы, вычисленное графическим методом - 0,63 - значение признака, приходящееся на середину ранжированного ряда.
Вывод. Для рассматриваемой совокупности предприятий наиболее распространенный объем инвестиций в основные фонды характеризуется средней величиной 0,665 млн.руб. В рассматриваемой совокупности предприятий половина предприятий имеет в среднем объем инвестиций в основные средства не более 0,63 млн.руб., а другая половина - не менее 0,63 млн.руб. - Рассчитаем характеристики интервального ряда распределения:
среднюю арифметическую, среднее квадратическое отклонение,
коэффициент вариации, моду и медиану.
Расчетная таблица для нахождения характеристик ряда распределения:
Расчет средней арифметической взвешенной:Группы предприятий по инвестициям в основные фонды Середина интервала, x_j^' Число предприятий, f_j x_j^'\cdot f_j x_j^'-\overline{x} (x_j^'-\overline{x})^2 (x_j^'-\overline{x})^2\cdot f_j 0,16-0,36 0,26 3 0,78 -0,36 0,13 0,39 0,36-0,56 0,46 4 1,84 -0,16 0,03 0,10 0,56-0,76 0,66 13 8,58 0,04 0,00 0,02 0,76-0,96 0,86 5 4,3 0,24 0,06 0,29 Итого 25 16 0,80 \overline{x}=\frac{\sum\limits_{j=1}^k x_j^'\cdot f_j}{\sum\limits_{j=1}^k f_j}=\frac{16}{25}=0,62\ млн.руб.Расчет среднего квадратического отклонения:\sigma=\sqrt{\frac{\sum\limits_{j=1}^k (x_j^'-\overline{x})^2\cdot f_j}{\sum\limits_{j=1}^k f_j}}=\sqrt{\frac{0,80}{25}}=0,18\ млн.руб.Расчет коэффициента вариации:V_{\sigma}=\frac{\sigma}{\overline{x}}\times 100=\frac{0,18}{0,62}\times 100=28,85\%.Расчет моды:Mo=x_{Mo}+h\cdot\frac{f_{Mo}-f_{Mo-1}}{(f_{Mo}-f_{Mo-1})- (f_{Mo}-f_{Mo+1})},где x_{Mo}- нижняя граница модального интервала; h - величина модального интервала; f_{Mo} - частота модального интервала; x_{Mo-1} - частота интервала, предшествующего модальному; x_{Mo+1} - частота интервала, следующего за модальным.Mo=0,56+0,2\cdot\frac{13-4}{(13-4)-(13-5)}=0,67\ млн.руб.Расчет медианы:Me=x_{Me}+h\cdot\frac{\frac{\sum\limits_{j=1}^k f_j}{2}-S_{Me-1}}{f_{Me}},где x_{Me} - нижняя граница медианного интервала; h - величина медианного интервала; \sum\limits_{j=1}^k f_j - сумма всех частот; f_{Me} - частота медианного интервала; S_{Me-1} - кумулятивная (накопленная) частота интервала, предшествующего медианному.Me=0,56+0,2\cdot\frac{\frac{25}{2}-7}{13}=0,64\ млн.руб.Вывод. Анализ полученных значений показывает, что средний объем инвестиций в основные фонды для предприятий составляет 0,62 млн.руб. Отклонение от среднего объема составляет в среднем 0,18 млн.руб. Наиболее характерные значе6ния инвестиций в основные фонды находятся в пределах от 0,44 до 0,80 млн.руб. Значение коэффициента вариации (28,85%) не превышает 33%, следовательно, вариация инвестиций в основные фонды в исследуемой совокупности незначительна и совокупность по данному признаку качественно однородна. Расхождения между значениями средней, моды и медианы (0,62 млн.руб., 0,67 млн.руб., 0,64 млн.руб.) незначительно, что подтверждает вывод об однородности совокупности предприятий. Таким образом найденное среднее значение инвестиций в основные фонды является типичной, надежной характеристикой исследуемой совокупности предприятий. - Вычислим среднюю арифметическую по исходным данным, сравним ее с
аналогичным показателем, рассчитанным в п.3 для интервального ряда
распределения. Объясним причину их расхождения.
Средняя арифметическая простая:\overline{x}=\frac{\sum\limits_{i=1}^n x_i}{n}=\frac{15,18}{25}=0,61\ млн.руб.Причина расхождения средних величин заключается в том, что простая средняя определяется по фактическим значениям для всех предприятий, а средняя взвешенная вычисляется для интервального ряда, когда в качестве значений признака берутся середины интервалов. Значение средней взвешенной менее точное, если нет равномерного распределения значений признака внутри каждой группы.
Задание 2
По исходным данным:
- Установите наличие и характер связи между признаками нераспределенная прибыль и инвестиции в основные фонды методом аналитической группировки, образовав четыре группы с равными интервалами по факторному признаку.
- Измерьте тесноту корреляционной связи между названными признаками с использованием коэффициента детерминации и эмпирического корреляционного отношения. Сделайте выводы по результатам выполнения задания.
Решение
- Установим наличие и характер связи между признаками нераспределенная
прибыль и инвестиции в основные фонды методом
аналитической группировки, образовав четыре группы с равными
интервалами по факторному признаку.
Разработочная таблица:
Зависимость нераспределенной прибыли от инвестиций в основные фонды:Группы предприятий по инвестициям в основные фонды № предприятия Инвестиции в основные фонды Нераспределенная прибыль 0,16-0,36 19 0,16 2 22 0,24 2,2 9 0,35 2,3 Всего 3 0,75 6,5 0,36-0,56 1 0,37 2,7 23 0,45 3,6 25 0,45 3,3 8 0,51 3,4 Всего 4 1,78 13 0,56-0,76 15 0,57 4,2 24 0,57 4,1 14 0,58 3,9 18 0,59 3,8 5 0,6 4,4 6 0,61 4,3 21 0,63 5,2 7 0,65 5 17 0,65 4,5 4 0,68 4,7 10 0,7 4,5 20 0,72 4,8 12 0,74 5,4 Всего 13 8,29 58,8 0,76-0,96 16 0,78 5,6 11 0,8 4,7 2 0,9 4,8 13 0,92 5,8 3 0,96 6 Всего 5 4,36 26,9
Вывод. Анализ данных таблицы показывает, что с увеличением инвестиций в основные фонды от группы к группе систематически возрастает и нераспределенная прибыль по каждой группе предприятий, что свидетельствует о наличии прямой корреляционной связи между исследуемыми признаками.№ группы Группы предприятий по инвестициям в основные фонды Число предприятий Нераспределенная прибыль Всего В среднем на одно предприятие 1 0,16-0,36 3 6,5 2,17 2 0,36-0,56 4 13 3,25 3 0,56-0,76 13 58,8 4,52 4 0,76-0,96 5 26,9 5,38 Итого 25 105,2 3,83 - Измерим тесноту корреляционной связи между названными признаками
с использованием коэффициента детерминации и эмпирического
корреляционного отношения.
Эмпирический коэффициент детерминации \eta^2рассчитывается как доля межгрупповой дисперсии в общей дисперсии по формуле:\eta^2=\frac{\delta_x^2}{\sigma_о^2},где \sigma_о^2 - общая дисперсия признака нераспределенная прибыль, \delta_x^2 - межгрупповая (факторная) дисперсия признака нераспределенная прибыль.
Общая дисперсия вычисляется по формуле:\sigma_о^2=\frac{\sum\limits_{i=1}^n (y_i-\overline{y}_0)^2}{n},где y_i - индивидуальные значения нераспределенной прибыли; \overline{y}_0 - общая средняя значений нераспределенной прибыли; n - число единиц совокупности.
Общая средняя \overline{y}_0 вычисляется по формуле:
\overline{y}_0=\frac{\sum\limits_{i=1}^n y_i}{n}.Вспомогательная таблица для расчета общей дисперсии:№ предприятия Нераспределенная прибыль y_i-\overline{y}_0 (y_i-\overline{y}_0)^2 1 2,7 -1,51 2,274 2 4,8 0,59 0,350 3 6,0 1,79 3,211 4 4,7 0,49 0,242 5 4,4 0,19 0,037 6 4,3 0,09 0,008 7 5,0 0,79 0,627 8 3,4 -0,81 0,653 9 2,3 -1,91 3,640 10 4,5 0,29 0,085 11 4,7 0,49 0,242 12 5,4 1,19 1,421 13 5,8 1,59 2,534 14 3,9 -0,31 0,095 15 4,2 -0,01 0,000 16 5,6 1,39 1,938 17 4,5 0,29 0,085 18 3,8 -0,41 0,166 19 2,0 -2,21 4,875 20 4,8 0,59 0,350 21 5,2 0,99 0,984 22 2,2 -2,01 4,032 23 3,6 -0,61 0,370 24 4,1 -0,11 0,012 25 3,3 -0,91 0,824 Итого 105,2 0,00 29,058 \overline{y}_0=\frac{105,2}{25}=4,21.\sigma^2=\frac{29,058}{25}=1,16.Показатель \delta_x^2 вычисляется по формуле:\delta_x^2=\frac{\sum\limits_{j=1}^k (\overline{y}_j-\overline{y}_0)^2\cdot f_j}{\sum\limits_{j=1}^k f_j},где \overline{y}_j - групповые средние; \overline{y}_0 - общая средняя; f_j - число единиц в j-й группе; k - число групп.
Вспомогательная таблица для расчета межгрупповой дисперсии:Группы предприятий по инвестициям в основные фонды Число предприятий, f_j Среднее значение \overline{y}_j в группе \overline{y}_j-\overline{y}_0 (\overline{y}_j-\overline{y}_0)^2\cdot f_j 0,16-0,36 3 2,17 -2,04 12,501 0,36-0,56 4 3,25 -0,96 3,671 0,56-0,76 13 4,52 0,32 1,291 0,76-0,96 5 5,38 1,17 6,868 Итого 25 24,331 \delta_x^2=\frac{24,331}{25}=0,97.\eta^2=\frac{0,97}{1,16}=0,837\ или\ 83,7\%.Вывод. 83,7% вариации нераспределенной прибыли обусловлено вариацией инвестиций в основные фонды, а 16,3% - влиянием прочих неучтенных факторов.
Эмпирическое корреляционное отношение \eta вычисляется по формуле:\eta=\sqrt{\eta^2}=\sqrt{0,837}=0,915.Вывод. Согласно шкале Чэддока связь между инвестициями в основные фонды и нераспределенной прибылью предприятий является весьма тесной.
Задание 3
По результатам выполнения задания 1 с вероятностью 0,954 определите:
- Среднюю и предельную ошибку выборки среднего размера инвестиций и границы, в которых будет находиться средний размер инвестиций в генеральной совокупности.
- Среднюю и предельную ошибку выборки доли предприятий с инвестициями в основные фонды 0,76 млн.руб. и более и границы, в которых будет находиться генеральная доля.
Решение
- Найдем среднюю и предельную ошибку выборки среднего размера
инвестиций и границы, в которых будет находиться средний размер
инвестиций в генеральной совокупности.
Средняя ошибка выборки \mu_{\widetilde{x}} определяется по формуле:\mu_{\widetilde{x}}=\sqrt{\frac{\sigma^2}{n}\cdot \left(1-\frac{n}{N}\right)},где \sigma^2 - общая дисперсия выборочных значений признаков; N - число единиц в генеральной совокупности, n - число единиц в выборочной совокупности.N=\frac{n}{10\%}=\frac{25}{10\%}=250.\mu_{\widetilde{x}}=\sqrt{\frac{0,18^2}{25}\cdot \left(1-\frac{25}{250}\right)}=0,034.Предельная ошибка выборки \Delta_{\widetilde{x}} выражается формулой:\Delta_{\widetilde{x}}=t(P)\cdot \mu_{\widetilde{x}}.P=0,954, в этом случае t=2,0.\Delta_{\widetilde{x}}=2,0\cdot 0,034=0,068.Доверительный интервал вычисляется из выражения:\overline{x}=\widetilde{x}\pm\Delta_{\widetilde{x}},\widetilde{x}-\Delta_{\widetilde{x}}\le\overline{x}\le \widetilde{x}+\Delta_{\widetilde{x}},где \widetilde{x} - выборочная средняя, \overline{x} - генеральная средняя.0,62-0,068\le\overline{x}\le 0,62+0,068,0,552\le\overline{x}\le 0,688.Вывод. На основании проведенного выборочного обследования предприятий с вероятностью 0,954 можно утверждать, что для генеральной совокупности предприятий средний размер инвестиций находится в пределах от 0,552 млн.руб. до 0,688 млн.руб. - Найдем среднюю и предельную ошибку выборки доли предприятий с
инвестициями в основные фонды 0,76 млн.руб. и более и границы, в
которых будет находиться генеральная доля.
Средняя выборка доли вычисляется по формуле:w=\frac{m}{n},где m - число единиц совокупности, обладающих заданным свойством, n - общее число единиц в совокупности.w=\frac{5}{25}=0,2.Предельная ошибка выборки рассчитывается по формуле:\Delta_w=t\cdot\sqrt{\frac{w\cdot(1-w)}{n}\cdot \left(1-\frac{n}{N}\right)},\Delta_w=2\cdot\sqrt{\frac{0,2\cdot(1-0,2)}{25}\cdot \left(1-\frac{25}{250}\right)}=0,15.Вывод. С вероятностью 0,954 можно утверждать, что в генеральной совокупности предприятий доля предприятий с размером инвестиций в основные фонды 0,76 млн.руб. и выше будет находиться в пределах от 5% до 35%.
Задание 4
Выпуск продукции по плану намечалось увеличить по сравнению с прошлым годом на 20%, фактическое увеличение составило 32%. Определите, на сколько процентов выполнен план по выпуску продукции?
Решение
Допустим, в прошлом году было выпущено 100 единиц продукции. Следовательно, план выпуска составил 120 единиц. Фактически было выпущено 132 единицы. Выполнение плана по выпуску продукции составило:
Задание 5
Количество тракторов на предприятии на 1 апреля 2012 г. составило 49 шт. В течение месяца произошли следующие изменения: 11 апреля поступило 3 трактора, 16 апреля выбыло 2. Определите среднее количество тракторов в апреле 2012 г.
Решение
Среднее количество тракторов определим как среднюю арифметическую взвешенную по формуле:
где n_i - количество тракторов в течение i-го периода; t_i - длина i-го периода.
| Период | Число тракторов n_i | Количество дней t_i | n_i\cdot t_i |
|---|---|---|---|
| 01.04-10.04 | 49 | 10 | 490 |
| 11.04-15.04 | 52 | 5 | 260 |
| 16.04-30.04 | 50 | 15 | 750 |
| Итого | 30 | 1500 |
Среднее количество тракторов в апреле 2012 г. - 50 штук.
Пользователь, раз уж ты добрался до этой строки, ты нашёл тут что-то интересное или полезное для себя. Надеюсь, ты просматривал сайт в браузере Firefox, который один правильно отражает формулы, встречающиеся на страницах. Если тебе понравился контент, помоги сайту материально. Отключи, пожалуйста, блокираторы рекламы и нажми на пару баннеров вверху страницы. Это тебе ничего не будет стоить, увидишь ты только то, что уже искал или ищешь, а сайту ты поможешь оставаться на плаву.