зевс охрана К работе агентства безопасности, как правило, предъявляются довольно высокие требования. Любую деятельность, которая направлена на организацию осуществления охраны и безопасности, необходимо выполнять максимально точно, вне зависимости от сложности. Специалисты, которые занимаются установкой систем сигнализации и видеонаблюдения в Одессе, должны учитывать все особенности территории, на которой происходит установка.

Задача 1

Решить графически задачу линейного программирования:

\left\lbrace\begin{array}{l}x_1+4x_2\le8\\3x_1-4x_2\le8\\x_1+4x_2\ge-11\\x_1\ge0\\x_2\ge0\end{array}\right.

Z=3x_1+x_2\to\max

Решение

Необходимо найти максимальное значение целевой функции Z=3x_1+x_2\to\max, при системе ограничений:

\left\lbrace\begin{array}{l}x_1+4x_2\le8\\3x_1-4x_2\le8\\x_1+4x_2\ge-11\\x_1\ge0\\x_2\ge0\end{array}\right.

Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).

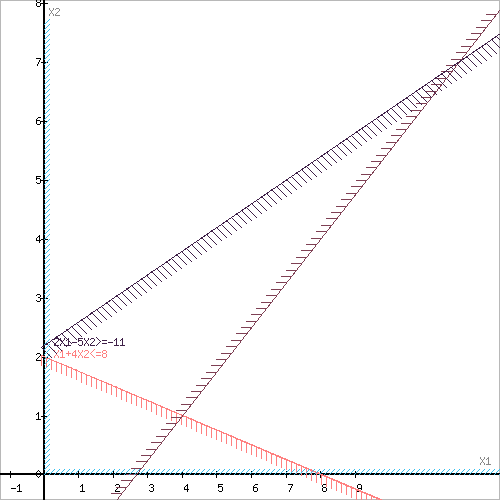
Границы области допустимых решений

Пересечением полуплоскостей будет являться область, координаты точек которой удовлетворяют условию - неравенствам системы ограничений задачи.

Обозначим границы области многоугольника решений.

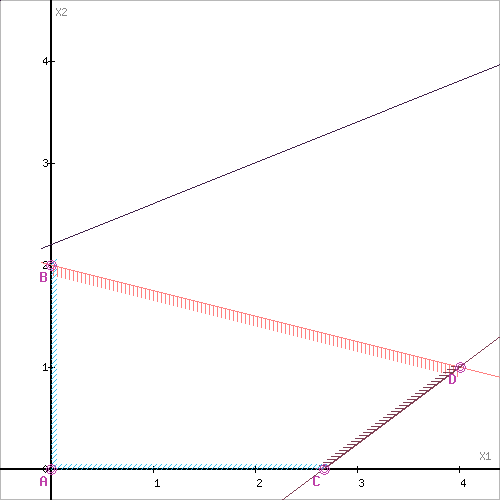
Рассмотрим целевую функцию задачи Z=3x_1+x_2\to\max.

Построим прямую, отвечающую значению функции: Z=0:\quad Z=3x_1+x_2=0. Будем двигать эту прямую параллельным образом. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией.

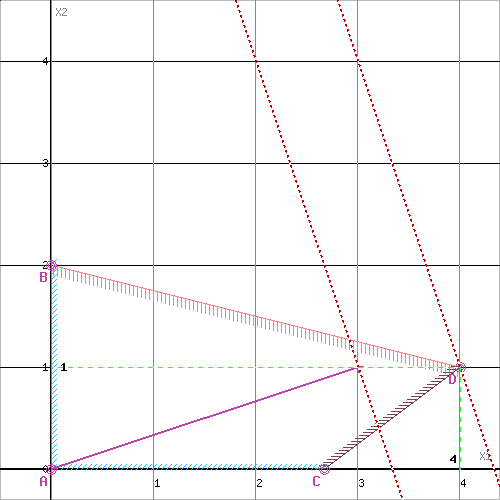
Равный масштаб

Область допустимых решений представляет собой многоугольник.

Прямая Z(x)={\rm}const пересекает область в точке D. Так как точка D получена в результате пересечения прямых x_1+4x_2=8 и 3x_1-4x_2=8, то ее координаты удовлетворяют решению системы уравнений

\left\lbrace\begin{array}{l}x_1+4x_2=8\\3x_1-4x_2=8\end{array}\right.

Решив систему уравнений, получим: x_1=4, x_2=1.

Откуда найдем максимальное значение целевой функции:

Z=3\cdot4+1\cdot1=13

Задача 2

Сельскохозяйственное предприятие планирует посадить некоторую сельскохозяйственную культуру двух сортов. Посевная площадь 1000 га. Сорта отличаются друг от друга требованиями к влаге во время вегетационного периода. Проанализировав погодные условия, выделены 4 состояния погоды (S1, S2, S3, S4), отличающиеся режимом осадков. Средняя урожайность (ц/га) каждого сорта на всем участке для каждого состояния погоды приведена в таблице:

	S1	S2	S3	S4
Сорт 1	27	33	35	41
Сорт 2	40	37	32	28

Возможные варианты посева:

А1 - сорт 1 посадить на 100% площади;

А2 - сорт 1 посадить на 75% площади, сорт 2 посадить на 25% площади;

А3 - сорт 1 посадить на 50% площади, сорт 2 посадить на 50% площади;

А4 - сорт 1 посадить на 25% площади, сорт 2 посадить на 75% площади;

А5 - сорт 2 посадить на 100% площади.

Определить оптимальную стратегию с помощью критериев недостаточного основания Лапласа, максиминного критерия Вальда, критерия минимаксного риска Сэвиджа, пессимизма-оптимизма Гурвица (коэффициент пессимизма взять равным 0,4).

Решение

Рассчитаем элементы матрицы полезности:

W_{11}=27\cdot1+40\cdot0=27;

W_{12}=33\cdot1+37\cdot0=33;

W_{13}=35\cdot1+32\cdot0=35;

W_{14}=41\cdot1+28\cdot0=41;

W_{21}=27\cdot0,75+40\cdot0,25=30,25;

W_{22}=33\cdot0,75+37\cdot0,25=34;

W_{23}=35\cdot0,75+32\cdot0,25=34,25;

W_{24}=41\cdot0,75+28\cdot0,25=37,75;

W_{31}=27\cdot0,5+40\cdot0,5=33,5;

W_{32}=33\cdot0,5+37\cdot0,5=35;

W_{33}=35\cdot0,5+32\cdot0,5=33,5;

W_{34}=41\cdot0,5+27\cdot0,5=34,5;

W_{41}=27\cdot0,25+40\cdot0,75=36,75;

W_{42}=33\cdot0,25+37\cdot0,75=36;

W_{43}=35\cdot0,25+32\cdot0,75=32,75;

W_{44}=41\cdot0,25+27\cdot0,75=31,25;

W_{51}=27\cdot0+40\cdot1=40;

W_{52}=33\cdot0+37\cdot1=37;

W_{53}=35\cdot0+32\cdot1=32;

W_{54}=41\cdot0+27\cdot1=28.

***Таблица урожайности***
	S1	S2	S3	S4
A1	27	33	35	41
A2	30,25	34	34,25	37,75
A3	33,5	35	33,5	34,5
A4	36,75	36	32,75	31,25
A5	40	37	32	28

Критерий недостаточного основания Лапласа

Если нет достаточных оснований считать, что вероятности того или иного спроса имеют неравномерное распределение, то они принимаются одинаковыми и задача сводится к поиску варианта, дающего

W=\max_{i=1..m}\biggl(\frac 1n\sum_{j=1}^n W_{ij}\biggr)

Рассчитаем средние значения элементов каждой строки

W_1=\frac{27+33+35+41}4=34;

W_2=\frac{30,25+34+34,25+37,75}4=34,0625;

W_3=\frac{33,5+35+33,5+34,5}4=34,125;

W_4=\frac{36,75+36+32,75+31,25}4=34,1875;

W_5=\frac{40+37+32+28}4=34,25.

***Результат вычислений***
	S1	S2	S3	S4	W_i
A1	27	33	35	41	34
A2	30,25	34	34,25	37,75	34,0625
A3	33,5	35	33,5	34,5	34,125
A4	36,75	36	32,75	31,25	34,1875
A5	40	37	32	28	34,25

Оптимальной по данному критерию является стратегия A5.

Максиминный критерий Вальда

Критерий Вальда обеспечивает выбор осторожной, пессимистической стратегии: для каждого решения A_i выбирается самая худшая ситуация (наименьшее из W_{ij}) и среди них отыскивается гарантированный максимальный эффект

W=\max_{i=1..m}\min_{j=1..n}W_{ij}

	S1	S2	S3	S4	min_i
A1	27	33	35	41	27
A2	30,25	34	34,25	37,75	30,25
A3	33,5	35	33,5	34,5	33,5
A4	36,75	36	32,75	31,25	31,25
A5	40	37	32	28	28

Оптимальной по данному критерию является стратегия A3.

Критерий минимаксного риска Сэвиджа

Суть этого критерия заключается в нахождении минимального риска. При выборе решения по этому критерию сначала матрице функции полезности (эффективности) сопоставляется матрица сожалений

D_{ij}=W_{ij}-\max_{i}W_{ij},

элементы которой отражают убытки от ошибочного действия, т.е. выгоду, упущенную в результате принятия i-го решения в j-м состоянии. Затем по матрице D выбирается решение по пессимистическому критерию Вальда, дающее наименьшее значение максимального сожаления.

D_{11}=41-27=14;

D_{12}=41-33=8;

D_{13}=41-35=6;

D_{14}=41-41=0;

D_{21}=37,75-30,25=7,5;

D_{22}=37,75-34=3,75;

D_{23}=37,75-34,25=3,5;

D_{24}=37,75-37,75=0;

D_{31}=35-33,5=1,5;

D_{32}=35-35=0;

D_{33}=35-33,5=1,5;

D_{34}=35-34,5=0,5;

D_{41}=36,75-36,75=0;

D_{42}=36,75-36=0,75;

D_{43}=36,75-32,75=4;

D_{44}=36,75-31,25=5,5;

D_{51}=40-40=0;

D_{52}=40-37=3;

D_{53}=40-32=8;

D_{54}=40-28=12.

***Матрица сожалений***
	S1	S2	S3	S4	max_i
A1	14	8	6	0	14
A2	7,5	3,75	3,5	0	7,5
A3	1,5	0	1,5	0,5	1,5
A4	0	0,75	4	5,5	5,5
A5	0	3	8	12	12

Минимальное значение у стратегии A3. Она является оптимальной.

Критерий пессимизма-оптимизма Гурвица

Ориентация на самый худший исход является своеобразной перестраховкой. Однако опрометчиво выбирать политику, которая излишне оптимистична. Критерий Гурвица предлагает некоторый компромисс:

W=\max_{i=1..m}\bigl[\alpha\cdot\max_{j=1..n}W_{ij}+(1-\alpha)\cdot\min_{j=1..n}W_{ij}\bigr]

где параметр \alpha принимает значение от 0 до 1 и выступает как коэффициент оптимизма.

Коэффициент пессимизма \alpha=0,4.

W_1=0,4\cdot41+(1-0,4)\cdot27=32,6;

W_2=0,4\cdot37,75+(1-0,4)\cdot30,25=33,25;

W_3=0,4\cdot35+(1-0,4)\cdot33,5=34,1;

W_4=0,4\cdot36,75+(1-0,4)\cdot31,25=34,35;

W_5=0,4\cdot40+(1-0,4)\cdot28=35,2.

Таблица расчетов
	S1	S2	S3	S4	Расчет
A1	27	33	35	41	32,6
A2	30,25	34	34,25	37,75	33,25
A3	33,5	35	33,5	34,5	34,1
A4	36,75	36	32,75	31,25	34,35
A5	40	37	32	28	35,2

Оптимальной по данному критерию является стратегия A5.

микротоки для лица

Пользователь, раз уж ты добрался до этой строки, ты нашёл тут что-то интересное или полезное для себя. Надеюсь, ты просматривал сайт в браузере Firefox, который один правильно отражает формулы, встречающиеся на страницах. Если тебе понравился контент, помоги сайту материально. Отключи, пожалуйста, блокираторы рекламы и нажми на пару баннеров вверху страницы. Это тебе ничего не будет стоить, увидишь ты только то, что уже искал или ищешь, а сайту ты поможешь оставаться на плаву.