Решение задач с использованием Microsoft Office для студентов 1 курса очно-заочного отделения
Содержание работы
Цель работы
Закрепление знаний и практических навыков работы на персональном компьютере с использованием современных компьютерных технологий.
Задания к контрольной работе
Контрольная работа состоит из четырех заданий, выполняемых в MS Office. Решение задач должно быть представлено в виде книги MS Excel и пояснительной записки, подготовленной в MS Word.
Задание 1. Протабулировать (вычислить) заданную функцию (таблица 1) на указанном диапазоне с шагом h. Построить график функции.
Задание 2. Найти сумму числового ряда и сравнить ее с точным решением, вычислив погрешности (таблица 2).
Задание 3. Найти корни уравнения (таблица 3), используя команду «Подбор параметра».
Задание 4. Описать технологию работы со списками в электронной таблице Excel (создания списка, сортировки, установки фильтрации, подведения промежуточных и общих итогов, создания сводной таблицы) в пояснительной записке в текстовом редакторе MS Word. Подготовить книгу Excel с примерами, демонстрирующими технологию работы со списками.
Варианты заданий на контрольную работу выдаются преподавателем.
При работе над заданием рекомендуется использовать литературу по MS Office и систему помощи (справки) по MS Office.
Требования к представлению и оформлению контрольной работы
Работа должна быть представлена на бумажном (пояснительная записка) и электронном (в виде файлов на дискете) носителях. Пояснительная записка должна быть отпечатана на стандартных листах формата А4 (210×297 мм). На дискете должны быть документы в форматах MS Word (пояснительная записка) и MS Excel (рабочая книга, содержащая листы с четырьмя решенными заданиями). При необходимости файлы могут быть заархивированы.
Текст пояснительной записки должен быть набран с учетом следующих параметров: поля документа сверху - 2,5 см, снизу - 2,5 см, слева - 3,0 см, справа - 1,5 см, шрифт Times New Roman, размер шрифта 14, межстрочный интервал 1, выравнивание - по ширине страницы, автоматическая нумерация страниц. Рисунки и таблицы должны иметь поясняющие надписи и быть пронумерованы.
Содержание пояснительной записки:
- титульный лист (см. образец);
- лист содержания (оглавление должно составляться с использованием средств автоматизации MS Word);
- основная часть, включающая четыре раздела в каждом из которых приводится постановка задачи и описание ее решения, сопровождаемое необходимыми иллюстрациями;
- список литературы (перечень использованных при выполнении контрольной работы материалов, на которые должны быть ссылки в тексте).
При оформлении листов рабочей книги MS Excel необходимо использовать возможности форматирования и защиты данных (заголовков таблиц, формул и т.п.) от изменений.
При оформлении работы студент должен показать владение технологиями работы с пакетом MS Office (MS Word и MS Excel).
Срок выполнения
Задание должно быть представлено в деканат очно-заочного отделения за месяц до начала установочной сессии.
Порядок защиты работы
- Получить рецензию на работу в деканате.
- Устранить отмеченные недостатки.
- К защите обязательно представить пояснительную записку и электронную версию работы.
- Работа защищается с использованием компьютера (студент демонстрирует полученные знания и практические навыки работы на компьютере, отвечая на вопросы преподавателя, принимающего контрольную работу).
- По результатам защиты выставляется зачет за контрольную работу.
Варианты заданий к задаче 1
| № варианта | Уравнения | Отрезок, содержащий корень | Шаг |
|---|---|---|---|
| 1 | 3\sin\sqrt{x}+0,35x-3,8=y | [2; 3] | 0,1 |
| 2 | 0,25x^3+x-1,2502=y | [0; 2] | 0,2 |
| 3 | x+\sqrt{x}+\sqrt[3]{x}-2,5=y | [0,4; 1] | 0,05 |
| 4 | x-\frac{1}{(3+\sin{3,6x})}=y | [0; 0,85] | 0,05 |
| 5 | 0,1x^2-x\ln x=y | [1; 2] | 0,1 |
| 6 | tg\ x-\frac{1}{3}tg^3x+\frac{1}{5}tg^5x-\frac{1}{3}=y | [0; 0,8] | 0,05 |
| 7 | \arccos x-\sqrt{1-0,3x^3}=y | [0; 1] | 0,1 |
| 8 | 3x-4\ln x-5=y | [2; 4] | 0,2 |
| 9 | \cos\frac{2}{x}-2\sin\frac{1}{x}+\frac{1}{x}=y | [1; 2] | 0,1 |
| 10 | \sqrt{1-0,4x^2}-\arcsin x=y | [0; 1] | 0,1 |
| 11 | e^x-e^{-x}-2=y | [0; 1] | 0,1 |
| 12 | \sin(\ln x)-\cos(\ln x)+2\ln x=y | [1; 3] | 0,2 |
| 13 | x-2+\sin\frac{1}{x}=y | [1,2; 2] | 0,08 |
| 14 | e^x+\ln x-10x=y | [3; 4] | 0,1 |
| 15 | \cos x-e^{-\frac{x^2}{2}}+x-1=y | [1; 2] | 0,1 |
| 16 | 1-x+\sin x-\ln(1+x)=y | [0; 1,5] | 0,15 |
| 17 | 3x-14+e^x-e^{-x}=y | [1; 3] | 0,2 |
| 18 | \sqrt{1-x}-tg\ x=y | [0; 1] | 0,1 |
| 19 | x+\cos{(0,52x+2)}=y | [0,5; 1] | 0,05 |
| 20 | 3\ln(2x)+6\ln x-5=y | [1; 3] | 0,2 |
| 21 | \sin{x^2}+\cos{x^2}-10x=y | [0; 1] | 0,1 |
| 22 | x^2-\ln(1+x)-3=y | [2; 3] | 0,1 |
| 23 | 2x\sin x-\cos x=y | [0,4; 1] | 0,05 |
| 24 | e^x+\sqrt{1+e^{2x}}-2=y | [-1; 0] | 0,1 |
| 25 | \ln x-x+1,8=y | [2; 3] | 0,1 |
| 26 | x\ tg\ x-\frac{1}{3}=y | [0,2; 1] | 0,05 |
| 27 | tg\frac{x}{2}-ctg\frac{x}{2}+x=y | [1; 2] | 0,1 |
| 28 | 0,4+arctg\sqrt{x}-x=y | [1; 2] | 0,1 |
| 29 | \sqrt{1-x}-\cos\sqrt{1-x}=y | [0; 1] | 0,1 |
| 30 | 0,6\cdot3^x-2,3x-3=y | [2; 3] | 0,1 |
Варианты заданий к задаче 2
| № варианта | Сумма ряда | Точное решение |
|---|---|---|
| 1 | \sum\limits_{k=1}^M\frac{(k+1)^3}{k!};\ M=10 | 15e |
| 2 | \sum\limits_{k=1}^M\frac{k^n}{k!};\ n=4,\ M=12 | 15e |
| 3 | \sum\limits_{k=1}^M\frac{k!}{(n+k-1)!};\ n=5,\ M=8 | \frac{1}{(n-2)(n-1)!} |
| 4 | \sum\limits_{k=0}^M\frac{(-1)^k}{k!(k+1)!};\ M=10 | 0,476725 |
| 5 | \sum\limits_{k=1}^M\frac{(-1)^{k+1}}{(2k-1)2k(2k+1)!};\ M=10 | \frac{1}{2}(1-\ln2) |
| 6 | \sum\limits_{k=1}^M(-1)^{k+1}\frac{1}{(3k-2)};\ M=10 | \frac{1}{3}\left(\frac{\pi}{3}+\ln2\right) |
| 7 | \sum\limits_{k=1}^M\frac{1}{(8k-1)(8k+1)};\ M=12 | \frac{1}{2}-\frac{\pi}{16}\left(\sqrt{2}+1\right) |
| 8 | \sum\limits_{k=1}^M\frac{1}{2^k\ k};\ M=12 | \ln2 |
| 9 | \sum\limits_{k=1}^M\frac{1}{2^k\ k^2};\ M=8 | \frac{\pi^2}{12}-\frac{1}{2}\left(\ln2\right)^2 |
| 10 | \sum\limits_{k=0}^M(-1)^k\frac{1}{n^{2n}};\ n=3,\ M=10 | \frac{n^2}{n^2+1} |
| 11 | \sum\limits_{k=0}^M\frac{1}{k!};\ M=8 | e |
| 12 | \sum\limits_{k=0}^M\frac{(-1)^k}{k!};\ M=10 | \frac{1}{e} |
| 13 | 2\sum\limits_{k=1}^M\frac{k}{(2k+1)!};\ M=8 | \frac{1}{e} |
| 14 | \sum\limits_{k=1}^M\frac{k}{(k+1)!};\ M=10 | 1 |
| 15 | \sum\limits_{k=0}^M\frac{1}{(2k)!};\ M=8 | \frac{1}{2}\left(e+\frac{1}{e}\right) |
| 16 | \sum\limits_{k=0}^M\frac{(-1)^k}{(2k)!};\ M=8 | \cos1 |
| 17 | \sum\limits_{k=0}^M\frac{1}{(2k+1)!};\ M=10 | \frac{1}{2}\left(e-\frac{1}{e}\right) |
| 18 | \sum\limits_{k=1}^M\frac{(-1)^{k-1}}{(2k-1)!};\ M=8 | \sin1 |
| 19 | \sum\limits_{k=0}^{M}aq^k;\ a=2,7;\ q=0,5;\ M=12 | \frac{a}{1-q} |
| 20 | \sum\limits_{k=1}^M(-1)^{k+1}\frac{1}{k^2};\ M=14 | \frac{\pi}{2} |
| 21 | \sum\limits_{k=1}^M\frac{(-1)^{k+1}}{(2k-1)^3};\ M=14 | \frac{\pi}{32} |
| 22 | \sum\limits_{k=0}^{M}(a+kr)q^k;\ a=3,7;\ r=1,1;\ q=-0,5;\ M=12 | \frac{a}{1-q}+\frac{rq}{(1-q)^2} |
| 23 | \sum\limits_{k=1}^M(-1)^{k+1}\frac{k}{(k+1)^2};\ M=15 | \frac{\pi^2}{12}-\ln2 |
| 24 | \sum\limits_{k=1}^M(-1)^{k+1}\frac{1}{3k-2};\ M=16 | \frac{1}{3}\left(\frac{\pi}{\sqrt{3}}+\ln2\right) |
| 25 | \sum\limits_{k=1}^M(-1)^{k+1}\frac{1}{3k-1};\ M=14 | \frac{1}{3}\left(\frac{\pi}{\sqrt{3}}-\ln2\right) |
| 26 | \sum\limits_{k=1}^M(-1)^{k+1}\frac{1}{4k-3};\ M=16 | \frac{1}{4\sqrt{2}}\left[\pi+2\ln\left(\sqrt{2}+1\right)\right] |
| 27 | \sum\limits_{k=0}^M\frac{(-1)^k}{(k!)^2};\ M=8 | 0,223891 |
| 28 | \sum\limits_{k=0}^M\frac{(-1)^k}{k!(k+1)!};\ M=10 | 0,576725 |
| 29 | \sum\limits_{k=1}^M\frac{(-1)^k}{(2k-1)2^{2k-1}};\ M=8 | arctg(2)-\frac{\pi}{2} |
| 30 | \sum\limits_{k=1}^M\frac{k^2}{k!};\ M=10 | 2e |
Варианты заданий к задаче 3
| № варианта | Уравнения | Отрезок, содержащий корень | Приближенное значение |
|---|---|---|---|
| 1 | 1-x+\sin x-\ln(1+x)=0 | [0; 1,5] | 1,1474 |
| 2 | 3x-14+e^x-e^{-x}=0 | [1; 3] | 2,0692 |
| 3 | \sqrt{1-x}-tg\ x=0 | [0; 1] | 0,5768 |
| 4 | x+\cos(x^{0,52}+2)=0 | [0,5; 1] | 0,9892 |
| 5 | 3\ln^2x+6\ln x-5=0 | [1; 3] | 1,8832 |
| 6 | \sin{x^2}+\cos{x^2}-10x=0 | [0; 1] | 0,1010 |
| 7 | x^2-\ln(1+x)-3=0 | [2; 3] | 2,0267 |
| 8 | 2x\sin x-\cos x=0 | [0,4; 1] | 0,6533 |
| 9 | e^x+\sqrt{1+e^{2x}}-2=0 | [-1; 0] | -0,2877 |
| 10 | \ln x-x+1,8=0 | [2; 3] | 2,8459 |
| 11 | x\ tg\ x-\frac{1}{3}=0 | [0,2; 1] | 0,5472 |
| 12 | tg\frac{x}{2}-ctg\frac{x}{2}+x=0 | [1; 2] | 1,0769 |
| 13 | 0,4+arctg\sqrt{x}-x=0 | [1; 2] | 1,2388 |
| 14 | \sqrt{1-x}-\cos\sqrt{1-x}=0 | [0; 1] | 0,4538 |
| 15 | 0,6\cdot3^x-2,3x-3=0 | [2; 3] | 2,4200 |
| 16 | 3\sin\sqrt{x}+0,35x-3,8=0 | [2; 3] | 2,2985 |
| 17 | 0,25x^3+x-1,2502=0 | [0; 2] | 1,0001 |
| 18 | x+\sqrt{x}+\sqrt[3]{x}-2,5=0 | [0,4; 1] | 0,7376 |
| 19 | x-\frac{1}{3+\sin{3,6x}}=0 | [0; 0,85] | 0,2624 |
| 20 | 0,1x^2-x\ln x=0 | [1; 2] | 1,1183 |
| 21 | tg\ x-\frac{1}{3}tg^3x+\frac{1}{5}tg^5x-\frac{1}{3}=0 | [0; 0,8] | 0,3333 |
| 22 | arccos\ x-\sqrt{1-0,3x^3}=0 | [0; 1] | 0,5629 |
| 23 | 3x-4\ln x-5=0 | [2; 4] | 3,2300 |
| 24 | \cos\frac{2}{x}-2\sin\frac{1}{x}+\frac{1}{x}=0 | [1; 2] | 1,8756 |
| 25 | \sqrt{1-0,4x^2}-arcsin\ x=0 | [0; 1] | 0,7672 |
| 26 | e^x-e^{-x}-2=0 | [0; 1] | 0,8814 |
| 27 | \sin(\ln x)-\cos(\ln x)+2\ln x=0 | [1; 3] | 1,3749 |
| 28 | x-2+\sin\frac{1}{x}=0 | [1,2; 2] | 1,3077 |
| 29 | e^x+\ln x-10x=0 | [3; 4] | 3,5265 |
| 30 | \cos x-e^{-\frac{x^2}{2}}+x-1=0 | [1; 2] | 1,0804 |
Пояснения к задаче 1
Рассмотрим процедуру построения графика функции Y=\cos^2(\pi x) при x\in[0;\ 1].
Для построения графика функции необходимо сначала построить таблицу ее значений при различных значениях аргумента, причем аргумент изменяется с фиксированным шагом. Будем считать, что шаг h = 0,1.
Необходимо создать первый столбец х: 0; 0,1; 0,2; 0,3; ...; 1 и второй столбец y = f(x): y(0), y(0,1), y(0,2), ..., y(1). В создании столбцов Вам поможет приведенная ниже таблица.
| Ячейка | Величина | Значение или формула |
|---|---|---|
В1 |
h - шаг | 0,1 |
В4 |
Нижняя граница диапазона x | 0 |
В5 |
Следующее значение по x вычисляем формулой | =В4+$В$1 |
В6:В14 |
Значения переменной x на заданном диапазоне | Копируем ячейку В5 на диапазон В6:В14 |
С4 |
Значение функции y в точке х = 0 (используйте Мастер функций) | =COS(ПИ()*В4)^2 |
С5:С14 |
Значения функции y на заданном диапазоне | Копируем ячейку С4 на диапазон С5:С14 |
С помощью Мастера диаграмм построить диаграмму типа
точечная «график» (исходные данные - диапазон В4:С14),
указав при этом, что метками оси Х являются значения первого столбца (В4:В14).
Результат показан на рис.1.
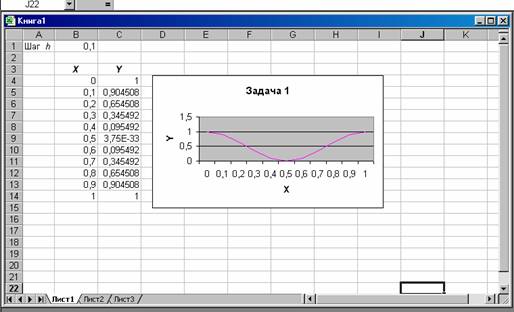
Рис.1. Решение задачи 1
Пояснения к задаче 2
Аналогично задаче 1 получаем первый столбец значений K,
где 1 ≤ K ≤ N, и столбец f(K).
Значение суммы можно получить, например, по формуле: =СУММ(С5:С14),
где С5:С14 - диапазон ячеек столбца f(K), а
ячейка С15 содержит формулу суммы.
Погрешности вычисляются по формулам: \Delta=\frac{S}{T} и \Psi=\frac{\Delta}{T}. Здесь Δ - абсолютная погрешность, S - сумма ряда, T - точное значение суммы, Ψ - относительная погрешность.
Пример решения задачи 2 показан на рис.2.
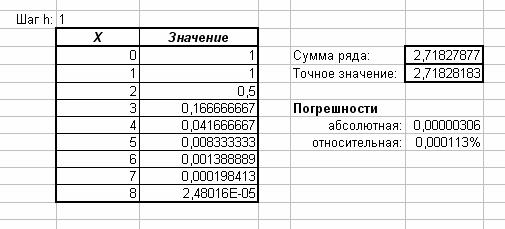
Рис.2. Решение задачи 2
Пояснения к задаче 3
Найти корни уравнения (полинома) x^3-0,01x^2-0,7044x+0,139104=0.
У полинома третьей степени три корня. Для нахождения корней
их нужно предварительно локализовать. С этой целью необходимо построить
график функции или ее протабулировать. Протабулируем полином на отрезке
[-1; 1] с шагом 0,2. Результат приведен на рисунке 2, где в ячейку В2
введена формула =А2^3-0,01*A2^2-0,7044*A2+0,139104.
Из рис.3 видно, что полином меняет знак на интервалах: [-1; -0,8], [0,2; 0,4], [0,6; 0,8]. Это означает, что на каждом из них имеется корень данного полинома. Таким образом, мы локализовали все три вещественных корня нашего полинома.
Найдем корни полинома методом последовательных приближений с помощью команды Сервис меню Подбор параметра. Относительная погрешность вычислений и предельное число итераций задаются на вкладке Вычисления диалогового окна Параметры, открываемого командой Сервис, Параметры.
Зададим относительную погрешность и предельное число
итераций равными 0,00001 и 1000 соответственно. В качестве начальных
приближений можно взять любые точки из отрезков локализации корней.
Возьмем, например, их средние точки: -0,9; 0,3 и 0,7 и введем их в
диапазон ячеек C2:C4. В ячейки D2:D4 скопируем
ячейку В2. Таким образом, в ячейках D2:D4
вычисляются значения полинома при значениях аргумента, введенного в
ячейки С2:С4 соответственно.
Теперь выберем команду Сервис, Подбор параметра и заполним диалоговое окно Подбор параметра:
| Установить в ячейке: | $D$2 |
| Значение | 0 |
| Изменяя значение ячейки | $C$2 |
Вводить ссылки на ячейки надо не с клавиатуры, а указателем мыши.
После нажатия кнопки OK средство подбора параметров
находит приближенное значение корня, которое помещает в ячейку С2.
В данном случае оно равно -0,919999.
Аналогично в ячейках С3 и С4
находим два оставшихся корня. Они равны 0,20999 и 0,71999.
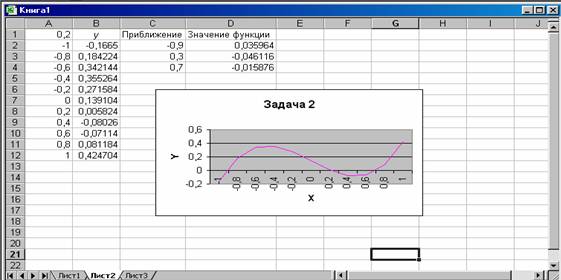
Рис.3. Окно исходной информации для решения задачи 3
Замечание. В Вашем случае (таблица 3) решается трансцендентное уравнение, которое имеет единственный корень на заданном отрезке. Поэтому локализация корней не требуется.
Пояснения к задаче 4
Для демонстрации возможностей работы со списками в электронной таблице MS Excel необходимо подготовить примеры и разместить их на листе рабочей книги. На рис.4-9 показаны фрагменты таблиц на тему «Автокаталог».
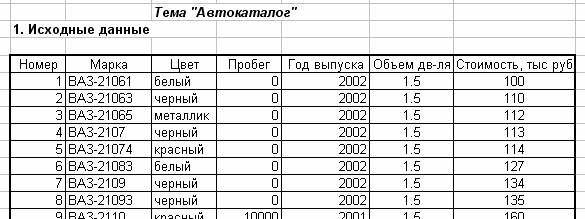
Рис.4. Таблица с исходным списком
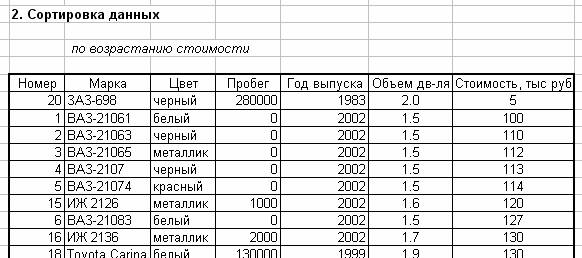
Рис.5. Таблица после сортировки
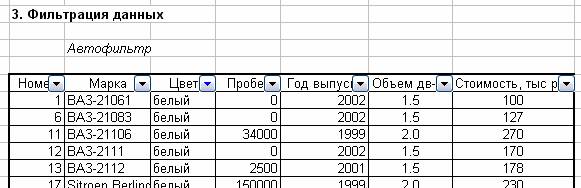
Рис.6. Использование фильтра
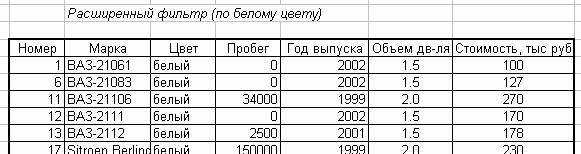
Рис.7. Использование расширенного фильтра
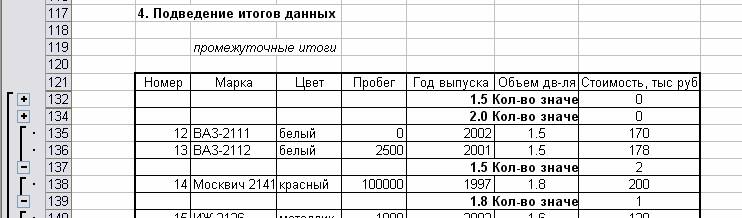
Рис.8. Подведение итогов
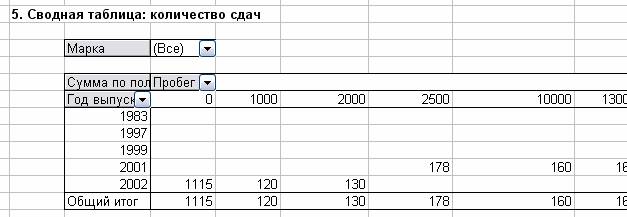
Рис.9. Сводная таблица
Образец оформления титульного листа пояснительной записки к контрольной работе

Пироги по акции с доставкои по спб заказать пироги.
Пользователь, раз уж ты добрался до этой строки, ты нашёл тут что-то интересное или полезное для себя. Надеюсь, ты просматривал сайт в браузере Firefox, который один правильно отражает формулы, встречающиеся на страницах. Если тебе понравился контент, помоги сайту материально. Отключи, пожалуйста, блокираторы рекламы и нажми на пару баннеров вверху страницы. Это тебе ничего не будет стоить, увидишь ты только то, что уже искал или ищешь, а сайту ты поможешь оставаться на плаву.