I. Задания для выполнения контрольной работы
II. Задания для выполнения лабораторной работы
III. Дополнительные варианты задач для выполнения лабораторной работы
I. Задания для выполнения контрольной работы
I.1. Порядок оформления контрольной работы
Контрольная работа выполняется и защищается в установленные деканатом сроки.
Титульный лист контрольной работы должен содержать все необходимые реквизиты: названия института и факультета; наименование учебной дисциплины; номер группы и номер зачетной книжки, Ф.И.О. студента и преподавателя.
Работа без указания номера зачетной книжки и номера группы проверке не подлежит, при отсутствии Ф.И.О. преподавателя установленные сроки проверки работы могут быть нарушены.
Решение задач контрольной работы должно сопровождаться необходимыми комментариями, т.е. все основные моменты процесса решения задачи должны быть раскрыты и обоснованы на основе соответствующих теоретических положений. Для решения задач допустимо использование средств Excel.
К собеседованию допускаются студенты, выполнившие правильно и в полном объеме все задания контрольной работы.
Для получения зачета по результатам собеседования студент должен знать теоретические основы тематики задач контрольной работы и уметь ответить на конкретные вопросы по содержанию проверенной работы.
Номер вашего варианта соответствует последней цифре зачетной книжки (если преподавателем не задан другой порядок выбора варианта).
I.2. Задачи
Задача 1
Решить графическим методом типовую задачу оптимизации
1.1. Инвестор, располагающий суммой в 300 тыс. ден. ед., может вложить свой капитал в акции автомобильного концерна А и строительного предприятия В. Чтобы уменьшить риск, акций А должно быть приобретено на сумму по крайней мере в два раза большую, чем акций В, причем последних можно купить не более чем на 100 тыс. ден. ед.
Дивиденды по акциям А составляют 8% в год, по акциям В - 10%. Какую максимальную прибыль можно получить в первый год?
Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на минимум, и почему?
1.2. Совхоз для кормления животных использует два вида корма. В дневном рационе животного должно содержаться не менее 6 единиц питательного вещества А и не менее 12 единиц питательного вещества В. Какое количество корма надо расходовать ежедневно на одно животное, чтобы затраты были минимальными? Использовать данные таблицы.
| Питательное вещество | Количество питательных веществ в 1 кг корма | |
|---|---|---|
| 1 | 2 | |
| А | 2 | 1 |
| В | 2 | 4 |
| Цена 1 кг корма, тыс. руб. | 0,2 | 0,3 |
Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на максимум, и почему?
1.3. Некоторая фирма выпускает дна набора удобрений для газонов: обычный и улучшенный. В обычный набор входит 3 кг азотных, 4 кг фосфорных и 1 кг калийных удобрений, а в улучшенный - 2 кг азотных, 6 кг фосфорных и 3 кг калийных удобрений. Известно, что для некоторого газона требуется но меньшей мере 10 кг азотных, 20 кг фосфорных и 7 кг калийных удобрений. Обычный набор стоит 3 ден. ед., а улучшенный - 4 ден. ед. Какие и сколько наборов удобрений нужно купить, чтобы обеспечить эффективное питание почвы и минимизировать стоимость?
Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на максимум, и почему?
1.4. На имеющихся у фермера 400 га земли он планирует посеять кукурузу и сою. Сев и уборка кукурузы требуют на каждый гектар 200 ден. ед. затрат, а сои - 100 ден. ед. На покрытие расходов, связанных с севом и уборкой, фермер получил ссуду в 60 тыс. ден. ед. Каждый гектар, засеянный кукурузой, принесет 30 центнеров, а каждый гектар, засеянный соей, - 60 центнеров. Фермер заключил договор на продажу, по которому каждый центнер кукурузы принесет ему 3 ден. ед., а каждый центнер сои - 6 ден. ед. Однако согласно этому договору фермер обязан хранить убранное зерно в течение нескольких месяцев на складе, максимальная вместимость которого равна 21 тыс. центнеров.
Фермеру хотелось бы знать, сколько гектаров нужно засеять каждой из этих культур, чтобы получить максимальную прибыль.
Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на минимум, и почему?
1.5. Продукция двух видов (краска для внутренних (I) и наружных (Е) работ) поступает в оптовую продажу. Для производства красок используются два исходных продукта - A и В. Максимально возможные суточные запасы этих продуктов составляют 6 и 8 тонн соответственно. Расходы продуктов А и В на 1 т соответствующих красок приведены в таблице.
| Исходный продукт | Расход исходных продуктов на тонну краски, т | Максимально возможный запас, т | |
|---|---|---|---|
| Краска Е | Краска I | ||
| А | 1 | 2 | 6 |
| В | 2 | 1 | 8 |
Изучение рынка сбыта показало, что суточный спрос на краску I никогда не превышает спроса на краску Е более чем на 1 т. Кроме того, установлено, что спрос на краску I никогда не превышает 2 т в сутки. Оптовые цены одной тонны красок равны 3000 ден. ед. для краски Е и 2000 ден. ед. для краски I. Какое количество краски каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным?
Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на минимум, и почему?
1.6. Финансовый консультант фирмы «ABC» консультирует клиента по оптимальному инвестиционному портфелю. Клиент хочет вложить средства (не более 25 000 долл.) в два наименования акций крупных предприятий в составе холдинга «Дикси». Анализируются акции «Дикси - Е» и «Дикси - B». Цены на акции: «Дикси - Е» - 5 долл. за акцию; «Дикси - В» - 3 долл. за акцию.
Клиент уточнил, что он хочет приобрести максимум 6000 акций обоих наименований, при этом акций одного из наименований должно быть не более 5000 штук.
По оценкам «ABC», прибыль от инвестиций в эти акции в следующем году составит: «Дикси - Е» - 1,1 долл.; «Дикси - B» - 0,9 долл.
Задача консультанта состоит в том, чтобы выдать клиенту рекомендации по оптимизации прибыли от инвестиций.
Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на минимум, и почему?
1.7. Завод - производитель высокоточных элементов для автомобилей выпускает два различных типа деталей – Х и У. Завод располагает фондом рабочего времени в 4000 чел.-ч в неделю. Для производства одной детали типа X требуется 1 чел.-ч, а для производства одной детали типа Y- 2 чел.-ч. Производственные мощности завода позволяют выпускать максимум 2250 деталей типа X и 1750 деталей типа Y в неделю. Каждая деталь типа X требует 2 кг металлических стержней и 5 кг листового металла, а для производства одной детали типа Y необходимо 5 кг металлических стержней и 2 кг листового металла. Уровень запасов каждого вида металла составляет 10000 кг в неделю. Кроме того, еженедельно завод поставляет 600 деталей типа X своему постоянному заказчику. Существует также профсоюзное соглашение, в соответствии с которым общее число производимых в течение одной недели деталей должно составлять не менее 1500 штук.
Сколько деталей каждого типа следует производить, чтобы максимизировать общий доход за неделю, если доход от производства одной детали типа X составляет 30 ден. ед., а от производства одной детали типа Y - 40 ден. ед.?
Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на минимум, и почему?
1.8. Имеется два вида корма I и II, содержащие питательные вещества (витамины) S1, S2 и S3 Содержание числа единиц питательных веществ в 1 кг каждого вида корма и необходимый минимум питательных веществ приведены в таблице.
| Питательное вещество (витамин) | Необходимый минимум питательных веществ | Число единиц питательных веществ в 1 кг корма | |
|---|---|---|---|
| I | II | ||
| S1 | 9 | 3 | 1 |
| S2 | 8 | 1 | 2 |
| S3 | 12 | 1 | 6 |
Стоимость 1 кг корма I и II соответственно равна 4 и 6 ден. ед.
Необходимо составить дневной рацион, имеющий минимальную стоимость, в котором содержание, питательных веществ каждого вида было бы не менее установленного предела.
Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на максимум, и почему?
1.9. При производстве двух видов продукции используется 4 типа ресурсов. Норма расхода ресурсов на производство единицы продукции, общий объем каждого ресурса заданы в таблице.
| Ресурсы | Норма затрат ресурсов на товары | Общее количество ресурсов | |
|---|---|---|---|
| 1-го вида | 2-го вида | ||
| 1 | 2 | 2 | 12 |
| 2 | 1 | 2 | 8 |
| 3 | 4 | 0 | 16 |
| 4 | 0 | 4 | 12 |
Прибыль от реализации одной единицы продукции первого вида составляет 2 ден. ед., второго вида - 3 ден. ед.
Задача состоит в формировании производственной программы выпуска продукции, обеспечивающей максимальную прибыль от ее реализации.
Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на минимум, и почему?
1.10. Фирма производит два широко популярных безалкогольных напитка - «Лимонад» и «Тоник». Фирма может продать всю продукцию, которая будет произведена. Однако объем производства ограничен количеством основного ингредиента и производственной мощностью имеющегося оборудования. Для производства 1 л «Лимонада» требуется 0,02 ч работы оборудования, а для производства 1 л «Тоника» - 0,04 ч. Расход специального ингредиента составляет 0,01 кг и 0,04 кг на 1 л «Лимонада» и «Тоника» соответственно. Ежедневно в распоряжении фирмы имеется 24 ч времени работы оборудования и 16 кг специального ингредиента. Прибыль фирмы составляет 0,10 ден. ед. за 1 л «Лимонада» и 0,30 ден. ед. за 1 л «Тоника». Сколько продукции каждого вида следует производить ежедневно, если цель фирмы состоит в максимизации ежедневной прибыли?
Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на минимум, и почему?
Задача 2
Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования1
2.1. Для изготовления четырех видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и цены реализации единицы каждого вида продукции приведены в таблице.
| Тип сырья | Нормы расхода сырья на одно изделие | Запасы сырья | |||
|---|---|---|---|---|---|
| А | Б | В | Г | ||
| I | 1 | 2 | 1 | 0 | 18 |
| II | 1 | 1 | 2 | 1 | 30 |
| III | 1 | 3 | 3 | 2 | 40 |
| Цена изделия | 12 | 7 | 18 | 10 | |
Требуется:
- Сформулировать прямую оптимизационную задачу на максимум выручки от реализации готовой продукции, получить оптимальный план выпуска продукции.
- Сформулировать двойственную задачу и найти ее оптимальный план с помощью теорем двойственности.
- Пояснить нулевые значения переменных в оптимальном плане.
- На основе свойств двойственных оценок и теорем двойственности:
- проанализировать использование ресурсов в оптимальном плане исходной задачи;
- определить, как изменятся выручка и план выпуска продукции при увеличении запасов сырья I и II видов на 4 и 3 единицы соответственно и уменьшении на 3 единицы сырья III вида;
- оценить целесообразность включения в план изделия Д ценой 10 ед., на изготовление которого расходуется по две единицы каждого вида сырья.
2.2. Для изготовления четырех видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и цены реализации единицы каждого вида продукции приведены в таблице.
| Тип сырья | Нормы расхода сырья на одно изделие | Запасы сырья | |||
|---|---|---|---|---|---|
| А | Б | В | Г | ||
| I | 1 | 0 | 2 | 1 | 180 |
| II | 0 | 1 | 3 | 2 | 210 |
| III | 4 | 2 | 0 | 4 | 800 |
| Цена изделия | 9 | 6 | 4 | 7 | |
Требуется:
- Сформулировать прямую оптимизационную задачу на максимум выручки от реализации готовой продукции, получить оптимальный план выпуска продукции.
- Сформулировать двойственную задачу и найти ее оптимальный план с помощью теорем двойственности.
- Пояснить нулевые значения переменных в оптимальном плане.
- На основе свойств двойственных оценок и теорем двойственности:
- проанализировать использование ресурсов в оптимальном плане исходной задачи;
- определить, как изменятся выручка и план выпуска продукции при увеличении запасов сырья II и III видов на 120 и 160 единиц соответственно и уменьшении на 60 единиц запасов сырья I вида;
- оценить целесообразность включения в план изделия Д ценой 12 единиц, на изготовление которого расходуется по две единицы каждого вида сырья.
2.3. Для изготовления четырех видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и цены реализации единицы каждого вида продукции приведены в таблице.
| Тип сырья | Нормы расхода сырья на одно изделие | Запасы сырья | |||
|---|---|---|---|---|---|
| А | Б | В | Г | ||
| I | 2 | 1 | 3 | 2 | 200 |
| II | 1 | 2 | 4 | 8 | 160 |
| III | 2 | 4 | 1 | 1 | 170 |
| Цена изделия | 5 | 7 | 3 | 6 | |
Требуется:
- Сформулирован, прямую оптимизационную задачу на максимум выручки от реализации ГОТОВОЙ продукции, получить оптимальный план выпуска продукции.
- Сформулировать двойственную задачу и найти ее оптимальный план с помощью теорем двойственности.
- Пояснить нулевые значения переменных в оптимальном плане.
- На основе свойств двойственных оценок и теорем двойственности:
- проанализировать использование ресурсов в оптимальном плане исходной задачи;
- определить, как изменятся выручка от реализации продукции и план ее выпуска при увеличении запасов сырья I и II видов на 8 и 10 единиц соответственно и уменьшении на 5 единиц запасов сырья III вида;
- оценить целесообразность включения в план изделия Д ценой 10 единиц, на изготовление которого расходуется по две единицы каждого вида сырья.
2.4. Для изготовления трех видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и цены реализации единицы каждого вида продукции приведены в таблице.
| Тип сырья | Нормы расхода сырья на одно изделие | Запасы сырья | ||
|---|---|---|---|---|
| А | Б | В | ||
| I | 4 | 2 | 1 | 180 |
| II | 3 | 1 | 2 | 210 |
| III | 1 | 2 | 3 | 244 |
| Цена изделия | 10 | 14 | 12 | |
Требуется:
- Сформулировать прямую оптимизационную задачу на максимум выручки от реализации готовой продукции, получить оптимальный план выпуска продукции. ,
- Сформулировать двойственную задачу и найти ее оптимальный план с помощью теорем двойственности.
- Пояснить нулевые значения переменных в оптимальном плане.
- На основе свойств двойственных оценок и теорем двойственности:
- проанализировать использование ресурсов в оптимальном плане исходной задачи;
- определить, как изменятся выручка от реализации продукции и план ее выпуска при увеличении запасов сырья I и III видов на 4 единицы каждого;
- оценить целесообразность включения в план изделия Г ценой 13 единиц, на изготовление которого расходуется соответственно 1, 3 и 2 единицы каждого вида сырья, и изделия Д ценой 12 единиц, на изготовление которого расходуется по две единицы каждого вида сырья.
2.5. На основании информации, приведенной в таблице, решается задача оптимального использования ресурсов на максимум выручки от реализации готовой продукции.
| Вид ресурсов | Нормы расхода ресурсов на ед. продукции | Запасы ресурсов | ||
|---|---|---|---|---|
| I вид | II вид | III вид | ||
| Труд | 1 | 4 | 3 | 200 |
| Сырье | 1 | 1 | 2 | 80 |
| Оборудование | 1 | 1 | 2 | 140 |
| Цена изделия | 40 | 60 | 80 | |
Требуется:
- Сформулировать прямую оптимизационную задачу на максимум выручки от реализации готовой продукции, получить оптимальный план выпуска продукции.
- Сформулировать двойственную задачу и найти ее оптимальный план с помощью теорем двойственности.
- Пояснить нулевые значения переменных в оптимальном плане.
- На основе свойств двойственных оценок и теорем двойственности:
- проанализировать использование ресурсов в оптимальном плане исходной задачи;
- определить, как изменятся выручка от реализации продукции и план ее выпуска при увеличении запасов сырья на 18 единиц;
- оценить целесообразность включения в план изделия четвертого вида ценой 70 единиц, на изготовление которого расходуется по две единицы каждого вида ресурсов.
2.6. На основании информации, приведенной в таблице, решается задача оптимального использования ресурсов на максимум выручки от реализации готовой продукции.
| Вид сырья | Нормы расхода сырья на ед., продукции | Запасы сырья | ||
|---|---|---|---|---|
| А | Б | В | ||
| I | 18 | 15 | 12 | 360 |
| II | 6 | 4 | 8 | 192 |
| III | 5 | 3 | 3 | 180 |
| Цена изделия | 9 | 10 | 16 | |
Требуется:
- Сформулировать прямую оптимизационную задачу на максимум выручки от реализации готовой продукции, получить оптимальный план выпуска продукции.
- Сформулировать двойственную задачу и найти ее оптимальный план с помощью теорем двойственности.
- Пояснить нулевые значения переменных в оптимальном плане.
- На основе свойств двойственных оценок и теорем двойственности:
- проанализировать использование ресурсов в оптимальном плане исходной задачи;
- определить, как изменятся выручка от реализации продукции и план ее выпуска, если запас сырья I вида увеличить на 45 кг, а II - уменьшить на 9 кг;
- оценить целесообразность включения в план изделия Г ценой 11 единиц, на изготовление которого расходуется 9, 4 и 6 кг соответствующего вида сырья.
2.7. Предприятие выпускает четыре вида продукции и использует три вида оборудования: токарное, фрезерное, шлифовальное. Общий фонд рабочего времени оборудования каждого вида, нормы расхода и цены реализации единицы каждого вида продукции приведены в таблице.
| Тип оборудования | Нормы расхода ресурса на одно изделие | Фонд рабочего времени, ч | |||
|---|---|---|---|---|---|
| А | Б | В | Г | ||
| Токарное | 2 | 1 | 1 | 3 | 300 |
| Фрезерное | 1 | 0 | 2 | 1 | 70 |
| Шлифовальное | 1 | 2 | 1 | 0 | 340 |
| Цена изделия | 8 | 3 | 2 | 1 | |
Требуется:
- Сформулировать прямую оптимизационную задачу на максимум выручки от реализации готовой продукции, получить оптимальный план выпуска продукции.
- Сформулировать двойственную задачу и найти ее оптимальный план с помощью теорем двойственности.
- Пояснить нулевые значения переменных в оптимальном плане.
- На основе свойств двойственных оценок и теорем двойственности:
- проанализировать использование ресурсов в оптимальном плане исходной задачи;
- определить, как изменятся выручка и план выпуска продукции, если фонд рабочего времени шлифовального оборудования увеличить на 24 часа;
- оценить целесообразность включения в план изделия Д ценой 11 единиц, если нормы затрат оборудования 8, 2 и 2 единицы соответственно.
2.8. На основании информации, приведенной в таблице, решается задача оптимального использования ресурсов на максимум выручки от реализации готовой продукции.
| Тип сырья | Нормы расхода сырья на ед. продукции | Запасы сырья | ||
|---|---|---|---|---|
| I вид | II вид | III вид | ||
| I | 1 | 2 | 1 | 430 |
| II | 3 | 0 | 2 | 460 |
| III | 1 | 4 | 0 | 420 |
| Цена изделия | 3 | 2 | 5 | |
Требуется:
- Сформулировать прямую оптимизационную задачу на максимум выручки от реализации готовой продукции, получить оптимальный план выпуска продукции.
- Сформулировать двойственную задачу и найти ее оптимальный план с помощью теорем двойственности.
- Пояснить нулевые значения переменных в оптимальном плане.
- На основе свойств двойственных оценок и теорем двойственности:
- проанализировать использование ресурсов в оптимальном плане исходной задачи;
- определить, как изменятся выручка от реализации продукции и план ее выпуска, если запас сырья I вида увеличить на 5 единиц, а II - уменьшить на 5 единиц;
- оценить целесообразность включения в план изделия четвертого вида ценой 7 у.е., если нормы затрат сырья 2, 4 и 3 единицы.
2.9. Для изготовления четырех видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и цены реализации единицы каждого вида продукции приведены в таблице.
| Тип сырья | Нормы расхода сырья на одно изделие | Запасы сырья | |||
|---|---|---|---|---|---|
| А | Б | В | Г | ||
| I | 2 | 1 | 0,5 | 4 | 2400 |
| II | 1 | 5 | 3 | 0 | 1200 |
| III | 3 | 0 | 6 | 1 | 3000 |
| Цена изделия | 7,5 | 3 | 6 | 12 | |
Требуется:
- Сформулировать прямую оптимизационную задачу на максимум выручки от реализации готовой, продукции, получить оптимальный план выпуска продукции.
- Сформулировать двойственную задачу и найти ее оптимальный план с помощью теорем двойственности. ч
- Пояснить нулевые значения переменных в оптимальном плане.
- На основе свойств двойственных оценок и теорем двойственности:
- проанализировать использование ресурсов в оптимальном плане исходной задачи;
- определить, как изменятся выручка и план выпуска продукции при увеличении запасов сырья I вида на 100 единиц и уменьшении на 150 единиц запасов сырья II вида;
- оценить целесообразность включения в план изделия Д ценой 10 единиц, если нормы затрат сырья 2, 4 и 3 единицы.
2.10. Для изготовления трех видов продукции используют четыре вида ресурсов. Запасы ресурсов, нормы расхода и цены реализации единицы каждого вида продукции приведены в таблице.
| Вид ресурсов | Нормы расхода ресурсов на ед. продукции | Запасы ресурсов | ||
|---|---|---|---|---|
| I вид | II вид | III вид | ||
| Труд | 3 | 6 | 4 | 2000 |
| Сырье 1 | 20 | 15 | 20 | 15000 |
| Сырье 2 | 10 | 15 | 20 | 7400 |
| Оборудование | 0 | 3 | 5 | 1500 |
| Цена изделия | 6 | 10 | 9 | |
Требуется:
- Сформулировать прямую оптимизационную задачу на максимум выручки от реализации готовой продукции, получить оптимальный план выпуска продукции.
- Сформулировать двойственную задачу и найти ее оптимальный план с помощью теорем двойственности.
- Пояснить нулевые значения переменных в оптимальном плане.
- На основе свойств двойственных оценок и теорем двойственности:
- проанализировать использование ресурсов в оптимальном плане исходной задачи;
- определить, как изменятся выручка и план выпуска продукции при увеличении запаса ресурса первого вида на 24 единицы;
- оценить целесообразность включения в план изделия четвертого вида ценой 11 единиц, если нормы затрат ресурсов 8, 4, 20 и 6 единиц.
Задача 3
Используя балансовый метод планирования и модель Леонтьева, построить баланс производства и распределения продукции предприятий2.
Задачи 3.1-3.10. Промышленная группа предприятий (холдинг) выпускает продукцию трех видов, при этом каждое из трех предприятий группы специализируется на выпуске продукции одного вида: первое предприятие специализируется на выпуске продукции первого вида, второе предприятие - продукции второго вида; третье предприятие - продукции третьего вида. Часть выпускаемой продукции потребляется предприятиями холдинга (идет на внутреннее потребление), остальная часть поставляется за его пределы (внешним потребителям, является конечным продуктом). Специалистами управляющей компании получены экономические оценки аij (i = 1, 2, 3; j = 1, 2, 3) элементов технологической матрицы А (норм расхода, коэффициентов прямых материальных затрат) и элементов уi. вектора конечной продукции Y.
Требуется:
- Проверить продуктивность технологической матрицы А = (аij) (матрицы коэффициентов прямых материальных затрат).
- Построить баланс (заполнить таблицу) производства и распределения продукции предприятий холдинга.
В соответствии с номером вашего варианта ниже в табл. 1 выберите числовые значения для табл. 2.
Таблица 1
| Вариант № | Для первой строки | Для второй строки | Для третьей строки | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1А | 2А | 3А | 4А | 1Б | 2Б | 3Б | 4Б | 1В | 2В | 3В | 4В | |
| 1 | 0,1 | 0,2 | 0,1 | 200 | 0,2 | 0,1 | 0,0 | 150 | 0,0 | 0,2 | 0,1 | 250 |
| 2 | 0,0 | 0,1 | 0,2 | 180 | 0,1 | 0,2 | 0,1 | 200 | 0,2 | 0,1 | 0,2 | 200 |
| 3 | 0,2 | 0,1 | 0,2 | 150 | 0,0 | 0,1 | 0,2 | 180 | 0,1 | 0,0 | 0,1 | 100 |
| 4 | 0,1 | 0,0 | 0,1 | 100 | 0,1 | 0,0 | 0,2 | 300 | 0,2 | 0,1 | 0,0 | 160 |
| 5 | 0,2 | 0,3 | 0,0 | 120 | 0,3 | 0,1 | 0,2 | 250 | 0,1 | 0,0 | 0,3 | 180 |
| 6 | 0,3 | 0,4 | 0,1 | 200 | 0,1 | 0,2 | 0,4 | 300 | 0,3 | 0,4 | 0,1 | 200 |
| 7 | 0,1 | 0,2 | 0,4 | 100 | 0,0 | 0,4 | 0,1 | 200 | 0,1 | 0,3 | 0,4 | 100 |
| 8 | 0,0 | 0,4 | 0,1 | 160 | 0,4 | 0,1 | 0,0 | 180 | 0,3 | 0,0 | 0,1 | 150 |
| 9 | 0,4 | 0,2 | 0,3 | 180 | 0,2 | 0,1 | 0,0 | 200 | 0,2 | 0,1 | 0,0 | 160 |
| 10 | 0,1 | 0,1 | 0,2 | 160 | 0,1 | 0,2 | 0,3 | 180 | 0,1 | 0,2 | 0,3 | 170 |
Таблица 2
| Предприятия (виды продукции) | Коэффициенты прямых затрат aij | Конечный продукт Y | ||
|---|---|---|---|---|
| 1 | 2 | 3 | ||
| 1 | 1А | 2А | 3А | 4А |
| 2 | 1Б | 2Б | 3Б | 4Б |
| 3 | 1B | 2В | 3В | 4В |
Задача 4
Исследовать динамику экономического показателя на основе анализа одномерного временного ряда3
Задачи 4.1-4.10. В течение девяти последовательных недель фиксировался спрос Y(t) (млн руб.) на кредитные ресурсы финансовой компании. Временной ряд Y(t) этого показателя (повариантно) приведен ниже в таблице.
| Номер варианта | Номер наблюдения (t = 1, 2, ..., 9) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 10 | 14 | 21 | 24 | 33 | 41 | 44 | 47 | 49 |
| 2 | 43 | 47 | 50 | 48 | 54 | 57 | 61 | 59 | 65 |
| 3 | 3 | 7 | 10 | 11 | 15 | 17 | 21 | 25 | 23 |
| 4 | 30 | 28 | 33 | 37 | 40 | 42 | 44 | 49 | 47 |
| 5 | 5 | 7 | 10 | 12 | 15 | 18 | 20 | 23 | 26 |
| 6 | 12 | 15 | 16 | 19 | 17 | 20 | 24 | 25 | 28 |
| 7 | 20 | 27 | 30 | 41 | 45 | 51 | 51 | 55 | 61 |
| 8 | 8 | 13 | 15 | 19 | 25 | 27 | 33 | 35 | 40 |
| 9 | 45 | 43 | 40 | 36 | 38 | 34 | 31 | 28 | 25 |
| 10 | 33 | 35 | 40 | 41 | 45 | 47 | 45 | 51 | 53 |
Требуется:
- Проверить наличие аномальных наблюдений.
- Построить линейную модель
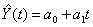 , параметры
которой оценить МНК (
, параметры
которой оценить МНК (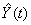 - расчетные, смоделированные
значения временного ряда).
- расчетные, смоделированные
значения временного ряда). - Построить адаптивную модель Брауна4 с параметром сглаживания α = 0,4 и α = 0,7; выбрать лучшее значение параметра сглаживания.
- Оценить адекватность построенных моделей, используя свойства независимости остаточной компоненты, случайности и соответствия нормальному закону распределения (при использовании R/S-критерия взять табулированные границы 2,7-3,7).
- Оценить точность моделей на основе использования средней относительной ошибки аппроксимации.
- По двум построенным моделям осуществить прогноз спроса на следующие две недели (доверительный интервал прогноза рассчитать при доверительной вероятности р = 70%).
- Фактические значения показателя, результаты моделирования и прогнозирования представить графически.
Вычисления провести с одним знаком в дробной части. Основные промежуточные результаты вычислений представить в таблицах (при использовании компьютера представить соответствующие листинги с комментариями).
1 Нахождение оптимального плана задачи может быть получено с помощью надстройки Excel Поиск решения или «вручную» симплексным методом.
2 Студенты специальности 060400 не решают данную задачу.
3 При решении данной задачи расчеты можно вести с использованием надстройки Excel Анализ данных.
4 Пункт 3 выполняют только студенты специальности 060400.