Тема 1. Введение. Эконометрика и эконометрическое моделирование
Тема 3. Парная регрессия и корреляция
Тема 4. Модель множественной регрессии
Тема 5. Системы линейных одновременных уравнений
Тема 6. Многомерный статистический анализ
Задания для выполнения контрольной работы по дисциплине
Тема 3. Парная регрессия и корреляция
Экономические данные представляют собой количественные характеристики каких-либо экономических объектов или процессов. Они формируются под действием множества факторов, не все из которых доступны внешнему контролю. Неконтролируемые факторы могут принимать случайные значения из некоторого множества значений и тем самым обусловливать случайность данных, которые они определяют. Стохастическая (вероятностная) природа экономических данных обусловливает необходимость применения соответствующих статистических методов для их обработки и анализа.
Статистические распределения характеризуются наличием более или менее значительной вариации в величине признака у отдельных единиц совокупности. Естественно, возникает вопрос о том, какие же причины формируют уровень признака в данной совокупности и каков конкретный вклад каждой из них. Изучение зависимости вариации признака от окружающих условий и составляет содержание теории корреляции1.
Изучение действительности показывает, что вариация каждого изучаемого признака находится в тесной связи и взаимодействии с вариацией других признаков, характеризующих исследуемую совокупность единиц. Вариация уровня производительности труда работников предприятий зависит от степени совершенства применяемого оборудования, технологии, организации производства, труда и управления и других самых различных факторов.
При изучении конкретных зависимостей одни признаки выступают в качестве факторов, обусловливающих изменение других признаков. Признаки этой первой группы в дальнейшем будем называть признаками-факторами (факторными признаками); а признаки, которые являются результатом влияния этих факторов, будем называть результативными. Например, при изучении зависимости между производительностью труда рабочих и энерговооруженностью их труда уровень производительности труда является результативным признаком, а энерговооруженность труда рабочих — факторным признаком.
Рассматривая зависимости между признаками, необходимо выделить, прежде всего две категории зависимости: 1) функциональные и 2) корреляционные.
Функциональные связи характеризуются полным соответствием между изменением факторного признака и изменением результативной величины, и каждому значению признака-фактора соответствуют вполне определенные значения результативного признака. Функциональная зависимость может связывать результативный признак с одним или несколькими факторными признаками. Так, величина начисленной заработной платы при повременной оплате труда зависит от количества отработанных часов.
В корреляционных связях между изменением факторного и результативного признака нет полного соответствия, воздействие отдельных факторов проявляется лишь в среднем при массовом наблюдении фактических данных. Одновременное воздействие на изучаемый признак большого количества самых разнообразных факторов приводит к тому, что одному и тому же значению признака-фактора соответствует целое распределение значений результативного признака, поскольку в каждом конкретном случае прочие факторные признаки могут изменять силу и направленность своего воздействия.
При сравнении функциональных и корреляционных зависимостей следует иметь в виду, что при наличии функциональной зависимости между признаками можно, зная величину факторного признака, точно определить величину результативного признака. При наличии же корреляционной зависимости устанавливается лишь тенденция изменения результативного признака при изменении величины факторного признака. В отличие от жесткости функциональной связи корреляционные связи характеризуются множеством причин и следствий и устанавливаются лишь их тенденции.
3.1. Корреляционный анализ
Основная задача корреляционного анализа заключается в выявлении взаимосвязи между случайными переменными путем точечной и интервальной оценки парных (частных) коэффициентов корреляции, вычисления и проверки значимости множественных коэффициентов корреляции и детерминации. Кроме того, с помощью корреляционного анализа решаются следующие задачи: отбор факторов, оказывающих наиболее существенное влияние на результативный признак, на основании измерения степени связи между ними; обнаружение ранее неизвестных причинных связей. Корреляция непосредственно не выявляет причинных связей между параметрами, но устанавливает численное значение этих связей и достоверность суждений об их наличии.
Выборочная ковариация является мерой взаимосвязи между двумя переменными.
Ковариация между двумя переменными x и y рассчитывается следующим образом:
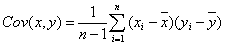
где (x1, y1), (x2,
y2), …, (xn, yn)
– фактические значения случайных переменных X и Y,
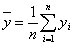 ;
; 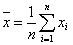 .
.
Ковариация - это статистическая мера взаимодействия двух случайных переменных, таких, например, как доходности двух ценных бумаг. Положительное значение ковариации показывает, что доходности этих ценных бумаг имеют тенденцию изменяться в одну сторону.
Ковариация зависит от единиц, в которых измеряются переменные X и Y.
Поэтому для измерения силы связи между двумя переменными используется другая статистическая характеристика, называемая коэффициентом корреляции.
При проведении корреляционного анализа вся совокупность данных рассматривается как множество переменных (факторов), каждая из которых содержит n - наблюдений; xik — i-e наблюдение k-й переменной. Основными средствами анализа данных являются парные коэффициенты корреляции, частные коэффициенты корреляции и множественные коэффициенты корреляции.
Коэффициент парной корреляции
Для двух переменных X и Y теоретический коэффициент корреляции определяется следующим образом:
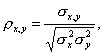
где 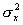 ,
,
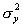 — дисперсии случайных переменных X
и Y, а σx, y – их ковариация.
— дисперсии случайных переменных X
и Y, а σx, y – их ковариация.
Парный коэффициент корреляции является показателем тесноты связи лишь в случае линейной зависимости между переменными и обладает следующими основными свойствами:
Коэффициент корреляции принимает значение и интервале (-1, +1), или |ρxy| < 1;
Коэффициент корреляции не зависит от выбора начала отсчета и единицы измерения, т.е.
ρ(α1X + β; α2Y + β) = ρxy
где α1, α2, β - постоянные величины, причем α1 > 0, α2 > 0.
Случайные величины X, Y можно уменьшать (увеличивать) в α раз, а также вычитать или прибавлять к значениям X и Y одно и тоже число β - это не приведет к изменению коэффициента корреляции ρ.
При ρ = ±1 корреляционная связь представляется линейной функциональной зависимостью, т.е. Y = αX + β.
При ρ = 0 линейная корреляционная связь отсутствует.
В практических расчетах коэффициент корреляции ρ генеральной совокупности обычно не известен. По результатам выборки может быть найдена его точечная оценка — выборочный коэффициент корреляции r, так как выборочная совокупность переменных X и Y случайна, то в отличие от параметра ρ, r - случайная величина. Оценкой коэффициента корреляции ρ является выборочный парный коэффициент корреляции:
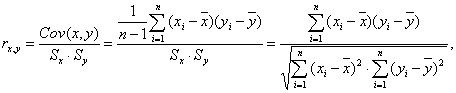 (3.1)
(3.1)
где 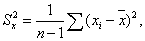
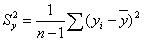 - оценки дисперсий X и Y.
- оценки дисперсий X и Y.
Для оценки значимости коэффициента корреляции применяется t-критерий Стьюдента. При этом фактическое значение этого критерия определяется по формуле:
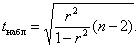 (3.2)
(3.2)
Вычисленное по этой формуле значение tнабл сравнивается с критическим значением t-критерия, которое берется из таблицы значений t Стьюдента с учетом заданного уровня значимости и числа степеней свободы.
Если tнабл > tкр, то полученное значение коэффициента корреляции признается значимым (то есть нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается). И таким образом делается вывод о том, что между исследуемыми переменными есть тесная статистическая взаимосвязь.
Если значение ry,x близко к нулю, связь между переменными слабая. Если случайные величины связаны положительной корреляцией, это означает, что при возрастании одной случайной величины другая имеет тенденцию в среднем возрастать. Если случайные величины связаны отрицательной корреляцией, это означает, что при возрастании одной случайной величины другая имеет тенденцию в среднем убывать.
Коэффициенты парной корреляции используются для измерения силы линейных связей различных пар признаков из их множества. Для множества m признаков n наблюдений получают матрицу коэффициентов парной корреляции R.
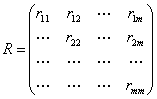 (3.3)
(3.3)
Одной корреляционной матрицей нельзя полностью описать зависимости между величинами. В связи с этим в многомерном корреляционном анализе рассматривается две задачи:
1) определение тесноты связи одной случайной величины с совокупностью остальных (m-1) величин, включенных в анализ;
2) определение тесноты связи между величинами при фиксировании или исключении влияния остальных k величин, при k < (m-2).
Эти задачи решаются с помощью коэффициентов множественной и частной корреляции соответственно.
Множественный коэффициент корреляции
Решение первой задачи осуществляется с помощью выборочного коэффициента множественной корреляции по формуле:
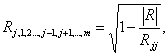 (3.4)
(3.4)
где |R| - определитель корреляционной матрицы R (3.3);
Rjj - алгебраическое дополнение элемента rjj той же матрицы R.
Квадрат коэффициента множественной корреляции
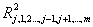 принято называть выборочным множественным
коэффициентом детерминации, который показывает, какую долю вариации
(случайного разброса) исследуемой величины Xj объясняет
вариация остальных случайных величин X1, X2,
..., Xm.
принято называть выборочным множественным
коэффициентом детерминации, который показывает, какую долю вариации
(случайного разброса) исследуемой величины Xj объясняет
вариация остальных случайных величин X1, X2,
..., Xm.
Коэффициенты множественной корреляции и детерминации являются величинами положительными, принимающими значения в интервале от 0 до 1. При приближении коэффициента R2 к единице можно сделать вывод о тесноте взаимосвязи случайных величин, но не о ее направлении. Коэффициент множественной корреляции может только увеличиваться, если в модель включать дополнительные переменные, и не увеличится, если из имеющихся признаков производить исключение.
Проверка значимости коэффициента множественной корреляции осуществляется путем сравнения расчетного значения критерия Фишера
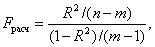 (3.5)
(3.5)
с табличным Fтабл Табличное значение критерия определяется заданным уровнем значимости а и степенями свободы k1 = m-1 и k2 = n-m. Коэффициент R2 значимо отличается от нуля, если выполняется неравенство
Fрасч > Fтабл.
Частный коэффициент корреляции
Если рассматриваемые случайные величины коррелируют друг с другом, то на величине коэффициента парной корреляции частично сказывается влияние других величин. В связи с этим возникает необходимость исследования частной корреляции между величинами при исключении влияния одной или нескольких других случайных величин.
Выборочный частный коэффициент корреляции определяется по формуле:
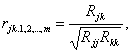
где Rjk, Rjj, Rkk — алгебраические дополнения к соответствующим элементам матрицы (3.3).
Частный коэффициент корреляции, так же, как и парный коэффициент корреляции изменяется от -1 до +1.
Пример 3.1. Вычисление коэффициентов парной, множественной и частной корреляции
В табл. 3.1 представлены информация об объемах продаж и затратах на рекламу одной фирмы, а также индекс потребительских расходов за ряд текущих лет.
Требуется:
1. Построить диаграмму рассеяния (корреляционное поле) для переменных «объемы продаж» и «индекс потребительских расходов».
2. Определить степень влияния индекса потребительских расходов на объемы продаж (вычислить коэффициент парной корреляции).
3. Оценить значимость вычисленного коэффициента парной корреляции.
4. Построить матрицу коэффициентов парной корреляции по трем переменным.
5. Найти оценку множественного коэффициента корреляции.
6. Найти оценки коэффициентов частной корреляции.
Таблица 3.1
| Объем продаж, Y, тыс. руб. | 126 | 137 | 148 | 191 | 274 | 370 | 432 | 445 |
| Затраты на рекламу, X1 | 4 | 4,8 | 3,8 | 8,7 | 8,2 | 9,7 | 14,7 | 18,7 |
| Индекс потребительских расходов, X2, % | 100 | 98,4 | 101,2 | 103,5 | 104,1 | 107 | 107,4 | 108,5 |
Продолжение табл. 3.1
| Объем продаж, Y, тыс. руб. | 367 | 367 | 321 | 307 | 331 | 345 | 364 | 384 |
| Затраты на рекламу, X1 | 19,8 | 10,6 | 8,6 | 6,5 | 12,6 | 6,5 | 5,8 | 5,7 |
| Индекс потребительских расходов, X2, % | 108,3 | 109,2 | 110,1 | 110,7 | 110,3 | 111,8 | 112,3 | 112,9 |
Решение
1. Вытянутость облака точек на диаграмме рассеяния вдоль наклонной прямой позволяет сделать предположение, что существует некоторая объективная тенденция прямой линейной связи между значениями переменных X — индекс потребительских расходов и Y — объемы продаж.
В нашем примере диаграмма рассеяния имеет вид, приведенный на рис 3.1.
2. Промежуточные расчеты при вычислении коэффициента корреляции между переменными X — индекс потребительских расходов и Y — объемы продаж приведены в табл. 3.2.
Средние значения случайных величин X и Y, которые являются наиболее простыми показателями, характеризующими последовательности x1, x2, …, x16 и y1, y2, …, y16, рассчитаем по формулам, соответственно
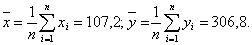
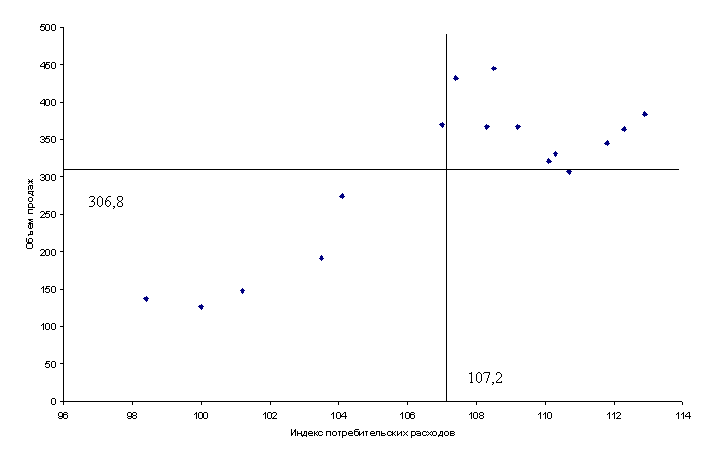
Рис. 3.1. Диаграмма рассеяния (корреляционное поле)
Дисперсия характеризует степень разброса значений x1,
x2, …, x16 (y1,
y2, …, y16) вокруг своего среднего
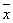 (и соответственно
(и соответственно
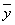 ):
):

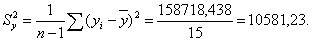
Стандартные ошибки случайных величин X и Y рассчитаем по формулам соответственно:
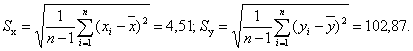
Коэффициент корреляции рассчитаем по формуле (3.1):
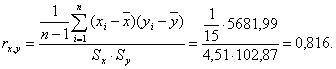
Таблица 3.2
| № | Y | X | 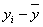 |
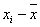 |
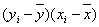 |
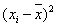 |
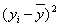 |
|---|---|---|---|---|---|---|---|
| 1 | 126 | 100 | -180,813 | -7,231 | 1307,500 | 52,291 | 32693,160 |
| 2 | 137 | 98,4 | -169,813 | -8,831 | 1499,657 | 77,991 | 28836,285 |
| 3 | 148 | 101,2 | -158,813 | -6,031 | 957,838 | 36,376 | 25221,410 |
| 4 | 191 | 103,5 | -115,813 | -3,731 | 432,125 | 13,922 | 13412,535 |
| 5 | 274 | 104,1 | -32,813 | -3,131 | 102,744 | 9,805 | 1076,660 |
| 6 | 370 | 107 | 63,188 | -0,231 | -14,612 | 0,053 | 3992,660 |
| 7 | 432 | 107,4 | 125,188 | 0,169 | 21,125 | 0,028 | 15671,910 |
| 8 | 445 | 108,5 | 138,188 | 1,269 | 175,325 | 1,610 | 19095,785 |
| 9 | 367 | 108,3 | 60,188 | 1,069 | 64,325 | 1,142 | 3622,535 |
| 10 | 367 | 109,2 | 60,188 | 1,969 | 118,494 | 3,876 | 3622,535 |
| 11 | 321 | 110,1 | 14,188 | 2,869 | 40,700 | 8,230 | 201,285 |
| 12 | 307 | 110,7 | 0,188 | 3,469 | 0,650 | 12,032 | 0,035 |
| 13 | 331 | 110,3 | 24,188 | 3,069 | 74,225 | 9,417 | 585,035 |
| 14 | 345 | 111,8 | 38,188 | 4,569 | 174,469 | 20,873 | 1458,285 |
| 15 | 364 | 112,3 | 57,188 | 5,069 | 289,869 | 25,692 | 3270,410 |
| 16 | 384 | 112,9 | 77,188 | 5,669 | 437,557 | 32,135 | 5957,910 |
| Сумма | 4909 | 1715,7 | 0,000 | 0,000 | 5681,994 | 305,474 | 158718,438 |
| Среднее | 306,8125 | 107,23125 |
3. Оценим значимость коэффициента корреляции. Для этого рассчитаем значение t-статистики по формуле
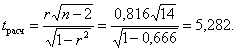
Табличное значение критерия Стьюдента равно: tтабл (α = 0,1; k = n - 2 = 14) = 1,76 (см. Приложение 2). Сравнивая числовые значения критериев, видно, что tрасч > tтабл, т.е. полученное значение коэффициента корреляции значимо.
Таким образом, индекс потребительских расходов оказывает весьма высокое влияние на объемы продаж.
4. Матрица R коэффициентов парной корреляции, вычисленных по формуле (3.1), для трех факторов будет иметь вид:
| Объем реализации 1 | Затраты на рекламу 2 | Индекс потребительских расходов 3 | |
| Объем реализации 1 | 1 | 0,646 | 0,816 |
| Затраты на рекламу 2 | 0,646 | 1 | 0,273 |
| Индекс потребительских расходов 3 | 0,816 | 0,273 | 1 |
5. Вычисление множественного коэффициента корреляции y с x1 и x2:
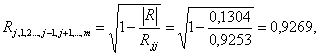
где |R| — определитель корреляционной матрицы R равен 0,1304,
R11 — алгебраическое дополнение 1-го диагонального элемента той же матрицы R:
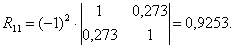
6. Вычисление коэффициентов частной корреляции:
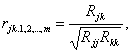
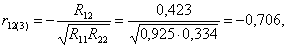
где R12 — алгебраическое дополнение элемента r12 матрицы R, а R22 — алгебраическое дополнение 2-го диагонального элемента r22:
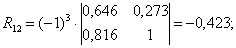
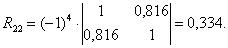
Коэффициенты частной корреляции можно вычислить, используя коэффициенты парной корреляции:
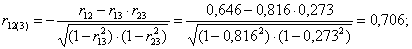
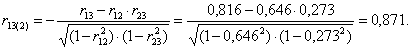
3.2. Регрессионный анализ
Регрессионный анализ предназначен для исследования зависимости исследуемой переменной от различных факторов и отображения их взаимосвязи в форме регрессионной модели.
В регрессионных моделях зависимая (объясняемая) переменная Y может быть представлена в виде функции f(X1, X2, Х3, ..., Xm), где X1, X2, Х3, ..., Xm — независимые (объясняющие) переменные, или факторы. В качестве зависимой переменной может выступать практически любой показатель, характеризующий, например, деятельность предприятия или курс ценной бумаги. В зависимости от вида функции f(X1, X2, Х3, ..., Xm) модели делятся на линейные и нелинейные. В зависимости от количества включенных в модель факторов X модели делятся на однофакторные (парная модель регрессии) и многофакторные (модель множественной регрессии).
Связь между переменной Y и m независимыми факторами можно охарактеризовать функцией регрессии Y = f(X1, X2, Х3, ..., Xm), которая показывает, каково будет в среднем значение переменной yi, если переменные хi примут конкретное значение.
Данное обстоятельство позволяет использовать модель регрессии не только для анализа, но и для прогнозирования экономических явлений. В качестве зависимой переменной может выступать практически любой показатель, характеризующий, например, деятельность коммерческого банка или означающий курс ценной бумаги.
Линейная парная регрессия
Под линейностью здесь имеется в виду, что переменная у предположительно находится под влиянием переменной х в следующей зависимости:
yi = α + β × xi + εi (3.6)
где α — постоянная величина (или свободный член уравнения),
β — коэффициент регрессии, определяющий наклон линии, вдоль которой рассеяны данные наблюдений. Это показатель, характеризующий изменение переменной yi при изменении значения хi на единицу. Если β > 0 — переменные хi и yi положительно коррелированные, если β < 0 — отрицательно коррелированны;
εi — независимая нормально распределенная случайная величина — остаток с нулевым математическим ожиданием (mε = 0) и постоянной дисперсией (Dε = σ2). Она отражает тот факт, что изменение yi будет неточно описываться изменением X: присутствуют другие факторы, не учтенные в данной модели.
Оценка параметров регрессионного уравнения
Основные предпосылки метода наименьших квадратов
Свойства коэффициентов регрессии существенным образом зависят от свойств случайной составляющей. Для того чтобы регрессионный анализ, основанный на обычном методе наименьших квадратов, давал наилучшие из всех возможных результаты, должны выполняться следующие условия, известные как условия Гаусса-Маркова.
- Первое условие. Математическое ожидание случайной составляющей в любом наблюдении должно быть равно нулю. Иногда случайная составляющая будет положительной, иногда — отрицательной, но она не должна иметь систематического смещения ни в одном из двух возможных направлений.
M(εi) = 0.
Фактически, если уравнение регрессии включает постоянный член, то обычно это условие выполняется автоматически, так как роль константы состоит в определении любой систематической тенденции Y, которую не учитывают объясняющие переменные, включенные в уравнение регрессии.
- Второе условие состоит в том, что в модели (3.6) возмущение εi (или зависимая переменная yi) есть величина случайная, а объясняющая переменная xi — величина неслучайная.
Если это условие выполнено, то теоретическая ковариация между независимой переменной и случайным членом равна нулю.
- Третье условие предполагает отсутствие систематической связи между значениями случайной составляющей в любых двух наблюдениях. Например, если случайная составляющая велика и положительна в одном наблюдении, это не должно обусловливать систематическую тенденцию к тому, что она будет большой и положительной в следующем наблюдении. Случайные составляющие должны быть независимы друг от друга.
В силу того, что M(εi) = M(εj) = 0, данное условие можно записать следующим образом:
M(εi, εj) = 0 (i ≠ j).
Возмущения εi и εj не коррелированны (условие независимости случайных составляющих в различных наблюдениях).
Это условие означает, что отклонения регрессии (а значит, и сама зависимая переменная) не коррелируют. Условие некоррелируемости ограничительно, например, в случае временного ряда yt.Тогда третье условие означает отсутствие автокорреляции ряда εt.
- Четвертое условие означает, что дисперсия случайной доставляющей
должна быть постоянна для всех наблюдений. Иногда случайная составляющая
будет больше, иногда — меньше, однако не должно быть априорной причины
для того, чтобы она порождала большую ошибку в одних наблюдениях, чем
в других. Эта постоянная дисперсия обычно обозначается σ2(ε),
или часто в более краткой форме
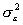 ,
а условие записывается следующим образом:
,
а условие записывается следующим образом:
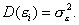
Величина σ2(ε), конечно, неизвестна. Одна из задач регрессионного анализа состоит в оценке стандартного отклонения случайной составляющей. Это условие гомоскедастичности, или равноизменчивости случайной составляющей (возмущения).
- Предположение о нормальности. Наряду с условиями Гаусса-Маркова обычно также предполагается нормальность распределения случайного члена. Дело в том, что если случайный член нормально распределен, то так же будут распределены и коэффициенты регрессии.
Свойства оценок МНК
В тех случаях, когда предпосылки выполняются, оценки, полученные по МНК, будут обладать свойствами несмещенности, состоятельности и эффективности.
Несмещенность оценки означает, что математическое ожидание остатков равно нулю. Если оценки обладают свойством несмещенности, то их можно сравнивать по разным исследованиям.
Для практических целей важна не только несмещенность, но и эффективность оценок.
Оценки считаются эффективными, если они характеризуются наименьшей дисперсией. Поэтому несмещенность оценки должна дополняться минимальной дисперсией.
Степень реалистичности доверительных интервалов параметров регрессии обеспечивается, если оценки будут не только несмещенными и эффективными, но и состоятельными.
Состоятельность оценок характеризует увеличение их точности с увеличением объема выборки.
Для оценки параметров регрессионного уравнения наиболее часто
используют метод наименьших квадратов (МНК), который минимизирует сумму
квадратов отклонения наблюдаемых значений yi, от
модельных значений 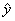 .
.
Согласно принципу метода наименьших квадратов оценки
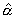 и
и 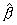 находятся путем минимизации суммы квадратов:
находятся путем минимизации суммы квадратов:
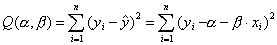
по всем возможным значениям α и β при заданных (наблюдаемых) значениях х1, ..., хn, y1, ..., yn. Задача сводится к известной математической задаче поиска точки минимума функции двух переменных. Такая точка находится путем приравнивания нулю частных производных функции z = Q(α, β) по переменным α и β. Это приводит к системе нормальных уравнений:
∂Q(α, β)/∂α = 0, ∂Q(α, β)/∂β = 0,
решением которой и является пара
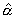 ,
, 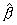 .
Следует заметить, что согласно правилам вычисления производных,
.
Следует заметить, что согласно правилам вычисления производных,
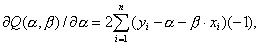
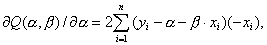
так что искомые значения 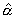 ,
,
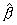 удовлетворяют соотношениям
удовлетворяют соотношениям
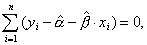
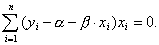
Эту систему двух уравнений можно записать также в виде
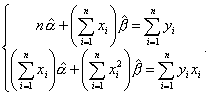
Эта система является системой двух линейных уравнений с двумя неизвестными и может быть легко решена, например методом подстановки. В результате получаем:
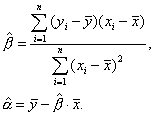 (3.7)
(3.7)
Такое решение может существовать только при выполнении условия
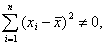
что равносильно отличию от нуля определителя системы нормальных уравнений. Действительно, этот определитель равен:
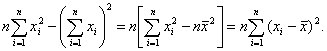
Последнее условие называется условием идентифицируемости
модели наблюдений yi = (α + β × xi)
+ εi, i = 1, ..., n и означает, что не все
значения х1, ..., хn, совпадают
между собой. При нарушении этого условия все точки (хi,
уi), i = 1, ..., n, лежат на одной
вертикальной прямой 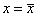 .
.
Оценки 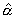 и
и
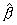 называют: оценками наименьших квадратов.
Обратим еще раз внимание на полученное выражение для
называют: оценками наименьших квадратов.
Обратим еще раз внимание на полученное выражение для
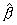 . Нетрудно увидеть, что в это выражение
входят уже знакомые нам суммы квадратов, участвовавшие ранее в определении
выборочной дисперсии
. Нетрудно увидеть, что в это выражение
входят уже знакомые нам суммы квадратов, участвовавшие ранее в определении
выборочной дисперсии 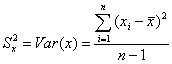 и выборочной ковариации
и выборочной ковариации
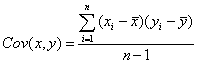 , так что в этих терминах
, так что в этих терминах
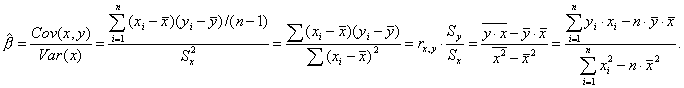 (3.8)
(3.8)
Матричная форма записи
В матричной форме модель парной регрессии имеет вид
Y = X - A + ε, (3.9)
где Y — вектор-столбец размерности (n × 1) наблюдаемых значений зависимой переменной;
X — матрица размерности (n × 2) наблюдаемых значений факторных признаков. Дополнительный фактор x0 вводится для вычисления свободного члена;
A — вектор-столбец размерности (2 × 1) неизвестных, подлежащих оценке коэффициентов регрессии;
ε — вектор-столбец размерности (n × 1) ошибок наблюдений
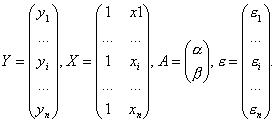
Решение системы нормальных уравнений в матричной форме имеет вид
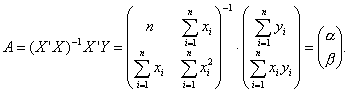
Пример 3.2
Бюджетное обследование семи случайно выбранных семей дало следующие результаты (в тыс. долл.):
Таблица 3.2
| Наблюдение | Накопления, Y | Доход, X |
|---|---|---|
| 1 | 3 | 40 |
| 2 | 6 | 55 |
| 3 | 5 | 45 |
| 4 | 3,5 | 30 |
| 5 | 1,5 | 30 |
| 6 | 4,5 | 50 |
| 7 | 2 | 35 |
Требуется:
1. Построить однофакторную модель регрессии,
2. Отобразить на графике исходные данные, результаты моделирования.
Решение
Для вычисления параметров модели следует воспользоваться формулами (3.7) и (3.8). Промежуточные расчеты приведены в таблице 3.3.
Таблица 3.3
| Наблюдение | Накопления, Y | Доход, X | 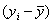 |
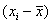 |
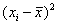 |
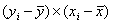 |
yx | X2 |
|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 40 | -0,643 | -0,714 | 0,510 | 0,459 | 120 | 1600 |
| 2 | 6 | 55 | 2,357 | 14,286 | 204,082 | 33,673 | 330 | 3025 |
| 3 | 5 | 45 | 1,357 | 4,286 | 18,367 | 5,816 | 225 | 2025 |
| 4 | 3,5 | 30 | -0,143 | -10,714 | 114,796 | 1,531 | 105 | 900 |
| 5 | 1,5 | 30 | -2,143 | -10,714 | 114,796 | 22,959 | 45 | 900 |
| 6 | 4,5 | 50 | 0,857 | 9,286 | 86,224 | 7,959 | 225 | 2500 |
| 7 | 2 | 35 | -1,643 | -5,714 | 32,653 | 9,388 | 70 | 1225 |
| Сумма | 25,5 | 285,00 | 0,000 | 0,000 | 571,429 | 81,786 | 1120 | 12175 |
| Среднее | 3,643 | 40,714 | 160 | 1739,286 |
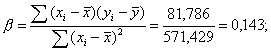
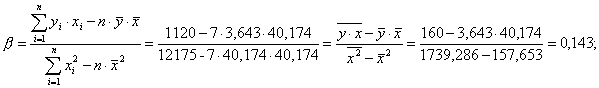
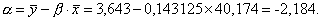
Построена модель зависимости накопления от дохода:
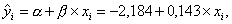
график которой изображен на рис. 3.2.
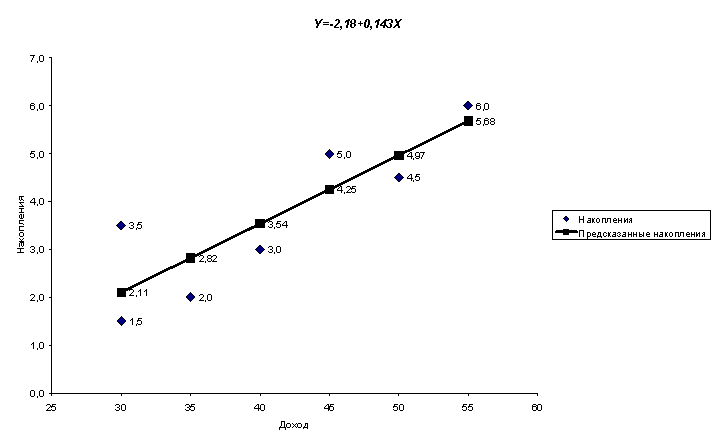
Рис. 3.2. График модели парной регрессии
Качество модели регрессии
Качество модели регрессии связывают с адекватностью модели наблюдаемым (эмпирическим) данным. Проверка адекватности (или соответствия) модели регрессии наблюдаемым данным проводится на основе анализа остатков — εi.
После построения уравнения регрессии мы можем разбить значение
y d каждом наблюдении на две составляющие —
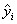 и εi:
и εi:
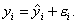 (3.10)
(3.10)
Остаток представляет собой отклонение фактического значения
зависимой переменной от значения данной переменной, полученное расчетным
путем: 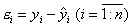 . Если
. Если
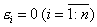 , то для всех наблюдений фактические значения
зависимой переменной совпадают с расчетными (теоретическими) значениями.
Графически это означает, что теоретическая линия регрессии (линия, построенная
по функции
, то для всех наблюдений фактические значения
зависимой переменной совпадают с расчетными (теоретическими) значениями.
Графически это означает, что теоретическая линия регрессии (линия, построенная
по функции 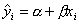 ) проходит через все точки
корреляционного поля, что возможно только при строго функциональной связи.
Следовательно, результативный признак y полностью обусловлен влиянием
фактора x.
) проходит через все точки
корреляционного поля, что возможно только при строго функциональной связи.
Следовательно, результативный признак y полностью обусловлен влиянием
фактора x.
На практике, как правило, имеет место некоторое рассеивание точек корреляционного поля относительно теоретической линии регрессии, т.е. отклонения эмпирических данных от теоретических (εi ≠ 0). Величина этих отклонений и лежит в основе расчета показателей качества (адекватности) уравнения.
При анализе качества модели регрессии используется основное
положение дисперсионного анализа [6], согласно которому общая сумма квадратов
отклонений зависимой переменной от среднего значения
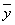 может быть разложена на две составляющие
— объясненную и необъясненную уравнением регрессии дисперсии:
может быть разложена на две составляющие
— объясненную и необъясненную уравнением регрессии дисперсии:
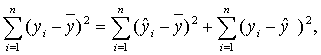 (3.11)
(3.11)
где 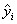 — значения y,
вычисленные по модели
— значения y,
вычисленные по модели 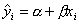 .
.
Разделив правую и левую часть (3.11) на
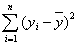
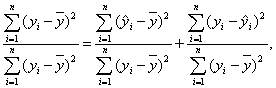
получим
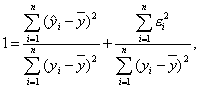
Коэффициент детерминации определяется следующим образом:
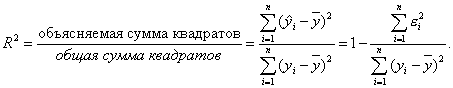 (3.12)
(3.12)
Коэффициент детерминации показывает долю вариации результативного признака, находящегося под воздействием изучаемых факторов, т.е. определяет, какая доля вариации признака Y учтена в модели и обусловлена влиянием на него факторов.
Чем ближе R2 к 1, тем выше качество модели.
Для оценки качества регрессионных моделей целесообразно использовать коэффициент множественной корреляции (индекс корреляции) R:
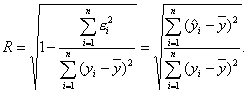 (3.13)
(3.13)
Данный коэффициент является универсальным, так как он отражает тесноту связи и точность модели, а также может использоваться при любой форме связи переменных.
При построении однофакторной модели и их линейной зависимости он равен коэффициенту линейной корреляции (R = |ry,x|).
Очевидно, что чем меньше влияние неучтенных факторов, тем лучше модель соответствует фактическим данным.
Также для оценки точности регрессионных моделей целесообразно использовать среднюю относительную ошибку аппроксимации:
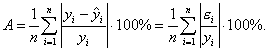 (3.14)
(3.14)
Чем меньше рассеяние эмпирических точек вокруг теоретической линии регрессии, тем меньше средняя ошибка аппроксимации. Ошибка аппроксимации меньше 7% свидетельствует о хорошем качестве модели.
После того как уравнение регрессии построено, выполняется проверка значимости построенного уравнения в целом и отдельных параметров.
Оценить значимость уравнения регрессии — это означает установить, соответствует ли математическая модель, выражающая зависимость между Y и X, фактическим данным и достаточно ли включенных в уравнение объясняющих переменных X для описания зависимой переменной Y.
Оценка значимости уравнения регрессии производится для того, чтобы узнать, пригодно уравнение регрессии для практического использования (например, для прогноза) или нет. При этом выдвигают основную гипотезу о незначимости уравнения в целом, которая формально сводится к гипотезе о равенстве нулю параметров регрессии, или, что то же самое, о равенстве нулю коэффициента детерминации: R2 = 0. Альтернативная ей гипотеза о значимости уравнения – гипотеза о неравенстве нулю параметров регрессии.
Для проверки значимости модели регрессии используется F-критерий Фишера, вычисляемый как отношение дисперсии исходного ряда и несмещенной дисперсии остаточной компоненты. Если расчетное значение с ν1 = k и ν2 = (n-k-1) степенями свободы, где k — количество факторов, включенных в модель, больше табличного при заданном уровне значимости, то модель считается значимой.
Для модели парной регрессии
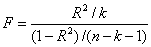 (3.15)
(3.15)
В качестве меры точности применяют несмещенную оценку дисперсии остаточной компоненты, которая представляет собой отношение суммы квадратов уровней остаточной компоненты к величине (n-k-1), где k — количество факторов, включенных в модель. Квадратный корень из этой величины (Sε) называется стандартной ошибкой оценки.
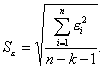 (3.16)
(3.16)
Для модели парной регрессии
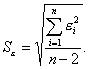
Анализ статистической значимости параметров модели парной регрессии:
yi = α + β × xi + εi.
Значения yi, соответствующие данным xi при теоретических значениях α и β являются случайными. Случайными являются и рассчитанные по ним значения коэффициентов α и β.
Надежность получаемых оценок α и β зависит от дисперсии случайных
отклонений (ошибок). По данным выборки эти отклонения и соответственно их
дисперсия не оцениваются — в расчетах используются отклонения зависимой
переменной yi от ее расчетных значений
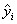 : εi = yi
– α – βxi. Так как ошибки (остатки) εi
нормально распределены, то среднеквадратическое отклонение ошибок используется
для измерения этой вариации. Среднеквадратические отклонения коэффициентов
известны как стандартные ошибки (отклонения):
: εi = yi
– α – βxi. Так как ошибки (остатки) εi
нормально распределены, то среднеквадратическое отклонение ошибок используется
для измерения этой вариации. Среднеквадратические отклонения коэффициентов
известны как стандартные ошибки (отклонения):
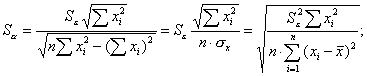
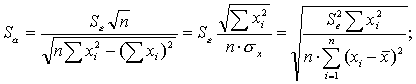 (3.17)
(3.17)
где 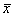 — математическое ожидание
независимой переменной х;
— математическое ожидание
независимой переменной х;
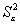 — стандартная ошибка, вычисляемая
по формуле (3.16);
— стандартная ошибка, вычисляемая
по формуле (3.16);
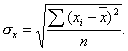
Проверка значимости отдельных коэффициентов регрессии связана с определением расчетных значений t-критерия (t-статистики) для соответствующих коэффициентов регрессии:
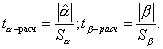 (3.18)
(3.18)
Затем расчетные значения tрасч сравниваются с табличными tтабл. Табличное значение критерия определяется при (n-2) степенях свободы (n — число наблюдений) и соответствующем уровне значимости α (0,1; 0,05).
Если расчетное значение t-критерия с (п-2) степенями свободы превосходит его табличное значение при заданном уровне значимости, коэффициент регрессии считается значимым. В противном случае фактор, соответствующий этому коэффициенту, следует исключить из модели (при этом ее качество не ухудшится).
Интервальная оценка параметров модели
Для значимого уравнения регрессии представляет интерес построение интервальных оценок для параметра α1
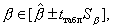 (3.19)
(3.19)
свободного члена α0
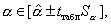
где tтабл определяется по таблице распределения Стьюдента для уровня значимости α и числа степеней свободы k = n-2;
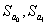 — стандартные отклонения
соответственно свободного члена и коэффициента модели (3.6);
— стандартные отклонения
соответственно свободного члена и коэффициента модели (3.6);
n — число наблюдений.
Прогнозирование с применением уравнения регрессии
Регрессионные модели могут быть использованы для прогнозирования возможных ожидаемых значений зависимой переменной.
Прогнозируемое значение переменной у получается при подстановке в уравнение регрессии
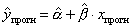 (3.18)
(3.18)
ожидаемой величины фактора х. Данный прогноз называется точечным. При выборе ожидаемой величины х нельзя подставлять значения независимой переменной хпрогн, значительно отличающиеся от входящих в исследуемую выборку, по которой вычислено уравнение регрессии.
Вероятность реализации точечного прогноза практически равна нулю. Поэтому рассчитывается средняя ошибка прогноза или доверительный интервал прогноза с достаточно большой надежностью.
Доверительные интервалы зависят от стандартной ошибки (3.15),
удаления хпрогн от своего среднего значения
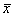 , количества наблюдений n и уровня
значимости прогноза α. В частности, для прогноза (3.18) будущие значения
упрогн с вероятностью (1-α) попадут в интервал
, количества наблюдений n и уровня
значимости прогноза α. В частности, для прогноза (3.18) будущие значения
упрогн с вероятностью (1-α) попадут в интервал
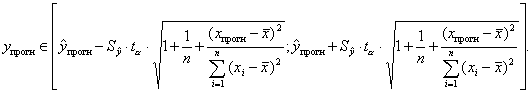
Пример 3.3.
Используя данные примера 3.2, оцените накопления семьи, имеющей доход 42 тыс. долл. и отобразите на графике исходные данные, результаты моделирования и прогнозирования.
Решение
В примере 3.2 была построена модель зависимости накопления от дохода:
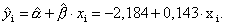
Для того чтобы определить накопления семьи при доходе в 42 тыс. долл. необходимо подставить значение хпрогн в полученную модель.
yпрогноз = -2,184 + 0,143 × 42 = 3,827.
Величину отклонения от линии регрессии вычисляют по формуле
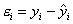 , используя данные таблицы 3.4. Величину
Sε находят по формуле (3.16):
, используя данные таблицы 3.4. Величину
Sε находят по формуле (3.16):
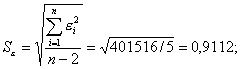
Таблица 3.4
| Наблюдение | Накопления Y | 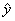 (предсказанное Y) (предсказанное Y)
|
Остатки, ε | ε2 |
|---|---|---|---|---|
| 1 | 3,0 | 3,541 | -0,5406 | 0,2923 |
| 2 | 6,0 | 5,688 | 0,3125 | 0,0977 |
| 3 | 5,0 | 4,256 | 0,7438 | 0,5532 |
| 4 | 3,5 | 2,109 | 1,3906 | 1,9338 |
| 5 | 1,5 | 2,109 | -0,6094 | 0,3713 |
| 6 | 4,5 | 4,972 | -0,4719 | 0,2227 |
| 7 | 2,0 | 2,825 | -0,8250 | 0,6806 |
| Сумма | 25,5 | 25,500 | 0,0000 | 4,1516 |
Коэффициент Стьюдента tα для m = 5 степеней свободы (m = n-2) и уровня значимости 0,1 равен 2,015.

Таким образом, прогнозное значение
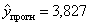 будет находиться между верхней границей,
равной 3,827 + 1,965 = 5,792 и нижней границей, равной 3,827 - 1,965 = 1,862.
будет находиться между верхней границей,
равной 3,827 + 1,965 = 5,792 и нижней границей, равной 3,827 - 1,965 = 1,862.
График исходных данных и результаты моделирования приведены на рис. 3.3.
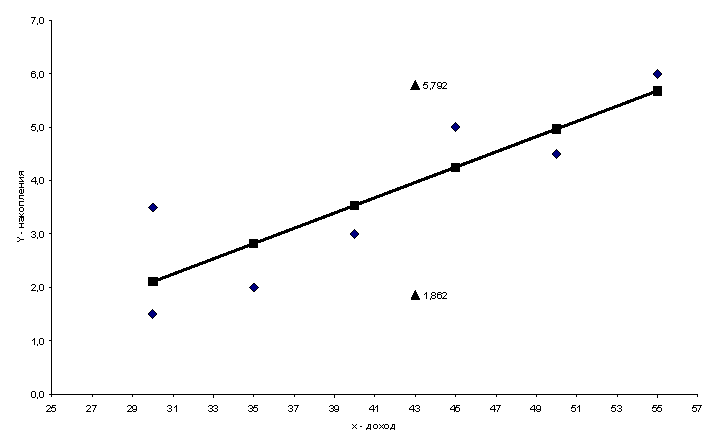
Рис. 3.3. График модели парной регрессии зависимости накопления от дохода
Нелинейная регрессия
Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций.
Теоретические вопросы, связанные с построением моделей нелинейной регрессии, следует изучить по учебнику «Эконометрика» под ред. И.И. Елисеевой (стр. 62-80).
Пример 3.4
По семи предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (Y, млн. руб.) от объема капиталовложений (X, млн. руб.).
| Y | 64 | 56 | 52 | 48 | 50 | 46 | 38 |
| X | 64 | 68 | 82 | 76 | 84 | 96 | 100 |
Требуется:
1. Для характеристики Y от X построить следующие модели:
• линейную (для сравнения с нелинейными),
• степенную,
• показательную,
• гиперболическую.
2. Оценить каждую модель, определив:
• индекс корреляции,
• среднюю относительную ошибку,
• коэффициент детерминации,
• F-критерий Фишера.
3. Составить сводную таблицу вычислений, выбрать лучшую модель, дать интерпретацию рассчитанных характеристик.
4. Рассчитать прогнозные значения результативного признака по лучшей модели, если объем капиталовложений составит 89,573 млн. руб.
5. Результаты расчетов отобразить на графике.
Решение
1. Построение линейной модели парной регрессии
Определим линейный коэффициент парной корреляции по следующей формуле:
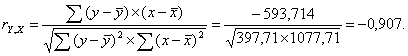
Можно сказать, что связь между объемом капиталовложений X и объемом выпуска продукции Y обратная, достаточно сильная.
Уравнение линейной регрессии имеет вид:
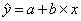 .
.
Таблица 3.5
| t | y | x | 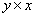 |
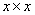 |
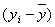 |
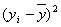 |
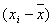 |
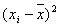 |
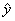 |
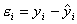 |
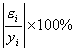 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 64 | 64 | 4096 | 4096 | 13,43 | 180,36 | -17,4 | 303,8 | 60,2 | 3,84 | 6,000 |
| 2 | 56 | 68 | 3808 | 4624 | 5,43 | 29,485 | -13,4 | 180,36 | 58,0 | -1,96 | -3,500 |
| 3 | 52 | 82 | 4264 | 6724 | 1,43 | 2,0449 | 0,57 | 0,3249 | 50,3 | 1,74 | 3,346 |
| 4 | 48 | 76 | 3648 | 5776 | -2,57 | 6,6049 | -5,43 | 29,485 | 53,6 | -5,56 | -11,583 |
| 5 | 50 | 84 | 4200 | 7056 | -0,57 | 0,3249 | 2,57 | 6,6049 | 49,2 | 0,84 | 1 680 |
| 6 | 46 | 96 | 4416 | 9216 | -4,57 | 20,885 | 14,57 | 212,28 | 42,6 | 3,44 | 7,478 |
| 7 | 38 | 100 | 3800 | 10000 | -12,6 | 158.0 | 18,57 | 344,84 | 40,4 | -2,36 | -6,211 |
| Итого | 354,00 | 570,00 | 28232 | 47492 | 0,01 | 397,71 | 1077,7 | -0,02 | 39,798 | ||
| ср. знач. | 50,57 | 81,43 | 4033,14 | 6784,57 | 5,685 | ||||||
| диспер. | 56,80 | 154,00 |
Значения параметров a и b линейной модели определим, используя данные таблицы 3.5.
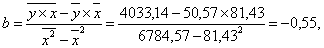
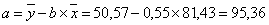
Уравнение линейной регрессии имеет вид:
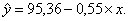
С увеличением объема капиталовложений на 1 млн. руб. объем выпускаемой продукции уменьшится в среднем на 550 тыс. руб. Это свидетельствует о неэффективности работы предприятий, и необходимо принять меры для выяснения причин и устранения этого недостатка.
Рассчитаем коэффициент детерминации:
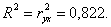
Вариация результата Y (объема выпуска продукции) на 82,2 % объясняется вариацией фактора X (объемом капиталовложений).
Оценку значимости уравнения регрессии проведем с помощью F-критерия Фишера:
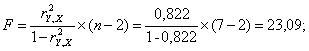
F > Fтабл = 6,61 для α = 0,05; k1 = m = 1, k2 = n – m – 1 = 5.
Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, т. к. F > Fтабл.
Определим среднюю относительную ошибку:
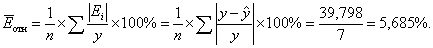
В среднем расчетные значения
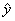 для линейной модели отличаются от фактических
значений на 5,685%.
для линейной модели отличаются от фактических
значений на 5,685%.
2. Построение степенной модели парной регрессии
Уравнение степенной модели имеет вид:
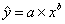 .
.
Для построения этой модели необходимо произвести линеаризацию
переменных. Для этого произведем логарифмирование обеих частей уравнения:
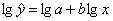 .
.
| Факт Y(t) | lg(Y) | Переменная X(t) | lg(X) | |
|---|---|---|---|---|
| 1 | 64,0 | 1,806 | 64 | 1,806 |
| 2 | 56,0 | 1,748 | 68 | 1,833 |
| 3 | 52,0 | 1,716 | 82 | 1,914 |
| 4 | 48,0 | 1,681 | 76 | 1,881 |
| 5 | 50,0 | 1,699 | 84 | 1,924 |
| 6 | 46,0 | 1,663 | 96 | 1,982 |
| 7 | 38,0 | 1,580 | 100 | 2,000 |
| 28 | 354,0 | 11,893 | 570 | 13,340 |
| Сред. знач. | 50,5714 | 1,699 | 81,429 | 1,906 |
Обозначим 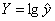 , X = lg
x, A = lg a.
, X = lg
x, A = lg a.
Тогда уравнение примет вид: Y = A + b X — линейное уравнение регрессии.
Рассчитаем его параметры, используя данные таблицы 3.6.
Таблица 3.6
| y | Y | x | X | YX | X2 | 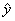 |
Ei | |Ei/y|×100% | 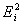 |
|
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 64 | 1,8062 | 64 | 1,8062 | 3,2623 | 3,2623 | 61,294 | 2,706 | 4,23 | 7,322 |
| 2 | 56 | 1,7482 | 68 | 1,8325 | 3,2036 | 3,3581 | 58,066 | -2,066 | 3,69 | 4,270 |
| 3 | 52 | 1,7160 | 82 | 1,9138 | 3,2841 | 3,6627 | 49,133 | 2,867 | 5,51 | 8,220 |
| 4 | 48 | 1,6812 | 76 | 1,8808 | 3,1621 | 3,5375 | 52,580 | -4,580 | 9,54 | 20,976 |
| 5 | 50 | 1 ,6990 | 84 | 1,9243 | 3,2693 | 3,7029 | 48,088 | 1,912 | 3,82 | 3,657 |
| 6 | 46 | 1,6628 | 96 | 1,9823 | 3,2960 | 3,9294 | 42,686 | 3,314 | 7,20 | 10,982 |
| 7 | 38 | 1,5798 | 100 | 2,0000 | 3,1596 | 4,0000 | 41,159 | -3,159 | 8,31 | 9,980 |
| Итого | 354 | 11,8931 | 13,3399 | 22,6370 | 25,4528 | 0,51 | 42,32 | 65,407 |
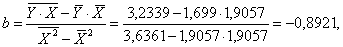
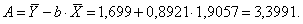
Уравнение регрессии будет иметь вид:
Y = 3,3991-0,8921 X.
Перейдем к исходным переменным х и у, выполнив потенцирование данного уравнения.
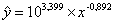
Получим уравнение степенной модели регрессии:
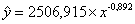 .
.
Определим индекс корреляции:
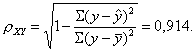
Связь между показателем y и фактором x можно считать достаточно сильной.
Коэффициент детерминации равен 0,836:
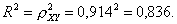
Вариация результата Y (объема выпуска продукции) на 83,6% объясняется вариацией фактора X (объемом капиталовложений).
Рассчитаем F-критерий Фишера:
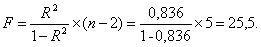
F > Fтабл = 6,61 для α = 0,05; k1 = m = 1, k2 = n – m – 1 = 5.
Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, т.к. F > Fтабл.
Средняя относительная ошибка
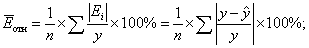
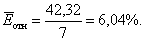
В среднем расчетные значения
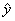 для степенной модели отличаются от фактических
значений на 6,04%.
для степенной модели отличаются от фактических
значений на 6,04%.
3. Построение показательной функции
Уравнение показательной кривой:
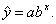
Для построения этой модели необходимо произвести линеаризацию переменных. Для этого осуществим логарифмирование обеих частей уравнения:
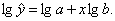
Обозначим: 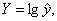 B = lg
b, A = lg a.
B = lg
b, A = lg a.
Получим линейное уравнение регрессии:
Y = A + B x.
Рассчитаем его параметры, используя данные таблицы 3.7.
Таблица 3.7
| t | y | Y | x | Yx | x2 | 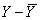 |
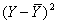 |
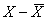 |
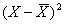 |
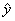 |
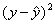 |
εi | |εi/yi|×100% |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 64 | 1,8062 | 64 | 115,60 | 4096 | 0,1072 | 0,0115 | -17,43 | 303,76 | 60,6 | 11,464 | 3,3859 | 5,290 |
| 2 | 56 | 1,7482 | 68 | 118,88 | 4624 | 0,0492 | 0,0024 | -13,43 | 180,33 | 58 | 3,9632 | -1,991 | 3,555 |
| 3 | 52 | 1,7160 | 82 | 140,71 | 6724 | 0,0170 | 0,0003 | 0,57 | 0,33 | 49,7 | 5,4221 | 2,3285 | 4,478 |
| 4 | 48 | 1,6812 | 76 | 127,77 | 5776 | -0,017 | 0,0003 | -5,43 | 29,47 | 53,1 | 25,804 | -5,08 | 10,583 |
| 5 | 50 | 1,6990 | 84 | 142,71 | 7056 | 0,0000 | 0,0000 | 2,57 | 6,61 | 48,6 | 2,0031 | 1,4153 | 2,831 |
| 6 | 46 | 1,6628 | 96 | 159,62 | 9216 | -0,036 | 0,0013 | 14,57 | 212,33 | 42,5 | 11,933 | 3,4544 | 7,509 |
| 7 | 38 | 1,5798 | 100 | 157,98 | 10000 | -0,119 | 0,0142 | 18,57 | 344,90 | 40,7 | 7,3132 | -2,704 | 7,117 |
| итого | 354 | 11,8931 | 570 | 963,28 | 4749 | 0,0300 | 1077,7 | 67,903 | 0,8093 | 41,363 | |||
| Сред. знач. | 50,57 | 1,6990 | 81,4 | 137,61 | 6785 | 5.909 |
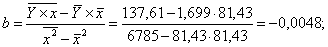
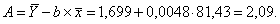
Уравнение будет иметь вид:
Y = 2,09 + 0,0048 x.
Перейдем к исходным переменным x и y, выполнив потенцирование данного уравнения:
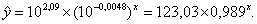
Определим индекс корреляции:
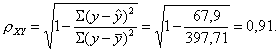
Связь между показателем y и фактором x можно считать тесной.
Индекс детерминации: 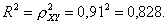
Вариация результата Y (объема выпуска продукции) на 41,1 % объясняется вариацией фактора X (объем капиталовложений).
Рассчитаем F-критерий Фишера:
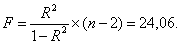
F > Fтабл = 6,61 для α = 0,05; k1 = m = 1, k2 = n – m – 1 = 5.
Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, т. к. F > Fтабл.
Средняя относительная ошибка:
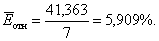
В среднем расчетные значения
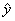 для линейной модели отличаются от фактических
значений на 5,909 %.
для линейной модели отличаются от фактических
значений на 5,909 %.
4. Построение гиперболической функции
Уравнение гиперболической функции:
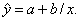
Произведем линеаризацию модели путем замены X = 1/x.
В результате получим линейное уравнение
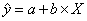 .
.
Рассчитаем его параметры по данным таблицы 3.8.
Таблица 3.8
| t | y | x | X | yX | X2 | 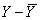 |
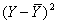 |
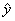 |
Ei | 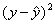 |
|εi/yi|×100% |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 64 | 64 | 0,0156 | 1,0000 | 0,0002441 | 13,43 | 180,33 | 61,5 | 2,489 | 6,1954 | 3,889 |
| 2 | 56 | 68 | 0,0147 | 0,8235 | 0,0002163 | 5,43 | 29,47 | 58,2 | -2,228 | 4,9637 | 3,978 |
| 3 | 52 | 82 | 0,0122 | 0,6341 | 0,0001487 | 1,43 | 2,04 | 49,3 | 2,740 | 7,5089 | 5,270 |
| 4 | 48 | 76 | 0,0132 | 0,6316 | 0,0001731 | -2,57 | 6,61 | 52,7 | -4,699 | 22,078 | 9,789 |
| 5 | 50 | 84 | 0,0119 | 0,5952 | 0,0001417 | -0,57 | 0,32653 | 48,2 | 1,777 | 3,1591 | 3,555 |
| 6 | 46 | 96 | 0,0104 | 0,4792 | 0,0001085 | -4,57 | 20,90 | 42.9 | 3,093 | 9,5648 | 6,723 |
| 7 | 38 | 100 | 0,0100 | 0,3800 | 0,0001000 | -12,57 | 158.04 | 41,4 | -3,419 | 11,69 | 8,997 |
| итого | 354 | 0,0880 | 4,5437 | 0,0011325 | 397,71 | 354,2 | -0,246 | 65,159 | 42,202 | ||
| Сред. знач. | 50,57 | 0,0126 | 0,6491 | 0,0001618 | 6,029 |
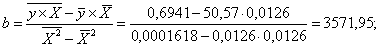
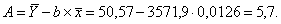
Получим следующее уравнение гиперболической модели:
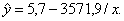
Определим индекс корреляции:
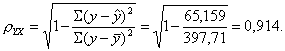
Связь между показателем у и фактором х можно считать достаточно сильной.
Индекс детерминации:
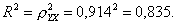
Вариация результата Y (объема выпуска продукции) на 83,5% объясняется вариацией фактора X (объемом капиталовложений).
F-критерий Фишера:
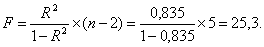
F > Fтабл = 6,61 для α = 0,05; k1 = m = 1, k2 = n – m – 1 = 5.
Уравнение регрессии с вероятностью 0,95 в целом не является статистически значимым, т. к. F > Fтабл.
Определим среднюю относительную ошибку:
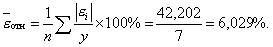
В среднем расчетные значения
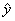 для линейной модели отличаются от фактических
значений на 6,029 %.
для линейной модели отличаются от фактических
значений на 6,029 %.
Для выбора лучшей модели построим сводную таблицу результатов.
Таблица 3.9
| Параметры | Коэффициент детерминации R2 | F-критерий Фишера | Индекс корреляции ρYX (rYX) | Средняя относительная ошибка Eотн |
|---|---|---|---|---|
| Модель | ||||
| Линейная | 0,822 | 23,09 | 0,907 | 5,685 |
| Степенная | 0,828 | 24,06 | 0,910 | 6,054 |
| Показательная | 0,828 | 24,06 | 0,910 | 5,909 |
| Гиперболическая | 0,835 | 25,30 | 0,914 | 6,029 |
Все модели имеют примерно одинаковые характеристики, но большее значение F-критерия Фишера и большее значение коэффициента детерминации R2 имеет гиперболическая модель. Ее можно взять в качестве лучшей для построения прогноза.
Расчет прогнозного значения результативного показателя
Прогнозное значение результативного признака (объема выпуска продукции) определим по уравнению гиперболической модели, подставив в него планируемую (заданную по условию) величину объема капиталовложений:
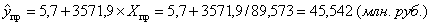
Построение парной нелинейной регрессии можно осуществить при помощи программы «Олимп: СтатЭксперт». Для этого необходимо выполнить следующую последовательность действий.
- Инициализировать программу, указать включение макросов, щелкнуть ОК.
- Ввести исходные данные - результативный признак (у) и факторный признак (х).
- В конец строки для «у» дописать 0, в конец строки для «х» - планируемое (заданное в условии) значение этого фактора (объема капиталовложений).
- Выделить этот блок данных.
- В меню СтатЭкс выбрать функцию Регрессия.
- Установить шаблон данных: указать ориентацию таблицы либо по строкам, либо по столбцам в зависимости от того, как был осуществлен ввод данных и наличие наименований таблицы, наблюдений. Щелкнуть Установить.
- В окне Регрессионный анализ в список выбранных переменных добавить два показателя, соответствующих значениям «у» и «х».
- Осуществить выбор зависимой переменной, для этого щелкнуть Выбор и выбрать показатель, соответствующий значениям «у». Установить.
- Определить прогнозирование по модели, указав шаг прогнозирования 1 и вероятность расчетов 80 %. Отключить режим ретропрогноза.
- Установить вид регрессии - Парная. Вычислить.
- В окне формирования набора моделей в списке доступных переменных выбрать гиперболическую модель у = а + b/х. Выход.
После выполнения этой последовательности действий программа осуществит расчет параметров гиперболической модели, прогнозных значений и построение графиков. Отчет по вычислениям представлен в следующем виде:
Таблица функций парной регрессии
| Функция | Критерий | Эластичность |
|---|---|---|
| Y(X)=+5,664+3571,928/X | 13,030 | 0,8856 |
| Выбрана функция Y(X)=+5,664+3571,928/X |
Таблица остатков
| Номер | Факт | Расчет | Ошибка абс. | Ошибка относит. | Фактор X |
|---|---|---|---|---|---|
| 1 | 64,000 | 61,476 | 2,524 | 3,944 | 64,000 |
| 2 | 56,000 | 58,193 | -2,193 | -3,916 | 68,000 |
| 3 | 52,000 | 49,225 | 2,775 | 5,337 | 82,000 |
| 4 | 48,000 | 52,663 | -4,663 | -9,716 | 76,000 |
| 5 | 50,000 | 48,187 | 1,813 | 3,625 | 84,000 |
| 6 | 46,000 | 42,872 | 3,128 | 6,800 | 96,000 |
| 7 | 38,000 | 41 ,384 | -3,384 | -8,904 | 100,000 |
Таблица характеристики остатков
| Характеристика | Значение |
|---|---|
| Среднее значение | 0,000 |
| Дисперсия | 9,307 |
| Приведенная дисперсия | 13,030 |
| Средний модуль остатков | 2,926 |
| Относительная ошибка | 6,035 |
| Критерий Дарбина-Уотсона | 2,891 |
| Критерий адекватности | 34,776 |
| Критерий точности | 54,475 |
| Критерий качества | 49,550 |
| Уравнение значимо с вероятностью 0,95 |
На основании данных расчетов получено уравнение гиперболической модели:
Y(X) = +5,664+3571,928/Х.
Аналогичные результаты были получены при осуществлении расчетов в Excel.
Фактические, расчетные и прогнозные значения по лучшей модели отобразим на рис. 3.4.
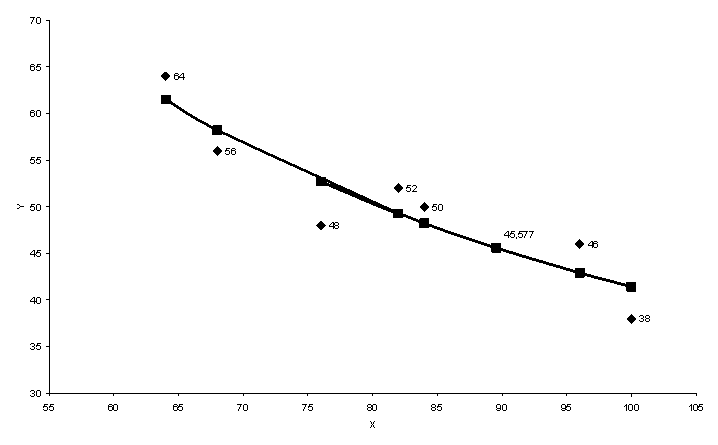
Рис. 3.4. Прогноз по лучшей модели
1 Основоположниками теории корреляции считаются английские биометрики Ф. Гальтон (1822-1911) и К. Пирсон (1857-1936). Термин «корреляция» был заимствован из естествознания и обозначает соотношение, соответствие. Представление о корреляции как об отношении взаимозависимости между случайными переменными величинами лежит в основе математико-статистической теории корреляции.