Часть I. Компьютерный практикум
Часть I. Компьютерный практикум
Пакет Excel содержит программу (надстройку) Поиск решения, позволяющую реализовывать модели линейной, нелинейной и дискретной оптимизации.
Если в меню Сервис отсутствует команда Поиск решения необходимо выполнить следующие действия:
- выбрать команду Сервис/Надстройки;
- в диалоговом окне Надстройки установить флажок Поиск решения;
- щелкнуть ОК.
После этого в меню Сервис появится новая команда Поиск решения.
1. Задача линейного программирования (ЗЛП), компьютерная реализация стандартными офисными средствами (в среде пакета Excel)
Оптимизационные (экстремальные) модели в экономике возникают при практической реализации принципа оптимальности в управлении [12].
Выбор оптимального управленческого поведения в конкретной производственной ситуации связан с проведением экономико-математического моделирования и решением задачи оптимального программирования, в простейшем случае - задачи линейного программирования.
В наиболее общем виде задача (модель) линейного программирования записывается следующим образом: требуется найти максимум (или минимум) линейной целевой функции
f(x1, x2, …, xn) = c1x1 + c2x2 + … + cnxn
при ограничениях
a11x1 + a12x2 + … + a1nxn {≤, =, ≥} b1
a21x2 + a22x2 + … + a2nxn {≤, =, ≥} b2
…
am1x1 + am2x2 + … + amnxn {≤, =, ≥} bm
xj ≥ 0, j = 1, 2, …, n,
где aij, bi, cj (i = 1, 2, ..., m, j = 1, 2, ..., n) - заданные постоянные величины.
Иногда невозможно получить решение по оптимизационной модели: область допустимых решений может оказаться пустым множеством (система ограничений задачи противоречива) или целевая функция является неограниченной на области определения.
Первый случай связан с некорректностями в постановке экономической задачи и (или) разработанной ЭММ. Например, имеющимся объемом ресурсов заведомо невозможно выполнить даже те минимальные объемы работ, которые закладываются в ограничения как необходимые минимальные плановые задания. Если в данной ситуации все же необходимо найти решение задачи, то следует построить непустое множество допустимых решений, исключив одно или несколько ограничений, т.е. фактически соблюсти принцип альтернативности.
Второй случай обычно означает, что ЭММ разработана некорректно, и некоторые существенные ограничения в ней отсутствуют.
1.1. Технология компьютерной реализации ЗЛП
Первым шагом при работе с командой (программой, надстройкой) Сервис/Поиск решения является создание специального (рабочего) листа, т.е. специальная запись ЭММ в терминах электронной таблицы (ЭТ) Excel [8,10,18].
Для этого необходимо создать в рабочем листе Excel целевую ячейку, в которой записывается целевая функция модели, а также одну или несколько изменяемых (переменных) ячеек, которые, как правило, отвечают управляющим переменным в модели и значения которых могут изменяться для достижения экстремума (максимума или минимума) целевой функции. Для успешного поиска решения необходимо, чтобы каждая из переменных ячеек влияла на целевую ячейку (другими словами, формула в целевой ячейке должна опираться в вычислениях на значения переменных ячеек). В противном случае при выполнении команды Поиск решения появляется сообщение об ошибке Результаты целевой ячейки не сходятся.
Ограничения модели определяются с помощью значений соответствующих ячеек, которые должны находиться в определенных пределах или удовлетворять граничным условиям. Ограничения могут налагаться как на целевую, так и на переменные ячейки (по два ограничения для каждой изменяемой ячейки с указанием верхнего и нижнего пределов, а также до ста дополнительных). Таким образом, на специальном листе должны содержаться ячейки, в которых вычисляются ограничиваемые величины. Тип каждого из ограничений модели (≤, =, ≥) задается (вводится) в специальном окне диалога при выполнении команды Поиск решения. Численные значения самих ограничений включать в специализированный лист необязательно - они также вводятся в специальном окне диалога при выполнении команды Поиск решения. В режиме Параметры окна диалога Поиск решения задается тип модели (линейная или нелинейная).
После команды Выполнить диалогового окна Поиск решения осуществляется поиск оптимального решения - в итоге появляется диалоговое окно Результаты поиска решения.
В режиме Справки этого диалогового окна содержатся сведения об итоговых сообщениях процедуры поиска решения. Например, в случае несовместности системы ограничений Excel будет выдавать сообщение Поиск не может найти подходящего решения. Если же решение задачи отсутствует вследствие неограниченности целевой функции на множестве допустимых решений, то Excel будет выдавать сообщение Значения целевой ячейки не сходятся. При успешном завершении решения задачи появляется диалоговое окно Результат поиска решения. Решение найдено. С помощью рубрики Результаты этого диалогового окна можно получить отчет по результатам решения, рубрики Устойчивость и Пределы позволяют провести дополнительный экономико-математический анализ оптимального плана и получить отчеты по устойчивости и по пределам.
1.2. Примеры задач линейного программирования
Задача линейного программирования в том или ином виде интерпретируется как задача об оптимальном использовании ограниченных производственных ресурсов. Приведем два варианта возможных постановок этой экономической задачи.
В первом примере приводится подробное описание технологии получения оптимального решения средствами Excel, во втором примере раскрываются лишь основные технологические этапы.
Пример 1. Задача об оптимальном использовании ограниченных ресурсов. Фабрика имеет в своем распоряжении определенное количество производственных ресурсов: трудовые, денежные средства, сырье, оборудование, производственные площади и т.п. Допустим, например, ресурсы трех видов - трудовые, сырье и оборудование имеются в количестве соответственно 80 чел./дней, 480 кг, 130 станко/часов. Фабрика может выпускать ковры четырех видов. Информация о количестве единиц каждого ресурса, необходимых для производства одного ковра каждого вида (о нормах расхода производственных ресурсов), и доходах, получаемых предприятием от реализации единицы каждого вида товаров, приведена в следующей таблице.
Таблица
| Ресурсы | Нормы расхода ресурсов на единицу изделия | Наличие ресурсов | |||
|---|---|---|---|---|---|
| ковер А | ковер В | ковер С | ковер D | ||
| Труд | 7 | 2 | 2 | 6 | 80 |
| Сырье | 5 | 8 | 4 | 3 | 480 |
| Оборудование | 2 | 4 | 1 | 8 | 130 |
| Цена (тыс. руб.) | 3 | 4 | 3 | 1 | |
Требуется составить такой план выпуска продукции, при котором будет получен максимальный доход от реализации продукции (сбыт всей выпущенной продукции обеспечен).
Экономико-математическая модель
Обозначим через X1, X2, X3, X4 объемы производства соответствующего вида продукции (количество ковров каждого типа).
Целевая функция - это математическая запись критерия оптимальности, т.е. выражение, которое необходимо максимизировать f(x) = 3X1 + 4X2 + 3X3 + X4.
Ограничения по ресурсам:
7X1 + 2X2 + 2X3 + 6X4 ≤ 80
5X1 + 8X2 + 4X3 + 3X4 ≤ 480
2X1 + 4X2 + X3 + 8X4 ≤ 130
X1, X2, X3, X4 ≥ 0
Решение. Приведем подробное описание технологии получения решения приведенной ЗЛП.
Обозначим: M1 - один щелчок левой кнопки мыши; М2 - двойной щелчок левой кнопки мыши.
Прежде чем приступить к решению задачи студенту необходимо на сервере создать папку под своим именем. Порядок работы:
- На рабочем столе найдите пиктограмму «Сетевое окружение» → М2.
- Двойным щелчком мыши открывайте пиктограмму «Для документов».
- Двойным щелчком мыши открывайте пиктограмму «Для студентов».
- В папке с фамилией ведущего преподавателя создайте папку под своей фамилией.
Далее необходимо последовательно выполнить следующую работу.
- Создать форму для ввода условий задачи. Запустите Excel, выбрав Microsoft Excel из подменю Программы главного меню Windows. Открывается чистый лист Excel. Создайте текстовую форму - таблицу для ввода условий задачи (рис. 1.1).
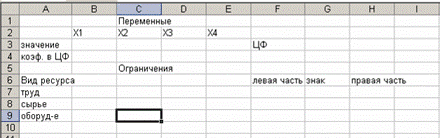
Рис. 1.1

Рис. 1.2
- Указать адреса ячеек, в которые будет помещен результат решения (изменяемые ячейки). Обозначьте через X1, X2, X3, X4 количество ковров каждого типа. В нашей задаче оптимальные значения компонент вектора X = (X1, X2, X3, X4) будут помещены в ячейках В3:Е3, оптимальное значение целевой функции — в ячейке F4.
- Ввести исходные данные задачи в созданную форму—таблицу, представленную на рис. 1.2. Сохраните таблицу, т.к. она должна быть представлена в отчете по лабораторной работе.
Порядок сохранения таблицы следующий.
В строке Меню указатель мыши на имя Файл → M1. В развернутом меню команда Сохранить как → M1. Появляется диалоговое окно Сохранение документа. Путем перебора папок в строке Папка должна быть установлена папка с фамилией студента. Далее курсор переведите в строку Имя файла и присвойте ему имя. Далее нажать кнопку Сохранить.
- Ввести зависимость для целевой функции:
- курсор в ячейку F4.
- курсор на кнопку «Мастер функций», расположенную на панели инструментов.
- M1. На экране появляется диалоговое окно Мастер функций шаг 1 из 2 (рис. 1.3).
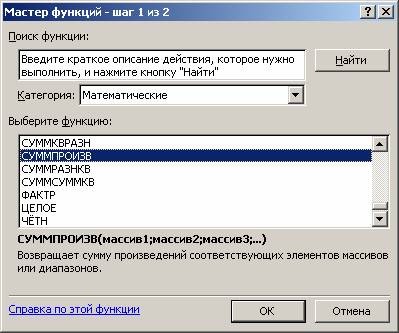
Рис. 1.3
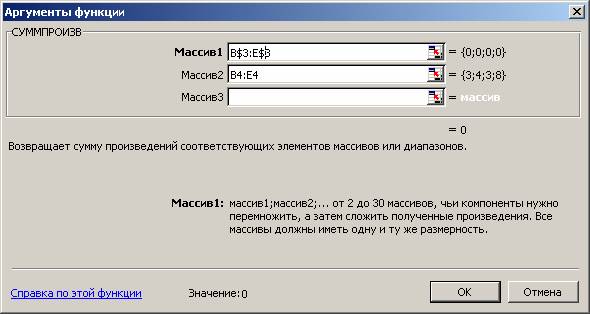
Рис. 1.4
- курсор в окно «Категория» на категорию Математические;
- M1;
- курсор в окно Функции на СУММПРОИЗВ;
- M1. На экране появляется диалоговое окно СУММПРОИЗВ (рис. 1.4);
- в строку «Массив 1» ввести В$3:Е$3;
- в строку «Массив 2» ввести В4:Е4;
- кнопка «ОК». На экране: в ячейку F4 введена функция (рис. 1.4).
Примечание: Адреса ячеек во все диалоговые окна удобно вводить не с клавиатуры, а протаскивая мышь по ячейкам, чьи адреса следует ввести.
- Ввести зависимости для ограничений:
- курсор в ячейку F4;
- на панели инструментов кнопка Копировать в буфер → M1;
- курсор в ячейку F7;
- на панели инструментов кнопка Вставить из буфера → M1;
- курсор в ячейку F8;
- на панели инструментов кнопка Вставить из буфера → M1;
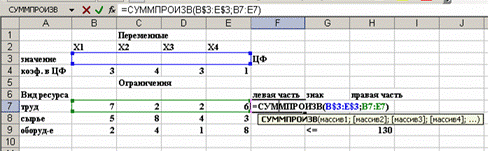

Рис. 1.5
- курсор в ячейку F9;
- на панели инструментов кнопка Вставить из буфера → M1.
Примечание. Содержимое ячеек F7-F9 необходимо проверить. Они обязательно должны содержать информацию, как это показано для примера на рис. 1.5 (в качестве примера представлено содержимое ячейки F7).
В строке Меню указатель мыши на имя Сервис → M1. В развернутом меню команда Поиск решения → M1. Появляется диалоговое окно Поиск решения (рис. 1.6).
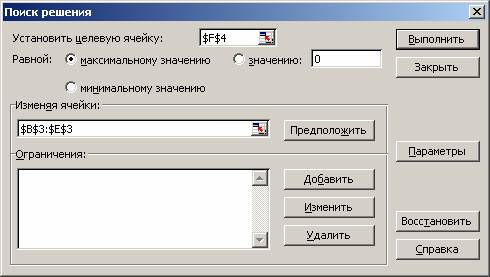
Рис. 1.6
- Назначить целевую функцию (установить целевую ячейку):
- курсор в строку Установить целевую ячейку;
- введите адрес ячейки $F$4;
- введите направление целевой функции в зависимости от условия вашей задачи - Максимальному значению или Минимальному значению);
- курсор в строку Изменяя ячейки;
- введите адреса искомых переменных В$3:Е$3.
- Ввести ограничения:
- указатель мышки на кнопку Добавить → M1. Появляется диалоговое окно Добавление ограничения (рис. 1.7);
- в строке Ссылка на ячейку введите адрес $F$7;
- введите знак ограничения ≤;
- в строке Ограничение введите адрес $Н$7;
- указатель мыши на кнопку Добавить → M1. На экране вновь диалоговое окно Добавление ограничения (рис. 1.7).
- введите остальные ограничения задачи, по вышеописанному алгоритму;
- после введения последнего ограничения кнопка ОК.
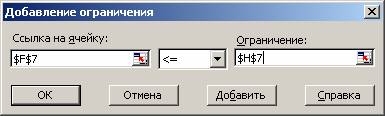
Рис. 1.7
На экране появится диалоговое окно Поиск решения с введенными условиями (рис. 1.8).
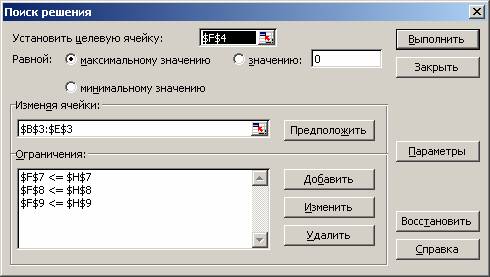
Рис. 1.8
- Ввести параметры для решения ЗЛП:
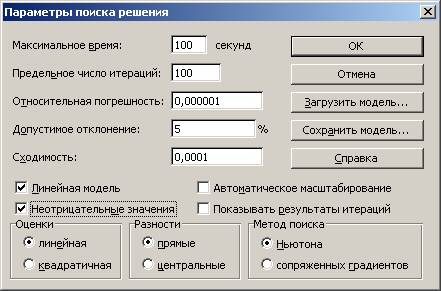
Рис. 1.9
- установите флажки в окнах Линейная модель (это обеспечит применение симплекс-метода) и Неотрицательные значения;
- указатель мыши на кнопку ОК. На экране диалоговое окно Поиск решения;
- указатель мыши на кнопку Выполнить.
Через непродолжительное время появится диалоговое окно Результаты поиска решения и исходная таблица с заполненными ячейками В3:Е3 для значений Xi и ячейка F4 с максимальным значением целевой функции (рис. 1.10).
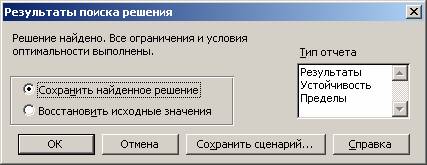
Рис. 1.10
Полученное решение означает, что максимальный доход 150 тыс. руб. фабрика может получить при выпуске и реализации 30 ковров второго вида и 10 ковров третьего вида. При этом трудовые ресурсы и фонд рабочего времени оборудования будут использованы полностью, а из 480 кг пряжи (ресурс «сырье») будет использовано 280 кг.
Пример 2. Задача об оптимальном использовании ограниченных ресурсов. На участок строящейся дороги необходимо вывезти 20000 м3 каменных материалов. В районе строительства имеются три карьера с запасами 8000 м3, 9000 м3 и 10000 м3. Для погрузки материалов используются экскаваторы, имеющие производительность 250 м3/смену в карьерах А, Б и 500 м3/смену в карьере В. Эти карьеры обеспечивают каменными материалами также ряд других строящихся объектов. На погрузку материалов для рассматриваемого участка выделен для экскаваторов общий лимит 60 машино-смен с правом использовать его по усмотрению строителей. Транспортные затраты на перевозку материалов характеризуются следующими показателями: на перевозку 1000 м3 материалов из карьера А требуется 100 автомобиле-смен, из карьера Б - 135 автомобиле-смен, из карьера В - 170 автомобиле-смен.
Требуется составить оптимальный план перевозок, обеспечивающий минимальные транспортные затраты.
Экономико-математическая модель
Для удобства записи модели примем за единицу измерения количества материалов 10000 м3. Обозначим через х1 объем добычи материалов в карьере А, х2 - в карьере Б, х3 — в карьере В. С учетом сказанного математически задача может быть записана следующим образом:
min f(x1, x2, x3) = 1000x1 + 1350х2 + 1700х3
при ограничениях:
x1 + x2 + x3 = 2,0
40х1 + 40х2 + 20x3 ≤ 60
0 ≤ x1 ≤ 0,8
0 ≤ х2 ≤ 0,9
0 ≤ х3 ≤ 1,0.
Решение. Приведенная ЭММ является моделью задачи линейного программирования (ЗЛП). Она может быть реализована симплекс-методом. Получим решение средствами пакета Excel. Ниже на рис. 1.11 приведена одна из возможных форм специального листа (рабочей таблицы) для рассматриваемой модели.
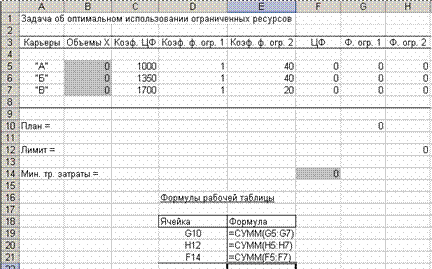
Рис. 1.11
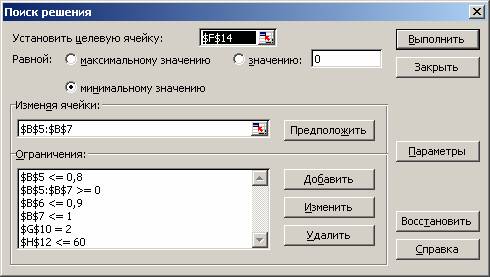
Рис. 1.12. Диалоговое окно Поиск решения
На рабочем листе не показаны промежуточные формулы для ячеек F5:F7, G5:G7, H5:H7, которые являются произведением изменяемых ячеек для X и соответствующих ячеек для коэффициентов ЦФ и функциональных ограничений. После команды Сервис/Поиск решения необходимо оформить диалоговое окно как это показано на рис. 1.12.
После нажатия клавиши Выполнить в диалоговом окне Поиск решения осуществляется реализация модели. Ниже в таблице приведены результаты решения задачи.
ЗАДАЧА ОБ ОПТИМАЛЬНОМ ИСПОЛЬЗОВАНИИ ОГРАНИЧЕННЫХ РЕСУРСОВ
| Карьер | Объем X | Коэф. ЦФ | Коэф.ф. огр.-1 | Коэф.ф. огр.- 2 | ЦФ | Ф.огр.-1 | Ф.огр.- 2 |
|---|---|---|---|---|---|---|---|
| А | 0,8 | 1000 | 1 | 40 | 800 | 0,8 | 32 |
| Б | 0,2 | 1350 | 1 | 40 | 270 | 0,2 | 8 |
| В | 1,0 | 1700 | 1 | 20 | 1700 | 1,0 | 20 |
| План | 2 | ||||||
| Лимит | 60 | ||||||
| Мин. тр. затраты | 2770 | ||||||
То есть оптимальные значения переменных х1 = 0,8; х2 = 0,2; x3 = 1,0. Таким образом, из карьера А следует вывезти 8000 м3, из карьера Б - 2000 м3, из карьера В - 10000 м3 каменных материалов. При этом транспортные затраты будут минимальны и равны 2770 автомобиле-смен.
1.3. Специальные задачи линейного программирования, примеры компьютерной реализации
Ниже приводятся примеры специальных ЗЛП - транспортной задачи и задачи о назначениях, которая интерпретируется как частный случай транспортной задачи (в разделе 2.2 задача о назначениях рассматривается как пример задачи дискретной оптимизации).
Пример. Перед менеджером нефтяной компании «Магнум» стоит задача создания схемы поставки нефтепродуктов от четырех нефтеперерабатывающих комплексов компании к пяти регионам страны. Одним из основных условий поставленной задачи является минимизация стоимости перевозок, при этом все мощности нефтеперерабатывающих комплексов должны быть реализованы и все потребности регионов должны быть удовлетворены.
Мощности поставщиков и мощности потребителей, а также стоимость перевозок нефтепродуктов представлены в следующей таблице (в условных единицах).
| Мощности поставщиков | Мощности потребителей | ||||
|---|---|---|---|---|---|
| 600 | 400 | 700 | 500 | 1000 | |
| 700 | 4 | 8 | 5 | 1 | 6 |
| 800 | 3 | 5 | 2 | 3 | 4 |
| 900 | 2 | 6 | 5 | 4 | 3 |
| 800 | 1 | 4 | 3 | 5 | 3 |
Экономико-математическая модель
В данном случае мощности поставщиков нефтепродуктов и потребности регионов в них совпадают, т.е. имеем дело с закрытой моделью транспортной задачи (см., например, [12]).
Решение. Ввод условий задачи состоит из следующих основных этапов.
- Создание формы для решения задачи.
- Ввод граничных условий.
- Ввод исходных данных.
- Назначение целевой функции.
- Ввод зависимостей из математической модели.
- Ввод ограничений.
- Просмотр результатов и печать отчета.
Рассмотрим более подробно каждый из этих этапов.
- Создание формы для решения задачи предполагает создание матрицы перевозок.
Для этого необходимо выполнить резервирование изменяемых ячеек: в блок ячеек B3:F6 вводится «1».
Таким образом, резервируется место, где после решения задачи будет находиться распределение поставок, обеспечивающее минимальные затраты на перевозку груза (нефтепродуктов).
- Ввод граничных условий.
Введение условия реализации мощностей поставщиков, т.е.
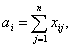
где ai - мощность i-го поставщика;
xij — объем поставки груза от i-го поставщика к j-му потребителю;
n — количество потребителей.
Для этого необходимо выполнить следующие операции:
- курсор в ячейку A3;
- щелкнуть знак «∑»;
- выделить необходимые для суммирования ячейки B3:F3;
- нажать ENTER - подтверждение ввода формулы для суммирования.
Аналогичные действия выполнить для ячеек А4, А5, А6, т.е. ввести условия реализации мощностей всех поставщиков (для всех строк). Эти действия можно реализовать иначе:
- курсор в A3;
- копировать в буфер (т.е. копировать в буфер формулу, введенную для ячейки A3);
- выделить ячейки А4:А6;
- вставить из буфера (вставка формулы для суммирования в А4:А6).
Введение условия удовлетворения запросов потребителей, т.е.
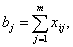
где b – мощность j-го потребителя;
m - количество поставщиков.
Для этого необходимо выполнить следующие операции:
- курсор в В7;
- щелкнуть знак «∑ ». При этом автоматически выделяется весь столбец В3:В6;
- ENTER - подтверждение суммирования показателей выделенного столбца.
Последовательность этих действий выполнить для ячеек C7-F7, или же:
- курсор в В7;
- копировать в буфер;
- выделить С7:F7;
- вставить из буфера.
Таким образом, введены ограничения для всех поставщиков и всех потребителей.
- Ввод исходных данных.
В конкретном примере осуществляется ввод мощностей четырех нефтеперерабатывающих предприятий (ячейки А11:А14), потребности регионов в их продукции (B10:F10), а также удельные затраты по доставке нефтепродуктов от конкретного поставщика потребителю (блок B11:F14) (рис. 1.13).
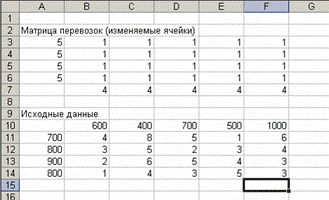
Рис. 1.13. Ввод исходных данных и граничных условий
- Назначение целевой функции.
Для вычисления значения целевой функции, соответствующей минимальным суммарным затратам на доставку груза, необходимо зарезервировать ячейку и ввести формулу для ее вычисления:
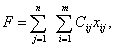
где Сij — стоимость доставки единицы груза от i-го поставщика к j-му потребителю;
xij — объем поставки груза от i-го поставщика к j-му потребителю.
Для этого:
- курсор в ячейку В15. В данную ячейку будет помещаться значение целевой функции после решения задачи;
- щелкнуть Мастер функций (значок fx);
- в окне Категория выбрать Математические;
- в окне Функция при помощи спинера выбрать СУММПРОИЗВ;
- ОК;
- в окне СУММПРОИЗВ указать адреса массивов, элементы которых обрабатываются этой функцией.
В задаче целевая функция представляет собой произведение удельных затрат на доставку груза (расположенных в блоке ячеек B11:F14) и объемов поставок для каждого потребителя (содержимое ячеек B3:F6). Для этого:
- в поле Массив 1 указать адреса B11:F14;
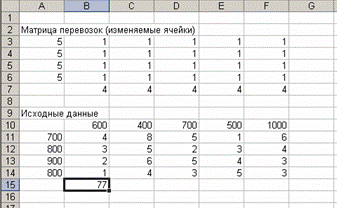
Рис. 1.14. Назначение целевой функции
- в поле Массив 2 указать адреса B3:F6;
- OK - подтверждение окончания ввода адресов массивов.
В поле ячейки В15 появится некоторое числовое значение, равное произведению единичных поставок на удельные коэффициенты затрат по доставке грузов (число 77 в данной задаче, рис. 1.14).
- Ввод зависимостей из математической модели.
Для осуществления этого этапа необходимо выполнить следующий перечень операций:
- щелкнуть Сервис - Поиск решения;
- курсор подвести в поле Установить целевую (ячейку);
- ввести адрес $В$15. Таким образом производится указание ячейки, куда при решении задачи помещается значение целевой функции (или же: курсор в В15, затем щелкнуть Поиск решения. При этом осуществится автоматический ввод адреса $В$15 в поле адреса целевой ячейки);
- установить направление изменения целевой функции, равное «минимальному значению»;
- ввести адреса изменяемых ячеек B3:F6. Для этого:
- щелкнуть в поле изменяя ячейки;
- ввести адреса $B$3:$F$6 ( или же щелкнуть на маленькой красной стрелке рядом с этим полем, выйти в таблицу с матрицей перевозок, выделить блок ячеек B3:F6, щелкнуть на красной стрелке и вернуться в блок Поиска решения, при этом нужные адреса будут введены).
Ввести ограничение задачи. В матрицу перевозок, содержащую исходные данные по задаче, необходимо ввести условие реализации мощностей всех поставщиков. Для этого:
- щелкнуть Добавить ограничения;
- в поле Ссылка на ячейку ввести адреса $А$3:$А$6;
- в среднем поле установить знак " = ". Для этого щелкнуть спикер и выбрать необходимый знак " = ".
- в поле Ограничение установить адреса $А$11:$А$14.
- щелкнуть ОК, т.е. осуществить подтверждение введенного условия. После этого Вы вернетесь в поле Поиск решения.
Далее вводится ограничение, которое реализует условие удовлетворения мощностей всех потребителей. Для этого:
- щелкнуть Добавить ограничение;
- в поле Ссылка на ячейку ввести адреса $B$7:$F$7;
- в поле знака выбрать при помощи спинера знак " = ";
- в поле Ограничение (третье поле) установить адреса $B$10:$F$10;
- ОК (рис. 1.15).
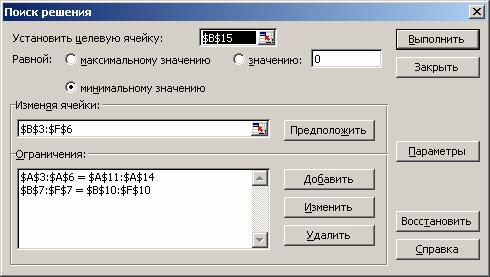
Рис. 1.15. Ввод зависимостей из математической модели
- Ввод ограничений.
Далее необходимо установить ограничения на решение задачи. Для этого:
- щелкнуть Параметры;
- установить Линейная модель;
- установить Неотрицательные значения, так как объемы поставок груза отрицательной величиной быть не могут (рис. 1.16);
- ОК. После этого осуществится выход в поле Поиска решений;
- нажать Выполнить.
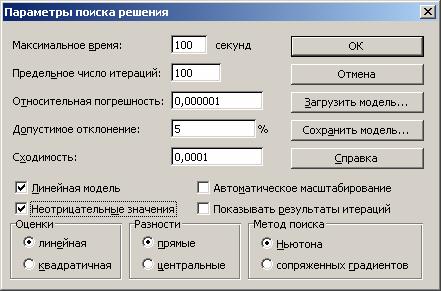
Рис. 1.16. Установление параметров задачи
- Просмотр результатов и печать отчета.
После выполнения всех вышеуказанных действий на экран выводится окно Результаты поиска решения (рис. 1.17).
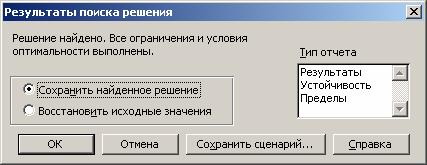
Рис. 1.17. Решение найдено
- В окне Тип отчета выбрать интересующий вид отчета.
- ОК.
- Внизу страницы экрана содержится сообщение Отчет по результатам 1. Щелкнуть на этом сообщении, на экран выводятся результаты решения задачи, которые можно распечатать.
При нажатии Лист 1 происходит возврат в программу к исходным данным.
В матрице перевозок содержатся оптимальные объемы поставок грузов от поставщика потребителям, дающие минимум затрат на доставку. Значение целевой функции содержится в ячейке В15 и для конкретной задачи равно 7800 (рис. 1.18).
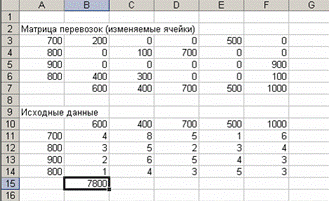
Рис. 1.18. Задача решена
Из вышеизложенного можно сделать следующий вывод: минимум затрат на доставку нефтепродуктов, равный 7800 условных денежных единиц, будет обеспечен при следующем плане поставок:
- от первого поставщика первому потребителю в объеме 200 единиц и четвертому в объеме 500 единиц (условных);
- от второго поставщика второму потребителю в объеме 100 единиц и третьему потребителю в объеме 700 единиц (условных);
- от третьего поставщика пятому потребителю в объеме 900 единиц (условных);
- от четвертого поставщика первому потребителю в объеме 400 единиц и второму потребителю в объеме 300 единиц (условных).
При данной схеме поставок мощности всех поставщиков будут реализованы и спросы всех потребителей будут удовлетворены.
Рассмотрим задачу о назначениях, которая в этом случае интерпретируется и реализуется как частный случай транспортной задачи.
Пример. На коммерческом предприятии имеется m работников A1, А2, ..., Ai, ..., Аm, каждый из которых может выполнять одну из имеющихся m видов работ: В1, В2, ..., Вj, ..., Вm. Известно, что один и тот же работник может выполнять разливные виды работ с разной производительностью труда (Сij) в зависимости от опыта работы, квалификации, индивидуальных особенностей. В связи с этим возникает проблема распределения работников по должностям таким образом, чтобы производительность труда в коллективе была максимальной.
Экономико-математическая модель.
Обозначим через xij назначение i-го работника на j-должность. Так как количество работников равно количеству должностей и один работник может занимать только одну должность, то xij может принимать только два значения: 1 (если работник назначается на данную должность) или 0 (если не назначается). Тогда суммарная производительность труда работников (целевая функция) имеет следующий вид:
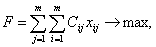
при ограничениях
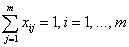
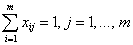
xij ≥ 0, i = 1, …, m; j = 1, …, m,
Умножая целевую функцию на -1, задача распределения по должностям может быть приведена к транспортной задаче, в которой объем запасов каждого поставщика и объем потребностей каждого потребителя равны 1.
Числовой пример. Перед менеджером фирмы «Стар» стоит задача распределения четырех работников по вакантным должностям по условиям результатов контрольных испытаний. Производительность труда по отдельным видам работ, показанная каждым из работников, приведена в таблице.
Одним из основных условий поставленной задачи является максимизация производительности труда в коллективе при условии, что каждый работник может быть назначен только на одну работу.
| Работники | Производительность труда работников по должностям | |||
|---|---|---|---|---|
| B1 | В2 | B3 | В4 | |
| А1 | 3 | 1 | 5 | 2 |
| А2 | 2 | 4 | 8 | 6 |
| А3 | 8 | 2 | 7 | 6 |
| А4 | 4 | 3 | 5 | 1 |
Решение. Ввод условий задачи состоит из следующих основных этапов:
- Создание формы для решения задачи.
- Ввод граничных условий.
- Ввод исходных данных.
- Назначение целевой функции.
- Ввод зависимостей из математической модели.
- Ввод ограничений.
- Просмотр результатов и печать отчета.
Рассмотрим более подробно каждый из этих этапов.
- Создание формы для решения задачи предполагает создание матрицы назначений по должностям.
Для этого необходимо выполнить резервирование изменяемых ячеек: в блок ячеек В3:Е6 вводятся «1».
Таким образом, резервируется место, где после решения задачи будет находиться распределение рабочих по должностям, обеспечивающее максимальную производительность труда.
- Ввод граничных условий.
Введение условия назначения работника только на одну должность, т.е.
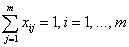
где хij — назначение i-го работника на j-ую должность;
m — количество вакантных должностей.
Для этого необходимо выполнить следующие операции:
- курсор в ячейку A3;
- щелкнуть знак «∑»;
- выделить необходимые для суммирования ячейки В3:Е3;
- нажать ENTER - подтверждение ввода формулы для суммирования.
Аналогичные действия выполнить для ячеек А4, А5, А6, т.е. ввести условия реализации мощностей всех поставщиков (для всех строк). Эти действия можно реализовать иначе:
- курсор в A3;
- копировать в буфер (т.е. копировать в буфер формулу, введенную для ячейки A3);
- выделить ячейки А4:А6;
- вставить из буфера (вставка формулы для суммирования в А4:А6).
Введение условия заполнения вакантной должности, т.е.
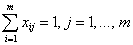
Для этого необходимо выполнить следующие операции:
- курсор в В7;
- щелкнуть знак «∑». При этом автоматически выделяется весь столбец В3:В6;
- ENTER - подтверждение суммирования показателей выделенного столбца.
Последовательность этих действий выполнить для ячеек C7:F7, или же:
- курсор в В7;
- копировать в буфер;
- выделить С7:Е7;
- вставить из буфера.
Таким образом, введены ограничения по назначению работника только на одну должность и условию заполнения всех вакантных мест.
- Ввод исходных данных.
В конкретном примере осуществляется ввод условной мощности работника фирмы (в ячейки А11:А14 вводится «1»), потребности в заполнении вакантной должности («1» - в В10:Е10), ввод производительности труда конкретного работника при проведении контрольных испытаний по каждой должности (блок В11:Е14) (рис. 1.19).
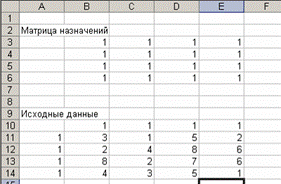
Рис. 1.19. Ввод исходных данных
- Назначение целевой функции.
Для вычисления значения целевой функции, соответствующей максимальной суммарной производительности труда, необходимо зарезервировать ячейку и ввести формулу для ее вычисления:
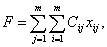
где Сij — производительность труда i-го работника при занятии j-й должности;
xij - назначение i-го работника на j-должность.
Для этого:
- курсор в ячейку В16. В данную ячейку будет помещаться значение целевой функции после решения задачи;
- щелкнуть Мастер функций (значок fx);
- в окне Категория выбрать Математические;
- в окне Функция при помощи спинера выбрать СУММПРОИЗВ;
- OK;
- в окне СУММПРОИЗВ указать адреса массивов, элементы которых обрабатываются этой функцией.
В задаче целевая функция представляет собой произведение производительности труда работников (расположенных в блоке ячеек В11:В14) и назначения работников на должности (содержимое ячеек В3:Е6). Для этого:
- в поле Массив 1 указать адреса В11:E14;
- в поле Массив 2 указать адреса В3:Е6;
- ОК - подтверждение окончания ввода адресов массивов.
В поле ячейки В16 появится некоторое числовое значение, равное произведению «1» на производительность каждого работника на конкретной должности (число 67 в данной задаче) (рис. 1.20).
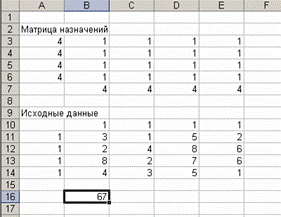
Рис. 1.20. Назначение целевой функции
- Ввод зависимостей из математической модели.
Для осуществления этого этапа необходимо выполнить следующий перечень операций:
- щелкнуть Сервис - Поиск решения;
- курсор подвести в поле Установить целевую (ячейку);
- ввести адрес $В$16. Таким образом производится указание ячейки, куда при решении задачи помещается значение целевой функции (или же: курсор в В16, затем щелкнуть Поиск решения. При этом осуществится автоматический ввод адреса $В$16 в поле адреса целевой ячейки);
- установить направление изменения целевой функции, равное «максимальному значению»;
- ввести адреса изменяемых ячеек В3:Е6. Для этого:
- щелкнуть в поле Изменяя ячейки;
- ввести адреса $В$3:$Е$6 (или же щелкнуть на маленькой красной стрелке рядом с этим полем, выйти в таблицу с матрицей перевозок, выделить блок ячеек В3:Е6, щелкнуть на красной стрелке и вернуться в блок Поиск решения, при этом нужные адреса будут введены).
- Ввести ограничение задачи. В матрицу перевозок, содержащую исходные
данные по задаче, необходимо ввести условие назначения работника только
на одну должность. Для этого:
- щелкнуть Добавить ограничения;
- в поле Ссылка на ячейку ввести адреса $А$3:$А$6;
- в среднем поле установить знак " = ". Для этого щелкнуть спинер и выбрать необходимый знак " = ";
- в поле Ограничение установить адреса $А$11:$А$14;
- щелкнуть ОК, т.е. осуществить подтверждение введенного условия. После этого Вы вернетесь в поле Поиск решения.
Далее вводится ограничение, которое реализует условие заполнения вакантной должности. Для этого:
- щелкнуть Добавить ограничение;
- в поле Ссылка на ячейку ввести адреса $В$7:$Е$7;
- в поле знака выбрать при помощи спинера знак " = ";
- в поле Ограничение (третье поле) установить адреса $В$10:$Е$10;
- ОК (рис. 1.21).
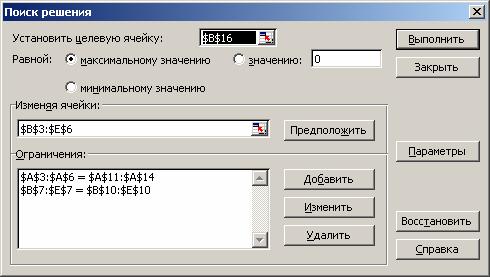
Рис. 1.21. Ввод зависимостей из математической модели
- Ввод ограничений.
Далее необходимо установить ограничения на решение задачи. Для этого:
- щелкнуть Параметры;
- установить Линейная модель;
- установить Неотрицательные значения (назначение работника на должность принимает значение «1» или «0» , т.е. отрицательной величиной быть не может);
- ОК. После этого осуществится выход в поле Поиск решения;
- нажать Выполнить.
- Просмотр результатов и печать отчета.
После выполнения всех вышеуказанных действий на экран выводится окно Результаты поиска решения.
- В окне Тип отчета выбрать интересующий вид отчета;
- ОК;
- Внизу страницы экрана содержится сообщение Отчет по результатам 1. Щелкнуть на этом сообщении, на экран выводятся результаты решения задачи, которые можно распечатать.
При нажатии Лист 1 происходит возврат в программу к исходным данным.
В Матрице назначений содержится схема распределения работников по должностям (1 - назначен, 0 - не назначен), дающая максимальную суммарную производительность труда. Значение целевой функции содержится в ячейке В16 и для конкретной задачи равно 22 (рис. 1.22).
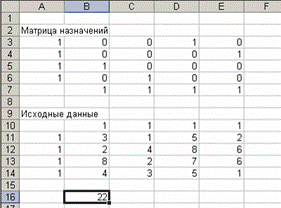
Рис. 1.22. Задача решена
Вывод: максимум производительности труда, равный 22 условных единицы, будет достигнут при назначении:
- первого работника на должность В3 (содержимое ячейки D3 равно 1);
- второго работника на должность В4 («1» в ячейке Е4);
- третьего работника на должность В1 («1» в ячейке В5);
- четвертого работника на должность В2 («1» в ячейке С6).
2. Модели нелинейной и дискретной оптимизации, компьютерная реализация стандартными офисными средствами (в среде пакета Excel)
Рассмотрим некоторые примеры нелинейных и дискретных типовых оптимизационных экономических задач, их экономико-математические модели и методы компьютерной реализации в среде пакета Excel.
2.1. Особенности компьютерной реализации
Задача (модель) нелинейного программирования (НЛП) формулируется так же, как и общая задача оптимального программирования со следующими требованиями к целевой функции (ЦФ) и допустимой области: ЦФ f(х1, х2, ..., хn) и (или) одна из функций gi (x1, х2, ..., хn) являются нелинейными:
min(max) f(x1, x2, …, xn)
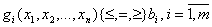
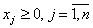
У произвольной задачи НЛП некоторые или все свойства, характерные для задач ЛП, отсутствуют [12]. Вследствие этого задачи НЛП несравнимо сложнее задач ЛП, и для них не существует общего универсального метода их решения (аналогично симплексному методу).
Есть целый ряд методов решения задач НЛП, некоторые из них рассмотрены в [12]. В пакете Excel реализован [8] метод множителей Лагранжа, идея которого заключается в преобразовании задачи условной оптимизации в задачу безусловной оптимизации, решение которой производится методами поиска - градиентными методами (методы первого порядка) или методами Ньютона (методы второго порядка). Наиболее распространенными являются градиентные методы.
Следует, на наш взгляд, согласиться с Б.Курицким [8], что для практического решения задачи оптимизации суть этих методов знать не обязательно.
Однако необходимо помнить, что существующие методы дают возможность находить только локальные оптимумы (помимо случаев, когда задачи обладают соответствующими свойствами выпуклости и вогнутости [7,12]). Если же есть подозрение, что в допустимой области ЦФ может иметь несколько оптимумов, то эту область следует разбить на ряд областей и в каждой из них определить свои локальные оптимумы, а затем из всех локальных оптимумов выбрать глобальный. В таком практическом подходе задача поиска глобального оптимума сводится к решению ряда задач, в которых ищется свой (локальный) оптимум.
Следует отметить, что в подавляющем большинстве практических задач оптимизации существует только один оптимум [8].
Решение задачи НЛП (реализация модели нелинейной оптимизации) средствами Excel отличается от решения ЗЛП следующим:
- назначаются начальные значения искомых переменных
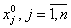 так, чтобы ЦФ в начальной точке не
была равна нулю,
так, чтобы ЦФ в начальной точке не
была равна нулю, 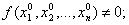
- в диалоговом окне Поиск решения в режиме Параметры не надо вводить Линейная модель.
В Excel признаком достижения оптимума является величина относительного
приращения ЦФ на каждой итерации 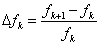 . Оптимум
считается достигнутым, если выполняется условие Δfk
≤ Δfзад, где Δfзад - точность, назначаемая
при решении задачи (Параметры).
. Оптимум
считается достигнутым, если выполняется условие Δfk
≤ Δfзад, где Δfзад - точность, назначаемая
при решении задачи (Параметры).
Примером задачи НЛП является модель оптимального формирования портфеля ценных бумаг (модель Марковица минимального риска).
В этой модели приняты следующие обозначения [17]:
xj,
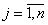 - доля капитала, потраченная на покупку
ценных бумагу j-го вида (весь выделенный капитал принимается за 1);
- доля капитала, потраченная на покупку
ценных бумагу j-го вида (весь выделенный капитал принимается за 1);
mj — средняя ожидаемая доходность
j-й ценной бумаги, 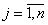 (mj
называют эффективностью j-й ценной бумаги);
(mj
называют эффективностью j-й ценной бумаги);
νj - дисперсия случайной доходности
j-й ценной бумаги, 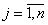 (
(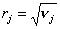 называют риском j-й ценной бумаги).
называют риском j-й ценной бумаги).
В предположении о некоррелированности ценных бумаг (их независимости) модель Марковица имеет вид:
Найти xj,
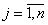 , минимизирующие риск портфеля ценных
бумаг
, минимизирующие риск портфеля ценных
бумаг
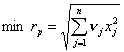 (2.1)
(2.1)
при условии, что обеспечивается заданное значение эффективности портфеля mp, т.е.
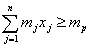 (2.2)
(2.2)
и условии, что весь выделенный для инвестиций капитал в целях моделирования принимается за 1, т.е.
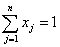 (2.3)
(2.3)
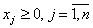 (2.4)
(2.4)
В модели (2.1)-(2.4) нелинейной является ЦФ.
Задачи оптимизации, в результате решения которых искомые значения переменных должны быть целыми числами, называются задачами (моделями) целочисленного (дискретного) программирования:
min(max) f(x1, x2, …, xn)
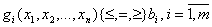
xj - целые неотрицательные
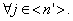
Если множество индексов 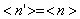 =
{1, 2, ..., n}, то задачу называют полностью целочисленной, если
=
{1, 2, ..., n}, то задачу называют полностью целочисленной, если
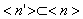 , то - частично целочисленной.
, то - частично целочисленной.
Существуют различные методы решения задач дискретного программирования (дискретной оптимизации). Наиболее часто используемым методом является метод ветвей и границ. Именно этот метод реализован в программе Поиск решения пакета Excel.
Дискретная оптимизация средствами Excel проводится аналогично решению соответствующих непрерывных задач. Основное отличие заключается во вводе при оформлении диалогового окна Поиск решения требования целочисленности соответствующих переменных (при этом в режиме Параметры устанавливается тип задачи - линейная или нелинейная).
Исходя из требования целочисленности в случае дискретной оптимизации возможен вызов только одного Отчета по результатам.
Достаточно часто при моделировании экономических процессов используется особый случай дискретности задачи - булевость переменных, т.е. переменные могут принимать значения 0 или 1. Характерным примером этого случая является задача о назначениях (приводится в качестве примера задачи дискретной оптимизации и для иллюстрации механизма учета в Excel булевости переменных).
Пример 1. Имеется n видов работ и n исполнителей
этих работ. Известны экономические оценки эффекта Сij,
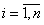 ,
, 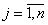 от
назначения i-го исполнителя на j-й вид работ. Распределите
исполнителей по видам работ так, чтобы суммарный эффект от назначений был
максимальным.
от
назначения i-го исполнителя на j-й вид работ. Распределите
исполнителей по видам работ так, чтобы суммарный эффект от назначений был
максимальным.
Экономико-математическая модель
Введем необходимые обозначения, пусть
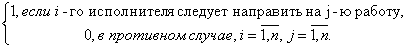
Тогда математически задачу о назначениях можно записать в виде:
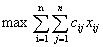
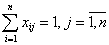 (на каждую работу должен
быть назначен исполнитель)
(на каждую работу должен
быть назначен исполнитель)
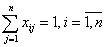 (все исполнители должны получить
назначение)
(все исполнители должны получить
назначение)
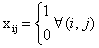 (*)
(*)
Для реализации этой ЭММ средствами Excel ограничение (*) в рабочей таблице Excel следует записать в виде:
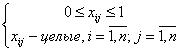
Этот прием используется во всех дискретных задачах с булевыми переменными.
Отметим некоторые особые случаи приведенной задачи.
1. Если по той или иной причине некоторое назначение является недопустимым, то соответствующий элемент матрицы (Сij)n×n принимается равным (-М), т.е. его значение заведомо меньше любого другого значения. После этого в ходе решения мы сможем избежать данного назначения автоматически.
2. Если матрица (Сij)n×n
не является квадратной, то по аналогии открытой транспортной задачи в модели
задачи о назначениях следует записать либо ограничение
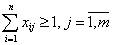 (число исполнителей m больше числа
работ n), или
(число исполнителей m больше числа
работ n), или 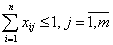 (число исполнителей
m меньше числа работ n).
(число исполнителей
m меньше числа работ n).
Рассмотрим некоторые типовые задачи (модели) нелинейной и дискретной оптимизации.
2.2. Примеры задач нелинейной и дискретной оптимизации
В примере 1 приводится подробное описание технологии получения оптимального решения задачи дискретной оптимизации средствами Excel, в остальных примерах раскрываются лишь основные технологические этапы.
Пример 2. Задача производства неделимой продукции (оптимизация производственной программы мебельного предприятия). Мебельное предприятие выпускает три вида наборов мебели, книжные полки и тумбу под телевизоры. Характеристики каждого вида продукции приведены в таблице 2.1. При условии получения максимальной прибыли объем товарной продукции должен составить не менее 459,31 тыс. руб. Ситуация со сбытом продукции сложилась следующая. Книжными полками рынок насыщен, поэтому торговые организации уменьшили объем договоров до 10 тыс. шт. Тумбы для телевизоров могут быть реализованы в объемах от 4 до 7 тыс. шт., наборы мебели 2 - от 7 до 10 тыс. шт. Спрос на наборы мебели 1 и 3 неограничен и требуется не менее 10 тыс. шт. Предприятие имеет технологическое оборудование, число единиц которого и нормы затрат времени оборудования каждой группы на изготовление единицы каждого вида продукции приведены в табл. 2.2. Предприятие работает в две смены с эффективным временем работы каждой машины в 3945 ч. (коэффициент сменности 1,9). Оптимизируйте производственную программу предприятия (составьте план выпуска продукции, максимизирующий прибыль предприятия).
Таблица 2.1
| Показатель, тыс. руб. | Вид продукции | ||||
|---|---|---|---|---|---|
| набор мебели 1 | набор мебели 2 | набор мебели 3 | книжные полки | тумба под телевизор | |
| Оптовая цена единицы изделия | 7,2 | 14,3 | 26,9 | 0,243 | 1,5 |
| Прибыль от реализации | 2,4 | 4,5 | 8,9 | 0,081 | 0,45 |
Таблица 2.2
| Наименование оборудования | Число, шт. | Вид продукции | ||||
|---|---|---|---|---|---|---|
| набор мебели 1 | набор мебели 2 | набор мебели 3 | книжные полки | тумба под телевизор | ||
| Линия раскроя древесно-стружечных плит | 2 | 0,068 | 0,096 | 0,207 | 0,018 | 0,042 |
| Гильотинные ножницы | 1 | 0,045 | 0,080 | 0,158 | 0,011 | 0,035 |
| Линия облицовывания | 2 | 0,132 | 0,184 | 0,428 | 0,020 | 0,060 |
| Линия обрезания кромок | 2 | 0,057 | 0,082 | 0,230 | 0,010 | 0,028 |
| Лаконаливная машина | 2 | 0,063 | 0,090 | 0,217 | 0,010 | 0,032 |
| Полировальные станки | 4 | 0,170 | 0,280 | 0,620 | 0,020 | 0,096 |
Экономико-математическая модель.
Обозначим через X1, Х2, Х3, Х4, Х5 объем продукции каждого типа (шт.).
Каждая машина работает в две смены с эффективным временем работы 3945 ч. Определим фонд времени работы оборудования каждого типа:
| линия раскроя древесно-стружечных плит | 2 x 3945 = 7890 ч; |
| гильотинные ножницы | 1 х 3945 = 3945 ч; |
| линия облицовывания | 2 x 3945 = 7890 ч; |
| линия обрезания кромок | 2 x 3945 = 7890 ч; |
| лаконаливная машина | 2 x 3945 = 7890 ч; |
| полировальные станки | 4 x 3945 = 15780 ч; |
Целевая функция — математическая запись критерия оптимальности
"максимум прибыли от реализации", т.е. необходимо максимизировать f(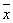 )
= 2,4X1 + 4,5Х2 + 8,9X3
+ 0,06X4 + 0,45X5.
)
= 2,4X1 + 4,5Х2 + 8,9X3
+ 0,06X4 + 0,45X5.
Ограничение по объему товарной продукции:
7,2X1 + 14,3X2 +26,9X3 + 0,243X4 + 1,5X5 ≥ 459,31 тыс. руб.
Ограничения по фонду времени работы оборудования:
0,068X1 + 0,096X2 + 0,207X3 + 0,018X4 + 0,042X5 ≤ 7890
0,045X1 + 0,080X2 + 0,158X3 + 0,011X4 + 0,035X5 ≤ 7890
0,132X1 + 0,184X2 + 0,428X3 + 0,020X4 + 0,060X5 ≤ 3945
0,057X1 + 0,082X2 + 0,230X3 + 0,010X4 + 0,028X5 ≤ 7890
0,063X1 + 0,090X2 + 0,217X3 + 0,010X4 + 0,033X5 ≤ 7890
0,170X1 + 0,280X2 + 0,620X3 + 0,020X4 + 0,096X5 ≤ 15780
Ограничения по сбыту продукции:
X1 ≥ 10000
7000 ≤ X2 ≤ 10000
X3 ≥ 10000
X4 ≤ 10000
4000 ≤ X4 ≤ 7000
X1, X2, X3, X4, X5 ≥ 0
X1, X2, X3, X4, X5 целые.
Решение. Подготовим рабочий лист Excel (рис. 2.1).
Основные этапы получения оптимального решения отражены на рис. 2.2-2.4.
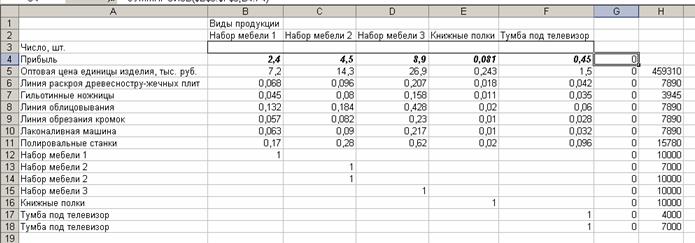
Рис. 2.1. Рабочий лист с введенными данными
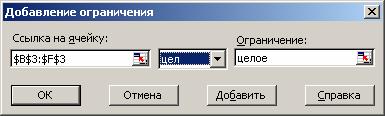
Рис. 2.2. Введение ограничений целочисленности переменных
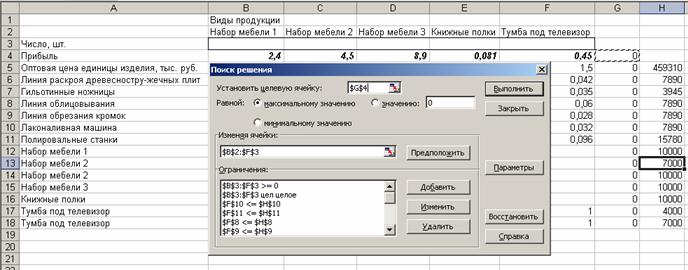
Рис. 2.3. Введены все условия для решения задачи
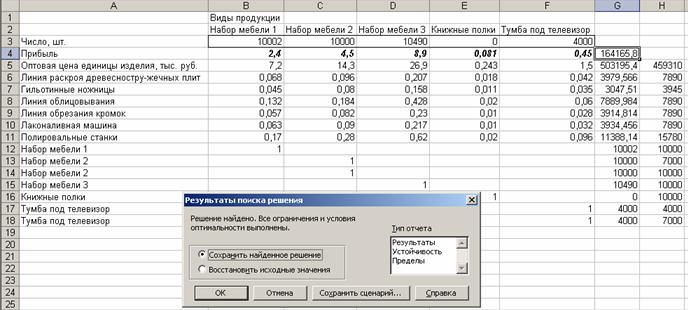
Рис. 2.4. Решение найдено. Все ограничения и условия оптимальности выполнены
Таблица 2.3.
РЕЗУЛЬТАТЫ ПОИСКА ПРЕДСТАВЛЕНЫ РЕЗУЛЬТАТЫ ПОИСКА ОПТИМАЛЬНОГО РЕШЕНИЯ ЗАДАЧИ
| Виды продукции | |||||||
|---|---|---|---|---|---|---|---|
| набор мебели 1 | набор мебели 2 | набор мебели 3 | книжные полки | тумба под телевизор | |||
| Число, шт. | 10002 | 10000 | 10490 | 0 | 4000 | ||
| Прибыль | 2,4 | 4,5 | 8,9 | 0,081 | 0,45 | 164166 | |
| Ограничения | Левая часть | Правая часть | |||||
| Оптовая цена единицы изделия, тыс. руб. | 7,2 | 14,3 | 26,9 | 0,243 | 1,5 | 503195,4 | 459310 |
| Линия раскроя древесно-стружечных плит | 0,068 | 0,096 | 0,207 | 0,018 | 0,042 | 3979,566 | 7890 |
| Гильотинные ножницы | 0,045 | 0,08 | 0,158 | 0,011 | 0,035 | 3047,51 | 3945 |
| Линия облицовывания | 0,132 | 0,184 | 0,428 | 0,02 | 0,06 | 7889,984 | 7890 |
| Линия обрезания кромок | 0,057 | 0,082 | 0,23 | 0,01 | 0,028 | 3914,814 | 7890 |
| Лаконаливная машина | 0,063 | 0,09 | 0,217 | 0,01 | 0,032 | 3934,456 | 7890 |
| Полировальные станки | 0,17 | 0,28 | 0,62 | 0,02 | 0,096 | 11388,14 | 15780 |
| Набор мебели 1 | 1 | 10002 | 10000 | ||||
| Набор мебели 2 | 1 | 10000 | 7000 | ||||
| Набор мебели 2 | 1 | 10000 | 10000 | ||||
| Набор мебели 3 | 1 | 10490 | 10000 | ||||
| Книжные полки | 1 | 0 | 10000 | ||||
| Тумба под телевизор | 1 | 4000 | 4000 | ||||
| Тумба под телевизор | 1 | 4000 | 7000 | ||||
Выводы. Для получения максимальной прибыли необходимо произвести: наборов мебели 1 вида 10002 шт., наборов мебели 2 вида 10000 шт., наборов мебели 3 вида 10490 шт., тумбы под телевизор 4000 шт. Книжные полки в этом месяце не следует производить.
Задача о ранце. В терминах задачи о ранце (рюкзаке) формулируются многие задачи загрузки в некоторую емкость тех или иных предметов.
Пример 3. Организация арендует баржу грузоподъемностью 83 т, на которой предполагает перевозить груз, состоящий из предметов четырех типов. Веса и стоимости предметов равны соответственно 24 т, 22 т, 16 т, 10 т и 96 у.е., 85 у.е., 50 у.е., 20 у.е. Требуется погрузить на баржу груз максимальной стоимости.
Экономико-математическая модель
Введем необходимые обозначения: пусть хj (j = 1,2,3,4) — число предметов j-го типа, которое следует погрузить на баржу. Тогда ЭММ задачи о подборе для баржи допустимого груза максимальной ценности запишется следующим образом:
max f(x1, х2, х3, х4) = 96х1 + 85х2 + 50х3 + 20х4,
24x1 + 22х2 + 16х3 + 10х4 ≤ 83,
хj (j = 1,2,3,4) - целые неотрицательные.
Решение. Приведенная ЭММ является моделью задачи целочисленного линейного программирования (ЦЛП). Для реализации этой модели средствами Excel в диалоговом окне режима Поиск решения с помощью кнопки Добавить следует ввести ограничение целочисленности переменных (целые числа в изменяемых ячейках). Специализированный (рабочий) лист может быть подготовлен в виде, представленном на рис. 2.5. Формулы этого листа очевидны. Диалоговое окно, отвечающее приведенному выше рабочему листу, представлено на рис. 2.5.
Результаты реализации разработанной ЭММ приведены ниже в таблице
Таблица 2.4
РЕЗУЛЬТАТЫ РЕШЕНИЯ ЗАДАЧИ О РАНЦЕ
| Тип груза | Коэф.цел.ф. | Коэф.ф.огр. | Цел.ф-ция | Ф-ция огр-я | Перем.з-чи |
|---|---|---|---|---|---|
| А | 96 | 24 | 288 | 72 | 3 |
| В | 85 | 22 | 0 | 0 | 0 |
| С | 50 | 16 | 0 | 0 | 0 |
| D | 20 | 10 | 20 | 10 | 1 |
| Грузоподъемность | 82 | ||||
| MaxF | 308 |
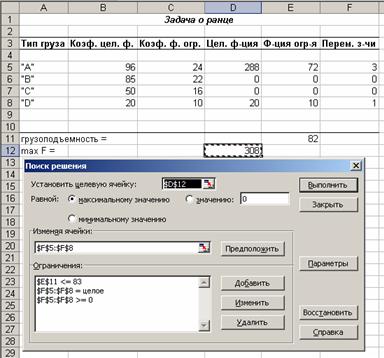
Рис. 2.5. Начальная рабочая таблица и диалоговое окно
Таким образом, рекомендуемое управленческое решение с позиций принятого критерия оптимальности — следует погрузить три предмета первого типа и один предмет четвертого типа. В этом случае стоимость груза составит 308 у.е., и одна тонна грузоподъемности будет не использована (ее можно использовать на другие цели).
Пример 4. Задача о рациональном раскрое строительных материалов. Часть заемных оборотных средств предприятия иммобилизована в запасы пиломатериалов: на складе имеется партия бруса, содержащая 300 штук длиной 7,5 м каждый и партия бруса, содержащая 500 штук длиной 5 м каждый. Из этого материала можно изготовить оконные блоки, в каждый из которых входит две детали по 2,5 м и три детали длиной 2 м каждая. Как оптимально использовать заемные средства, если предположить, что спрос на оконные рамы неограничен?
Экономико-математическая модель
Оконный блок - некоторый комплект продукции или ассортиментный набор (2, 3). Понятно, что в этой задаче о раскрое критерий оптимальности - «максимум выпуска (реализации) комплектной продукции».
Построим возможные способы (карты) раскроя исходного материала, с этой целью составим таблицу:
| Брус 7,5 м | Брус 5,0 м | ||||||
|---|---|---|---|---|---|---|---|
| 2,5 м | 2,0 м | Отходы | 2,5 м | 2,0 м | Отходы | ||
| X11(y1) | 3 | 0 | 0 | Х21(y5) | 2 | 0 | 0 |
| Х12(y2) | 2 | 1 | 0,5 | Х22(y6) | 1 | 1 | 0,5 |
| Х13(y3) | 1 | 2 | 1,0 | X23(y7) | 0 | 2 | 1,0 |
| Х14(y4) | 0 | 3 | 1,5 | ||||
Введем необходимые обозначения: xij - число брусьев из i-й партии (i = 1, 2), которое следует раскроить j-м способом.
Рассмотрим соотношения:
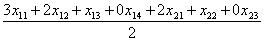
и
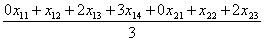
Обозначим через Z - минимальное из этих соотношений (это и будет количество комплектной, ассортиментной продукции). С учетом этого ЭММ имеет вид - max Z при ограничениях:
x11 + х12 + х13 + х14 = 300,
х21 + х22 + х23 = 500,
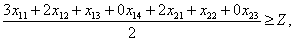
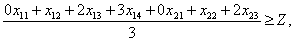
xij, Z - целые неотрицательные.
Решение. Приведенная ЭММ является моделью задачи целочисленного линейного программирования (ЦЛП). Для удобства записи сделаем замену двухиндексных переменных хij, и Z на одноиндексные переменные уj так как это показано в таблице раскроя (Z = y8). С учетом этих обозначений ЭММ задачи для записи ее в рабочей таблице ППП Excel будет иметь вид:
max (0y1 + 0y2 + 0y3 + 0y4 + 0y5 + 0y6 + 0y7 + 1y8)
при ограничениях:
1y1 + 1y2 + 1y3 + 1y4 + 0y5 + 0y6 + 0y7 + 0y8 = 300
0y1 + 0y2 + 0y3 + 0y4 + 1y5 + 1y6 + 1y7 + 1y8 = 500
3y1 + 2y2 + 1y3 + 0y4 + 2y5 + 1y6 + 0y7 - 2y8 ≥ 0
0y1 + 1y2 + 2y3 + 3y4 + 0y5 + 1y6 + 2y7 - 3y8 ≥ 0
yj, j = 1, 8 — целые неотрицательные.
Основные этапы компьютерной реализации этой модели представлены на рис. 2.6.
Начальная рабочая таблица и диалоговое окно Поиск решения совмещены и находятся в верхней части рисунка, результаты решения приведены в табличном виде (Отчет по результатам не приводится).
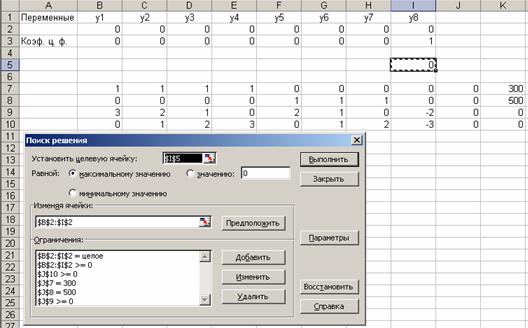
РЕЗУЛЬТАТЫ РЕШЕНИЯ
| Переменные | y1 | y2 | y3 | y4 | y5 | y6 | y7 | y8 | ||
| 0 | 0 | 0 | 300 | 380 | 0 | 120 | 380 | |||
| Коэф.ц.ф. | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | ||
| 380 | ||||||||||
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 300 | 300 | |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 500 | 500 | |
| 3 | 2 | 1 | 0 | 2 | 1 | 0 | -2 | 0 | 0 | |
| 0 | 1 | 2 | 3 | 0 | 1 | 2 | -3 | 0 | 0 |
Рис. 2.6. Основные этапы решения задачи о раскрое материалов средствами Excel
Ниже в таблице приведены указания на ячейки-формулы.
ФОРМУЛЫ РАБОЧЕЙ ТАБЛИЦЫ
| Ячейка | Формула |
|---|---|
| J5 | =СУММПРОИЗ(В2:12,В3:I3) |
| J7 | =СУММПРОИЗ(В2:12,В7:I7) |
| J8 | =СУММПРОИЗ(В2:12,В8:I8) |
| J9 | =СУММПРОИЗ(В2:12,В9:I9) |
| J10 | =СУММПРОИЗ(В2:12,В10:I10) |
Таким образом, реализуя приведенную модель средствами ППП Excel (см. рис. 2.6), получим решение:
y4 = x14 = 300; y5 = x21 = 380; у7 = х23 =120; у8 = Z= 380
(оптимальные значения остальных переменных равны нулю).
Следовательно, в данной хозяйственной ситуации максимальное количество ассортиментных наборов, равное 380 шт. можно изготовить и реализовать, если:
- раскроить каждый из 300 брусьев длиной 7,5 м на 3 детали по 2 м;
- раскроить каждый из 380 брусьев длиной 5,0 м на 2 детали по 2,5 м;
- раскроить каждый из 120 брусьев длиной 5,0 м на 2 детали по 2,0 м.
В этом случае мы получим максимальную выручку для целей погашения кредита (займа).
Пример 5. Задача оптимального формирования портфеля ценных бумаг [17]. Необходимо сформировать оптимальный портфель Марковица (минимального риска) трех ценных бумаг с эффективностями и рисками: (4, 10), (10, 40), (40, 80). Нижняя граница доходности портфеля задана равной 15.
Экономико-математическая модель
Введем необходимые обозначения, пусть хj (j = 1, 2, 3) - число предметов j-го типа, которое следует погрузить на баржу. Тогда математическая модель задачи о подборе для баржи допустимого груза максимальной ценности запишется следующим образом (см. пункт 2.1, 2,1):
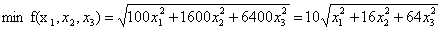
4x1 + 10x2 + 40х3 ≥ 15
x1 + x2 + x3 = 1
xj ≥ 0, j = 1, 2, 3.
Решение. Приведенная ЭММ является моделью задачи нелинейного программирования. Специальный (рабочий) лист может быть подготовлен в виде, представленном на рис. 2.7, формулы этого листа приведены в ячейках.

Рис. 2.7. Рабочий лист
Диалоговое окно, отвечающее приведенному выше рабочему листу, представлено на рис. 2.8.
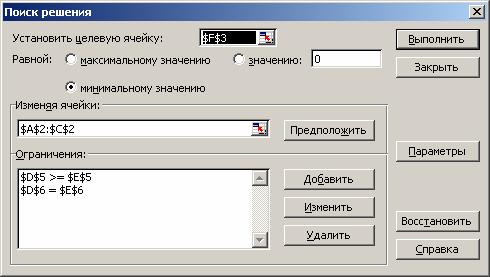
Рис. 2.8. Диалоговое окно
Реализуя приведенную модель средствами ППП Excel (рис. 2.9), будем иметь оптимальный портфель Марковица:
x1 = 0,5213, х2 = 0,2078, х3 = 0,2709,
т.е. доли ценных бумаг оказались равными 52,13 %; 20,78 % и 27,09 %. При этом минимальный риск - 23,79, доходность портфеля оказалась равной заданной - 15.
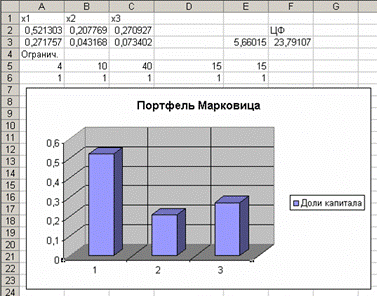
Рис. 2.9. Результаты решения
При решении приведенных выше типовых задач сознательно использовались разнообразные подходы к оформлению рабочей таблицы Excel и результатов решения. В каждой конкретной ситуации студенты вольны выбрать свой подход — с позиций содержательности, наглядности, удобства, дизайна. Результаты могут быть дополнительно представлены Отчетом по результатам или его фрагментом, кроме того, достаточно часто их целесообразно сопровождать графической иллюстрацией с помощью Мастера диаграмм (как это сделано в примере 5).
3. Задачи для самостоятельной работы и самопроверки
Составьте модель и получите решение следующих задач о смесях.
3.1. Постановка задачи. Стандартом предусмотрено, что октановое число автомобильного бензина А-76 должно быть не ниже 76, а содержание серы в нем — не более 0,3%. Для изготовления такого бензина на заводе используется смесь из четырех компонентов. Данные о ресурсах смешиваемых компонентов, их себестоимости и их октановом числе, а также о содержании серы приведены в таблице.
| Характеристика | Компонент автомобильного бензина | |||
|---|---|---|---|---|
| № 1 | № 2 | № 3 | № 4 | |
| Октановое число | 68 | 72 | 80 | 90 |
| Содержание серы, % | 0,35 | 0,35 | 0,3 | 0,2 |
| Ресурсы, т | 700 | 600 | 500 | 300 |
| Себестоимость, ден.ед./т | 40 | 45 | 60 | 90 |
Определите, сколько тонн каждого компонента следует использовать для получения 1000 т автомобильного бензина А-76, чтобы его себестоимость была минимальной.
Ответ: оптимальное решение (поведение) в данной ситуации определяется вектором объемов смешиваемых компонент (571,429 т; 0; 142,857 т; 285,714 т), оценка затрат - 57142,86 ден.ед.
3.2. Получите решение задачи о смесях (3.1), если себестоимость смешиваемых компонент составит соответственно 40, 45, 60 и 70 ден.ед./т. Все остальные характеристики и числовые данные неизменны.
Ответ: оптимальное решение (поведение) в данной ситуации определяется вектором объемов смешиваемых компонент (550 т; 50 т; 100 т; 300 т), оценка затрат - 51250,0 ден.ед.
3.3. Получите решение задачи о смесях (3.1), если себестоимость смешиваемых компонент составит соответственно 40, 35, 60 и 90 ден.ед./т. Все остальные характеристики и числовые данные неизменны.
Ответ: оптимальное решение (поведение) в данной ситуации определяется вектором объемов смешиваемых компонент (0; 600 т; 100 т; 300 т), оценка затрат - 54000,0 ден.ед.
3.4. Получите решение задачи о смесях (3.1), если себестоимость смешиваемых компонент составит соответственно 40, 35, 60 и 55 ден.ед./т. Все остальные характеристики и числовые данные неизменны.
Ответ: оптимальное решение (поведение) в данной ситуации определяется вектором объемов смешиваемых компонент (0; 600 т; 100 т; 300 т), оценка затрат - 43500,0 ден.ед.
3.5. Получите решение задачи о смесях (3.1), если себестоимость смешиваемых компонент составит соответственно 40, 35, 50 и 90 ден.ед./т. Все остальные характеристики и числовые данные неизменны.
Ответ: оптимальное решение (поведение) в данной ситуации определяется вектором объемов смешиваемых компонент (0; 333,333 т; 500 т; 166,667 т), оценка затрат - 51666,67 ден.ед.
Составьте модель и получите решение следующих задач о ранце.
3.6-3.10. Постановка задачи. Организация арендует баржу грузоподъемностью В. На этой барже предполагается перевозить груз n типов. Вес и стоимость единицы груза соответственно равны p1, р2, ..., рn и c1, с2, ..., сn. Необходимо погрузить на баржу груз максимальной стоимости.
Числовые данные для задач 3.6-3.10 представлены в таблице (в усл. ед. измер.):
| Номер задачи | p1 | p2 | p3 | p4 | p5 | В | c1 | c2 | c3 | c4 | c5 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 3.6 | 21 | 19 | 16 | 14 | 7 | 94 | 40 | 35 | 20 | 17 | 12 |
| 3.7 | 20 | 15 | 20 | 14 | - | 200 | 100 | 80 | 40 | 30 | - |
| 3.8 | 23 | 18 | 13 | 6 | 3 | 60 | 100 | 90 | 75 | 26 | 15 |
| 3.9 | 150 | 93 | 80 | 40 | - | 700 | 70 | 62 | 30 | 15 | - |
| 3.10 | 75 | 50 | 41 | 30 | - | 405 | 135 | 130 | 128 | 105 | - |
Ответ: оптимальное решение определяется вектором, компоненты которого задают количество предметов соответствующего типа, которое следует погрузить на баржу.
Задача 3.6. Оптимальное решение — 2, 2, 0, 0, 2, максимальная стоимость груза - 174 у.е.
Задача 3.7. Оптимальное решение - 1, 12, 0, 0, максимальная стоимость груза - 1060 у.е.
Задача 3.8. Оптимальное решение - 0, 0, 3, 0, 7, максимальная стоимость груза - 330 у.е.
Задача 3.9. Оптимальное решение - 0, 7, 0, 1, максимальная стоимость груза - 449 у.е.
Задача 3.10. Оптимальное решение - 0, 0, 1, 12, максимальная стоимость груза - 1388 у.е.
Составьте модель и получите решение следующих задач об инвестициях.
3.11-3.15. Постановка задачи. Предлагается n инвестиционных проектов, тщательная экономическая экспертиза которых позволяет получить для каждого из проектов достаточно убедительные экономические оценки ожидаемого эффекта от их реализации c1, с2, ..., сn и необходимых капиталовложений p1, р2, ..., рn. Общий объем возможных инвестиций ограничен величиной В. Необходимо так распорядиться имеющимися финансовыми ресурсами, чтобы максимизировать суммарный эффект от инвестиций.
Числовые данные для задач 3.11—3.15 представлены в таблице (в усл.ед. измер.):
| Номер задачи | p1 | p2 | p3 | p4 | p5 | В | c1 | c2 | c3 | c4 | c5 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 3.11 | 110 | 60 | 80 | 15 | 30 | 200 | 80 | 50 | 75 | 40 | 45 |
| 3.12 | 90 | 60 | 80 | 15 | 30 | 200 | 80 | 50 | 75 | 40 | 45 |
| 3.13 | 23 | 18 | 13 | 6 | 3 | 60 | 100 | 90 | 75 | 26 | 15 |
| 3.14 | 85 | 70 | 80 | 35 | 30 | 190 | 80 | 50 | 75 | 40 | 45 |
| 3.15 | 60 | 70 | 80 | 35 | 30 | 190 | 55 | 40 | 75 | 40 | 45 |
Ответ: оптимальное решение определяется вектором, компоненты которого задаются булевыми переменными: 1 или 0 (1-соответствующий проект следует финансировать, 0 — не следует).
Задача 3.11. Оптимальное решение - 0, 1, 1, 1, 1, максимальный эффект - 210 у. е.
Задача 3.12. Оптимальное решение - 1, 1, 0, 1, 1, максимальный эффект - 215 у.е.
Задача 3.13. Оптимальное решение - 1, 1, 1, 0, 1, максимальный эффект - 280 у.е.
Задача 3.14. Оптимальное решение - 1, 1, 0, 0, 1, максимальный эффект - 175 у.е.
Задача 3.15. Оптимальное решение — 1, 0, 1, 0, 1, максимальная эффект - 175 у.е.
Составьте модель и получите решение следующих задач об оптимальном распределении выпуска продукции по технологиям производства.
3.16-3.20. Постановка задачи. Предприятие располагает двумя способами производства данного вида продукции. В течение рассматриваемого периода времени необходимый объем продукции равен В = Х1 + Х2, где Х1 и Х2 — объемы производства по соответствующему технологическому способу. Затраты производства S при каждом способе зависят от объемов нелинейно:
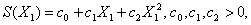
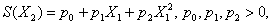
Необходимо так распределить объем производства между технологическими способами, чтобы минимизировать общие затраты производства.
Числовые данные для задач 3.16-3.20 представлены в таблице (в условных ед. измерения):
| Номер задачи | p0 | p1 | p2 | В | c0 | c1 | c2 |
|---|---|---|---|---|---|---|---|
| 3.16 | 5 | 1 | 2 | 100 | 3 | 2 | 1 |
| 3.17 | 5 | 1 | 2 | 100 | 3 | 2 | 3 |
| 3.18 | 5 | 1 | 1 | 100 | 3 | 2 | 1 |
| 3.19 | 1 | 1 | 1 | 100 | 1 | 1 | 1 |
| 3.20 | 1 | 2 | 1 | 100 | 1 | 1 | 1 |
Ответ: оптимальное решение определяется вектором, компоненты которого задают объемы выпуска продукции по технологиям производства.
Задача 3.16. Оптимальное решение - 66,5; 33,5, минимальные затраты производства составят 6841,25 у.е.
Задача 3.17. Оптимальное решение - 39,9; 60,1, минимальные затраты производства составят 12147,95 у.е.
Задача 3.18. Оптимальное решение - 49,75; 50,25, минимальные затраты производства составят 5157,875 у.е.
Задача 3.19. Оптимальное решение - 50,0; 50,0, минимальные затраты производства составят 5102,0 у.е.
Задача 3.20. Оптимальное решение - 50,25; 49,75, минимальные затраты производства составят 5181,875 у.е.
Составьте модель и получите решение следующих задач о назначениях [16].
3.21. Постановка задачи. В распоряжении некоторой компании имеется 6 торговых точек и 6 продавцов. Из прошлого опыта известно, что эффективность работы продавцов в различных торговых точках неодинакова. Коммерческий директор компании произвел оценку деятельности каждого продавца в каждой торговой точке. Результаты этой оценки представлены в таблице.
| Продавец | Объем продаж по торговым точкам, USD/тыс. шт. | |||||
|---|---|---|---|---|---|---|
| I | II | III | IV | V | VI | |
| А | 68 | 72 | 75 | 83 | 75 | 69 |
| В | 56 | 60 | 58 | 63 | 61 | 59 |
| С | 35 | 38 | 40 | 45 | 25 | 27 |
| D | 40 | 42 | 47 | 45 | 53 | 36 |
| Е | 62 | 70 | 68 | 67 | 69 | 70 |
| F | 65 | 63 | 69 | 70 | 72 | 68 |
Как коммерческий директор должен осуществить назначение продавцов по торговым точкам, чтобы достичь максимального объема продаж?
Ответ: Оптимальное решение определяется матрицей назначений Х = (xij), результаты решения содержатся в следующей таблице
| X = | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 1 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | ||
| ЦФ = 371 долл. | |||||||
3.22. Решите задачу 3.21 при условии, что назначение х14 недопустимо, т.е. вместо элемента 83 в матрице объемов продаж можно принять, например, число (-100).
Ответ: Оптимальное решение определяется матрицей назначений Х = (xij), результаты решения содержатся в следующей таблице
| X = | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 1 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | ||
| ЦФ = 368 долл. | |||||||
3.23. Решите задачу 3.21 при условии, что имеется только 5 продавцов, т.е. шестая строка в матрице объемов продаж отсутствует.
Ответ: оптимальное решение определяется матрицей назначений Х = (xij), результаты решения содержатся в следующей таблице
| X = | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 1 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | ||
| ЦФ = 306 долл. | |||||||