В начало

Литература

Приложение 3. МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ

Матрицей называется прямоугольная таблица чисел. Например:

,

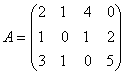Y = (1 2 3),

.

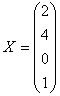Число строк и столбцов матрицы определяют ее размерность. Если матрица состоит из 3 строк и 4 столбцов, ее размерность - 3×4; в общем случае m строк и n столбцов размерность равна m×n.Таблица, состоящая из одной строки или одного столбца, называется вектором-строкой или вектором-столбцом соответственно.

Общий элемент матрицы А записывается как а_ij

.

Здесь, например, а₁₁ = 2, а₁₂ = 1, и т.д. Первый индекс - это номер строки, второй - номер столбца. Общие элементы векторов записывают с одним индексом: x_j, y_i, так что

,

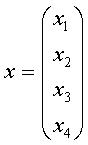y = (y₁, y₂, y₃).

При выполнении определенных условий с матрицами и векторами можно оперировать также как с числами.

Равенство матриц и векторов

Матрицы А и В равны, если

a_ij = b_ij

для всех i, j.

Ясно, что сравнивать можно только матрицы с одинаковым числом строк и столбцов (одинаковой размерности). Если это условие не выполнено, матрицы не сравнимы. Например, вектора

(1 2 3)

и

не равны, хотя все их элементы с одинаковыми индексами равны.

Транспонирование матриц и векторов

Матрица В называется транспонированной к матрице А:

В = А^Т,

если

b_ij = a_ij

т. е. если столбцы и строки поменялись местами. Например:

,

,

.

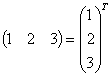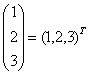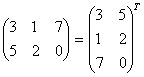Сумма и разность матриц и векторов

Пусть матрицы А и В имеют одинаковый порядок, т. е. число строк матрицы А равно числу строк матрицы В и число столбцов матрицы А равно числу столбцов матрицы В. Матрицы С и D - сумма и разность матриц А и В:

С = А + В,

D = А - В,

если

c_ij = a_ij + b_ij,

d_ij = a_ij - b_ij,

Например:

,

.

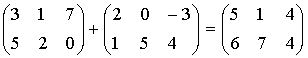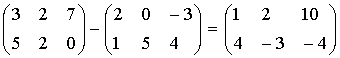Умножение скаляра (числа) на матрицу

В = λ * А,

где λ - скаляр (число). В индексной записи:

b_ij = λ * а_ij.

Например:

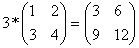
Умножение матрицы на скаляр не определено, т. е. выражение

С = А * λ

не имеет смысла.

Скалярное произведение векторов

Пусть х - вектор-строка, а у - вектор-столбец одинакового порядка п. Скалярным произведением векторов х и у называется выражение

.

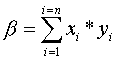Например:

.

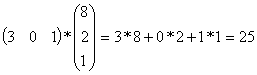Умножение матриц

Пусть матрица А имеет k строк и m столбцов, матрица В имеет m строк и n столбцов. Существует матрица С, являющаяся произведением матриц А и В:

С = А * В,

такая, что

.

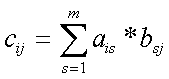Например:

,

.

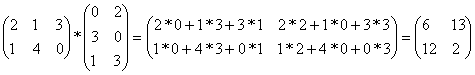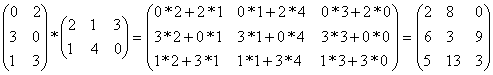В правиле умножения матриц нет ничего сложного. Элемент результирующей матрицы в строке i и столбце j равен скалярному произведению i-й строки левого сомножителя на j-й столбец правого сомножителя:

.

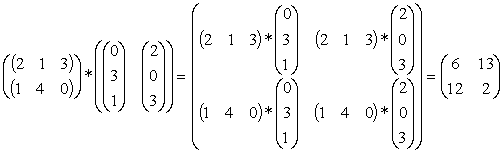Все, что надо запомнить, - это то, что СЛЕВА ВСЕГДА СТРОКИ, СПРАВА - ВСЕГДА СТОЛБЦЫ. Индексы, указывающие, в какой строке и в каком столбце расположен элемент матрицы, записываются в том же порядке: сначала номер строки, потом номер столбца; левый сомножитель в произведении матриц состоит из строк, правый - из столбцов. Как видно из приведенных выше примеров, от перемены мест сомножителей результат может измениться: произведение матриц не коммутативно. Особенно наглядно это свойство матричного произведения проявляется в следующем примере:

,

.
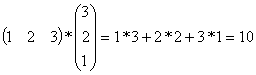
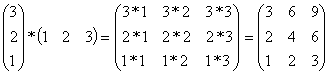