В начало

Список литературы

Глава 5. ПЯТОЕ ИЗМЕРЕНИЕ

«Знаете ли вы, что на самом деле мы вовсе не трехмерные существа? Что мы не ограничены во времени и пространстве? Что время — это лишь иллюзия? Что окружающая нас реальность — совершенно не то, чем она кажется, что она может оказаться лишь коллективной проекцией человеческого духа?

В этой главе мы попробуем совершить небольшую экскурсию в мир измерений и посмотреть, как компьютер может помочь нам открыть совершенно новые миры, увидеть самих себя и окружающий мир в совершенно новом свете. Мы побываем в двух- и трехмерных мирах, исследуем время и пространство, а затем совершим бросок в четвертое измерение, которое действительно стало доступным благодаря компьютерной программе. Вы научитесь видеть вещи в четырех измерениях и откроете для себя невероятно интересные сферы жизни, которые послужат важным импульсом для вашего духовного развития.

Попробуем продемонстрировать всю иллюзорность наших представлений о так называемой реальности. Вся эта привычная для нас система конструируется единственно и исключительно в нашем мозгу. Мы увидим, какие поразительные эффекты могут возникнуть, если — пусть даже лишь мысленно — переместиться в миры, где вместо трех существуют всего два или целых четыре, а то и пять измерений. Еще до великого греческого философа Платона человечество задумывалось о природе реальности, и ученые компьютерного века используют весь мощный потенциал суперкомпьютеров, чтобы разгадать загадку измерений Вселенной.

Задавались ли вы хотя бы однажды вопросом о том, что представляет собой «реальный мир»? Реальный мир, или, вернее, то, что мы под этим подразумеваем, — это живые существа и объекты, которые мы можем реально воспринимать. Нас окружают материальные объекты, люди, животные, растения, минералы и созданные человеком предметы. Мы считаем объект реальным, если можем не только увидеть его, но и потрогать, если его параметры можно измерить с помощью различных приборов и если его свойства подчиняются всеобщим физическим законам. Реально и объективно то, что существует независимо от нас, а субъективно или вымышлено то, что существует лишь в виде некой идеи в нашем сознании. Такой предстает картина мира для большинства современных людей.

Приходилось ли вам когда-нибудь бывать на выставке голограмм? Если да, то вы видели там объекты, которые как будто парят в пространстве. Можно даже обойти эти экспонаты и рассмотреть их со всех сторон. Парящее в пространстве голографическое яблоко кажется вполне реальным и действительно существующим. Оно действительно реально — или перед нами лишь плод воображения? Если его нет в действительности, то что же это тогда? Ловко сфабрикованная проекция? Но что если так называемое реальное яблоко — тоже только проекция, пусть более детальная и доступная остальным нашим органам чувств?

О природе реальности в наши дни больше всех размышляют физики. Вопросы об истинной сути вещей издавна занимали философов — как на Востоке, так и в Европе. В зависимости от того, к какой школе они принадлежали, выводы из их размышлений оказывались весьма различными. Но применимыми на практике и поддающимися проверке были и остаются, собственно говоря, лишь утверждения индийских философов. Древнеиндийские школы отличаются тем, что помимо занятий чисто теоретической философией они также используют практические духовные методы, позволяющие их приверженцам почувствовать, какие из теоретических утверждений справедливы, а какие нет.

При этом индийцы исходят из того, что по мере накопления духовного опыта в конечном счете все должно поддаваться проверке. На Западе, напротив, преобладает мнение, что любую теорию надо проверить с помощью научных экспериментов в так называемом внешнем мире.

Для духовного развития полезно попробовать отказаться от привычной картины трехмерной материальной Вселенной. Чтобы добиться этого, нужно понять истинную суть внешнего мира. Как ни удивительно, в этом может помочь компьютер. Как именно, вы узнаете чуть позже.

Что же такое внешний мир и что скрывается за понятием трехмерности? Наши чувства приносят нам информацию о мире, который кажется трехмерным. Если в этот момент вы сидите в обычной комнате, то в каждом углу увидите то, что математики называют системой координат: систему из трех взаимно перпендикулярных линий, образованную тремя гранями — двумя стенами и потолком (или полом). Вы можете назвать эти линии длиной, шириной и высотой. Положение любой точки в комнате можно описать, если из определенного выбранного угла (начала системы координат) отмерить нужное расстояние параллельно одной из стен, затем — другой отрезок параллельно другой стене и третий отрезок — в высоту.

Таким образом, понятие «трехмерный мир» означает, что, задав три параметра, можно однозначно определить местонахождение любой точки в пространстве. В приведенном примере эти параметры можно назвать просто длиной, шириной и высотой. Теоретически можно представить себе двухмерный мир, где будут только длина и ширина. В таком мире все вокруг нас было бы плоским. Одномерный мир — это мир линии, в нем определена одна только длина. В дальнейшем мы увидим, что линейный и плоский миры могут помочь нам представить, что такое четырех- или пятимерный мир.

Положение предмета в пространстве можно определить с помощью не только длины, ширины и высоты, но и совершенно других параметров. Но для трехмерного мира важно, что таких параметров всегда будет три. Зная три правильно выбранных параметра или координаты, можно отыскать в этом мире любую точку. Возьмем географическое положение какой-нибудь точки на планете. Для этого по традиции нулевую точку системы координат помещают в центр Земли. Любая точка на планете удалена от этого центра на одно и то же расстояние, а именно — на 6300 км. Таким образом, первый параметр — удаленность от нулевой точки — для всей земной поверхности одинаков. Исключение составляют лишь самые высокие горы — на 8 км дальше — и самые глубокие впадины — на 10 км ближе. Но по сравнению с радиусом Земли эта разница довольно незначительна. Второй и третий из необходимых параметров — это угловые координаты, которые известны нам как географические широта и долгота. Итак, с помощью трех параметров можно однозначно определить положение любой точки в трехмерном пространстве — в данном случае любой точки на поверхности Земли.

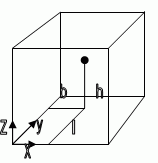
Рис. 1. Система координат и определение положения точки в трехмерном пространстве

Однако в упорядоченном пространстве трехмерного мира встречаются феномены, которые не вписываются в эту схему. Прочитав данную главу, вы, возможно, посмотрите на мир совершенно другими глазами, и в этом вам поможет компьютер. Давайте обратимся к природе объекта, который мы воспринимаем как реально существующий в этом трехмерном мире. Для начала попробуем осознать самое поразительное: мы вообще не знаем, что такое реальный объект, как не знаем и того, реальна ли картинка на экране монитора. Как это получается?

Как мы воспринимаем объекты внешнего мира?

Образ объекта внешнего мира вначале появляется в нашем мозгу под воздействием сигналов, полученных от органов чувств. Управляющие ими нервные центры можно уподобить адресатам, которые получают сигналы одновременно по пяти каналам. Из этой информации, исходящей от органов чувств, конструируется внутренний образ объекта.

Возьмем в качестве примера зрение. Сегодня мы знаем, что видимый нами свет — это электромагнитные колебания различной частоты, которые, однако, составляют лишь незначительную часть всего спектра электромагнитных колебаний. К длинноволновой части спектра, помимо прочих, относятся радио- и телевизионные волны, а также волны, используемые для сотовой связи. В коротковолновой части, к примеру, находятся гамма- и рентгеновское излучения. Отраженный от объекта или излучаемый свет — это единственные колебания, которые мы воспринимаем, и, таким образом, они передают нам лишь часть информации об объекте — ведь любой объект отражает огромный спектр волн, а не только видимый нами свет. Остальные органы чувств также доносят до нас лишь часть сведений об окружающем. Следовательно, возникающая в нашем мозгу картина объекта — это лишь его отдаленное подобие, составленное с использованием минимума информации. Оно совершенно не передает его настоящего, полного образа.

И если, зная все это, тем не менее считаем возникающий у нас внутренний образ относительно правильным, мы заблуждаемся. Мы проецируем внутренний образ вовне автоматически, потому что «знаем», что объект существует вне нас, а не в нашем мозгу. Собственно говоря, мы движемся во внутреннем мире, составленном из подобий внешних объектов, которые вновь спроецированы вовне, в так называемый объективный мир: мы просто-напросто придумываем тот мир, который находится снаружи!

В довершение этой путаницы мы проецируем трехмерный образ в трехмерное пространство, хотя природа объекта вовсе не связана с тремя измерениями. Это объясняют тем, что наш ум якобы не может осмыслить больше трех измерений. Но для математики — той дисциплины, с помощью которой мы можем записать на языке формул все естественные законы, — не составляет никакого труда оперировать более чем тремя измерениями. Точно так же многомерные миры доступны компьютеру. Многомерное пространство, например, с четырьмя, пятью или тридцатью измерениями — совершенно нормальное явление для математики, но не для нашего сознания! Сознание создает трехмерный мир, потому что так устроены нервная система и функции мозга, но не потому, что мир на самом деле трехмерный.

Следовательно, не объекты трехмерны, а наш мозг работает таким образом, что предоставляет нам трехмерную картину мира. Не только в математике не составляет труда оперировать многомерными пространствами — в физике тоже сегодня требуется больше измерений, чем привычные для нашего мышления три. Физики говорят о «нулевой энергии», об «энергии вакуума», о «криволинейном пространстве» и «гиперпространстве». С начала XX столетия ученые — такие как Альберт Эйнштейн или Макс Планк — основательно изменили наши представления о пространстве.

«Яблочные человечки» Мандельброта

С помощью компьютера математики XX столетия смогли также показать, что с привлечением измерений, которые не воспринимаются нашими органами чувств, но могут быть рассчитаны математически, возникают просто поразительные миры и пространства. Фракталы математика Бенуа Мандельброта¹, самый знаменитый из которых называется «яблочный человечек», совершили триумфальное шествие по миру. Путем математических операций с введением так называемых мнимых чисел ему удалось создать на экране компьютера фантастически необычные и завораживающие картины, которые часто представляют собой как бы дробящееся до бесконечности изображение.

Эти фракталы созданы на основе простых математических формул. Особенность их заключается в том, что при увеличении какой-то одной заинтересовавшей вас области готового фрактала в увеличенной детали повторяется общая структура всего объекта, то есть в маленьком фрагменте «яблочного человечка» вновь виден «яблочный человечек», и т. д.

Рис. 2. «Яблочный человечек» Бенуа Мандельброта

Это может повторяться до бесконечности, будто мы погружаемся в мир внутри некоего мира, который, в свою очередь, находится внутри другого мира... Здесь мы не будем более подробно обсуждать фракталы или связанную с ними теорию хаоса. По этому вопросу существует обширная литература и есть программы, позволяющие самостоятельно установить фракталы на своем компьютере.

Что такое четвертое измерение и какое отношение к нему имеет йога?

При попытке описать или хотя бы просто понять четвертое или пятое измерение, которые обычный человек не может себе представить, мнения разделяются. Ниже приведены программы, которые могут воспроизвести эти измерения на вашем компьютере. Некоторые теоретики пытаются описать четвертое измерение как пространственное, другие считают, что это время. Некоторые рассматривают четвертое и пятое измерения как временные, другие же в качестве пятого измерения рассматривают позицию наблюдателя, с которой можно видеть оставшиеся четыре измерения. Но почему так важно понять, что именно представляют собой предполагаемые следующие измерения?

Естествознание неизбежно должно ставить перед собой такую задачу, поскольку оно претендует на то, чтобы объяснить все явления природы. Однако, используя трехмерную модель, оно не в состоянии этого сделать. В квантовой физике, например, влияние наблюдателя эксперимента само по себе является решающим фактором при построении модели. Кроме того, физика во многих своих формулах уже принимает во внимание время, при этом не считая его четвертым измерением, однако она вообще не объясняет, что такое время. Мы и по сей день не знаем, что оно собой представляет, хотя постоянно имеем с ним дело, или, лучше сказать, в реальной жизни нам постоянно приходится с ним сталкиваться.

Для тех, кто занимается духовным развитием, феномен времени неизбежно должен играть важную роль в росте самосознания и в понимании мнимой природы всех внешних объектов и событий. Как однажды заметил известный йог Парамахамса Иогананда², все, что мы привыкли видеть вокруг, подобно игре теней на киноэкране, то есть лишено всякой сущности. Осознав, что киноэкран — это символическое представление нашего сознания, можно очнуться от коллективного сна, в который погружена большая часть человечества. В древнеиндийских трактатах, например, йога-сутрах Патанджали, самым подробным образом проанализирована природа духа, времени и внешних объектов нашего мира, который кажется трехмерным. В древних текстах точно описано, как можно представить состояния внешнего объекта, следующие во времени друг за другом, как они связаны с работой нашего ума.

Окно во времени Дж. У. Дьюнна

Оставив индийских йогов и обратившись к западным мыслителям, мы также находим немало любопытного. Например, это фантастические работы Дж. У. Дьюнна, написанные в начале XX века и касающиеся природы времени. Его рассуждения поразительны. Проводя опыты с группами студентов Оксфордского университета, Дьюнн установил, что наше понимание времени до сих пор остается весьма ограниченным. У нас не хватает опыта и знаний, чтобы постичь истинную природу времени. Путем многочисленных экспериментов ученый доказал, что во сне мы можем заглянуть как в прошлое, которое обычно называем воспоминаниями, так и в будущее!

Исходя из этого, он создал свою теорию времени. В ее основе лежит гипотеза о том, что помимо трех пространственных мы движемся также во множестве временных измерений. На основе своих опытов Дьюнн предположил, что обычно нам доступно лишь весьма узкое «окно восприятия», которое движется в четырехмерном пространстве, при этом четвертым измерением считается время. Окно — это «настоящий момент». Оно представляет собой лишь небольшой фрагмент окружающего нас мира. Более или менее постоянное движение этого окна восприятия позволяет нам воспринимать мир как последовательность событий, череду следующих друг за другом явлений. Возникает «естественный» ход событий — причинно-следственная цепочка. Но во сне кажется, будто узкое окно восприятия, открытое нам в бодрствующем состоянии, расширилось и мы можем одновременно взглянуть как в прошлое, так и в будущее. Дьюнн подтверждает это своими экспериментами.

Правда, впоследствии Дьюнн запутался во все возраставшем количестве временных измерений. Он считал, что наше окно восприятия имеет определенную скорость и движется во времени, которое, однако, служит измерением в следующем пространстве, то есть не является тем, что мы привыкли называть временем. Таким образом, перед Дьюнном встала необходимость ввести пятое измерение. Хотя его размышления весьма увлекательны и блестяще разработаны, их всё же не стоило доказывать столь сложным образом. Дьюнн просто упустил из виду, что внутренний наблюдатель, который может зафиксировать движущееся окно восприятия, вовсе не обязательно будет связан с другим временем из последующего, пятого измерения, а может быть вообще независим от времени! Правда, эта идея предполагает знание о том, что не всё в нас, людях, связано с пространством и временем, о том, что мы — многомерные существа и лишь частью своей психики и телом воспринимаем окружающий мир как трехмерный.

В многочисленных древнеиндийских и тибетских рукописях мы находим четкие указания на то, что истинная природа человеческого духа хотя и познаваема, но не связана со временем.

В этих старинных культурах сосуществовали различные философские школы, которые были единодушны в одном: человек с помощью длительных упражнений способен познать истинную природу своего духа. Обратив взгляд внутрь себя, можно увидеть не только внутреннего наблюдателя, который существует вне пространства и времени, но и нашу собственную духовную сущность, наше действительное, или божественное, «я», чей дом - вечность. Пространство и время, напротив, лишь изменчивые объекты познания. При этом сам наблюдающий дух неизменен и не зависит от времени.

«Внутренняя природа духа неопределима и не представима, однако она вечна и неизменна»³.

«Наблюдатель и первично узнающий — его сущности, которые распространяются на время и пространство. Время и пространство — это формы знания; поэтому сущность того, кто понимает это, лежит вне пространства и времени»⁴.

Условный наблюдатель, в понимании Дьюнна, должен находиться в ином временном измерении, не в том, где мы обычно находимся в состоянии бодрствования, и, следовательно, должен быть отделен от нашего трехмерного мира. Итак, что же такое четвертое и пятое измерения, если это не время?

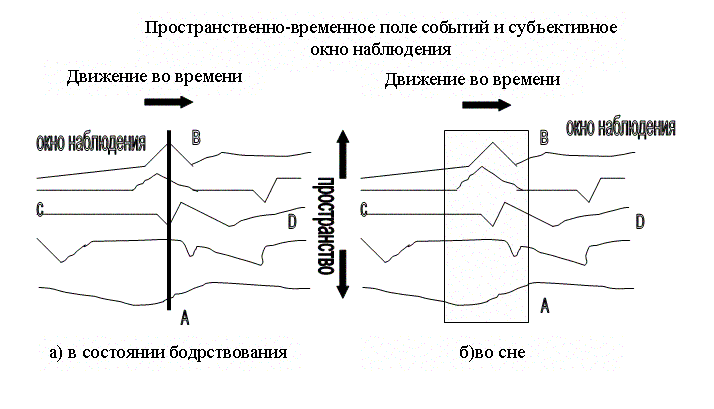
Рис. 3. Расширение окна восприятия во сне

Время и четвертое измерение в физике

Из физиков нового времени в этой связи следует упомянуть русского ученого Николая Козырева, чьи книги, к сожалению, большей частью не переведены на немецкий. Описание его теорий можно найти в книге «На пути к пониманию феномена времени» (On the Way to Understanding the Time Phenomenon)⁵ американского издателя Э.П. Левича. Козырев пишет о физически существующем временном потоке. Он развивает теорию, согласно которой живая система использует этот временной поток как свободно доступную энергию. Подобным образом неподвижные звезды преобразуют энергию потока времени, который теснейшим образом связан с гравитацией, в световое излучение. Таким образом, звезды – это вовсе некосмические ядерные реакторы, излучающие выделяемую энергию в виде света и тепла. Вернее будет представить их трансформаторами энергии гравитации и времени. Согласно теории Козырева, мы также трансформируем энергию времени в солнечной системе в жизненную энергию.

Все эти рассуждения свидетельствуют о том, что мы и по сей день не понимаем, как различные энергетические поля, открытые физиками к настоящему моменту, соотносятся друг с другом и какое отношение они имеют к последующим измерениям. Еще в XIX веке британский физик Джеймс Клерк Максвелл открыл формулы, описывающие все эти взаимосвязи. Однако в том виде, в каком он их преподнес, в то время они казались непонятными. Знаменитые уравнения Максвелла, которые сегодня известны любому физику или инженеру по электротехнике, были искажены. Между тем некоторые авторы утверждают, что Альберт Эйнштейн, хотя и создал так долго искомую единую теорию поля, объясняющую, в частности, феномен поля и последующих измерений, однако был вынужден передать результаты своих работ американским военным⁶.

Итак, феномен времени можно изучать как с субъективной точки зрения, так и с позиций объективной науки. Необъяснимые скачки во времени, которые наблюдаются снова и снова и подтверждены документально, тоже когда-нибудь найдут свое объяснение. Даже существование знаменитой машины времени, описанной Г. Уэллсом в одноименном романе, становится, таким образом, все более возможным. Поскольку путешествия во времени всегда были весьма привлекательной темой, одному из событий такого рода, действительно произошедшему в Англии XX веке, посвящена последняя глава этой книги (см. главу 13 «Прыжок во времени»).

Четвертое измерение на экране монитора

Все попытки человека осмыслить время как еще одно измерение показывают, насколько ограничены возможности нашего разума. Нам невероятно трудно выйти за рамки третьего измерения. Некоторые ученые и любители науки считают, что четвертое измерение, как и три предыдущих, является пространственным, а не временным. Однако мы все равно не можем его себе представить. Результаты изысканий, полученные приверженцами этой теории, можно продемонстрировать на компьютере. Соответствующие программы способны потрясти основы нашего восприятия.

Первую программу подобного рода, которая более двенадцати лет назад получила всемирную известность, разработал американский ученый Томас Банчофф со своими коллегами из лаборатории компьютерной графики Броуновского университета в Провиденсе (Род-Айленд, США). Некоторые пользователи говорят, что их восприятие мира изменилось благодаря одному только созерцанию движущихся графических изображений и что теперь они легче могут представить себе следующие измерения.

Прыжок в следующее измерение

Однако прежде чем погрузиться в четвертое измерение, приблизимся к нему и к его компьютерному отображению постепенно, шаг за шагом, тем путем, который описывает в своей книге «Tertium Organum» Петр Успенский, философ и ученик Георгия Ивановича Гурджиева⁷. Это позволит нам понять и использовать интересные возможности компьютерных программ, о которых мы и не подозревали. Чтобы прыжок в четвертое измерение легче было себе представить, Успенский прибегает к аналогии. Похожим образом в конце XIX веке неизвестные нам измерения в весьма юмористической форме попытался описать английский автор, преподаватель и шекспировед Эдвин Э. Эббот в своей классической «Флэтландии», или «Плоском мире»⁸. Тогда он подписался псевдонимом Э. Сквэйр (по-русски: «Квадрат»). Эта мера предосторожности связана, конечно, не с занимательным изображением вещей и существ, чей облик столь непривычен для нашего мира, а с его особым юмором. Он использовал аналогию с существами, обитающими во Флэтландии, которых он изобразил как треугольник, пятиугольник, круг и т. д., чтобы разоблачить общественные нравы викторианского плоского мира. С едкой иронией, граничившей с цинизмом, он выступил против английского общественного строя XIX столетия.

Чтобы лучше представить последующие измерения, рассмотрим еще несколько примеров наиболее просто сконструированных миров. Они объясняют, отчего так трудно заниматься четвертым и последующими измерениями. Нам предстоит понять, что мы слишком привыкли мыслить в категориях трех пространственных измерений.

Как уже было сказано, в пространстве есть длина, ширина и высота, то есть три направления, располагающихся взаимно перпендикулярно. Математик сказал бы, что в нашем пространстве вводится трехмерная система координат, оси которой взаимно перпендикулярны (см. приведенный выше пример — угол комнаты). Но если бы наш мир был двухмерным, в нем существовали бы длина и ширина, но не было бы высоты. Мы двигались бы по плоскости, не имея понятия о том, что существует «над» и «под». Если упростить наш мир еще больше, до одного-единственного измерения, он будет представлять собой просто линию, и все, что находится справа или слева от нее, мы просто не сможем воспринимать.

Приключения линейного существа

Итак, для начала представим себе одномерное существо, которое может передвигаться исключительно по прямой. Для него не существует ни правого, ни левого, ни верха, ни низа — есть только «вперед» и «назад». Такое линейное существо, опирающееся исключительно на собственное восприятие, вовсе не подозревает о возможности существования двухмерного пространства. Представим себе, что сбоку, то есть в двумерном пространстве, движется окружность, пересекая его «родную» линию. Сначала она коснется линии в одной точке, потом на линии возникнут две точки, которые сперва будут удаляться друг от друга, а затем, когда окружность перевалит за половину, вновь будут двигаться навстречу друг другу, пока не сольются в одной точке; потом окружность снова полностью исчезнет из области восприятия, доступной линейному существу. С нашей точки зрения, мы прекрасно понимаем, что происходит на самом деле. Однако одномерный наблюдатель видит лишь точки пересечения окружности и линии, которые, возникают из ниоткуда и не обнаруживают между собой никакой видимой связи.

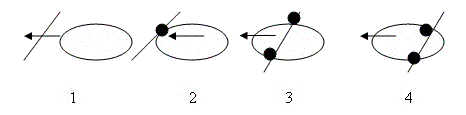
Рис. 4. Круг, который движется, пересекая одномерный линейный мир

Теперь немного изменим условие и вместо окружности рассмотрим круг, окрашенный в какой-либо цвет, допустим в красный. Тогда наш одномерный наблюдатель увидит якобы возникшую из ничего красную точку, выросшую затем в красный отрезок, который сначала будет увеличиваться, потом уменьшаться, наконец, вновь превратится в точку и совсем исчезнет. Если попробовать рассказать о происходящем, описав такую линию, изменяющую свою длину, то вообще не возникнет мысли о круге, и соответственно останется непонятным, что привело к возникновению такого феномена красной линии. Дополнительная трудность состоит в том, что линейное существо не видит линию сверху, как видим ее мы, и, чтобы составить представление о ее длине, оно должно «проехаться» по линии. Это существо не может отступить в сторону или приподняться над линией, чтобы рассмотреть феномен с другой позиции.

Вы уже догадываетесь, почему мы начали с такого простого примера, чтобы в конце концов приблизиться к четвертому измерению, недоступному для нашего восприятия? В уже упоминавшейся книге «Флэтландия» есть замечательный диалог, в котором герой этой истории, житель плоского мира с двумя измерениями, пытается объяснить монарху линейной вселенной, что такое плоскость. Попытка эта заканчивается крахом, поскольку линейный монарх остается при своем мнении, в уверенности, что вне его линии не существует больше ничего и эта линия представляет собой всю известную вселенную. Тот, кто утверждает что-то иное, просто сумасшедший, и его следует держать взаперти. Здесь Эббот, описывая судьбу рассказчика, как бы предвосхитил свою собственную участь. Заметим, что в 1600 году в Риме был сожжен на костре итальянский монах Джордано Бруно. Он был объявлен еретиком и обвинен в «теологических заблуждениях». Среди прочего он утверждал, что в бесконечной Вселенной существует бесконечно много обитаемых миров и что Земля круглая...

Чудо в стране «плоских существ»

В следующем примере представим себе двухмерное существо, которое может передвигаться по плоскости, но не имеет ни малейшего понятия о мире над этой плоскостью или под ней. Пространство для этого существа простирается в любую сторону плоскости, но лишь на ней. Теперь представим, что сверху, то есть в третьем измерении, не существующем для этого наблюдателя, опускается круглый стержень, то есть трехмерный объект, пересекающий рассматриваемую плоскость. В месте их пересечения без всяких видимых причин возникает круг, который можно наблюдать на протяжении всего времени, пока стержень будет пересекать плоскость. Затем он исчезнет так же внезапно, как и появился.

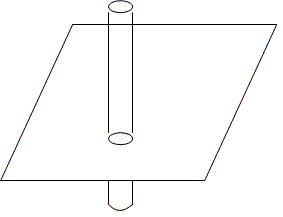
Рис. 5. Стержень движется из третьего измерения через двухмерный плоский мир

Другой похожий пример. Шар, то есть трехмерное тело, приближается к плоскости сверху. Существа плоского мира точно так же ничего не подозревают о его существовании до тех пор, пока он не коснется плоскости. В этот момент на плоскости возникает точка, которая затем превращается в круг. По мере прохождения шара сквозь плоскость этот круг сначала растет, затем уменьшается, пока вновь не становится точкой и не исчезает окончательно. Старательно наблюдая круг, который появляется на плоскости и затем исчезает, двухмерное существо все же не сможет сделать выводы о действительной причине появления и исчезновения этого круга. Ведь обитатель плоскости не может ни увидеть шар, ни воспринять его как-то иначе. Он и понятия не имеет о том, что нечто может появиться сверху и исчезнуть внизу, — верха и низа в его мире просто не существует.

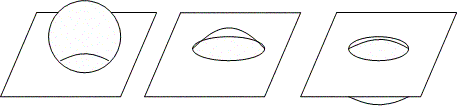
Рис. 6. Круг движется сквозь плоскость

Помимо прочего, эти примеры показывают, что наблюдатели из предыдущих измерений, опираясь на свое восприятие, и не подозревают, что в основе описанных удивительных событий, происходящих в их мире, лежит движение. Они считают, что речь идет о неком преходящем, спонтанно возникающем феномене, о появлении и исчезновении. Линия возникает и пропадает, маленькая точка превращается в круг, который все увеличивается, а потом вновь уменьшается и исчезает. Но в действительности ничего не появляется и не исчезает — просто тела, которые существовали и продолжают существовать, равномерно движутся одно сквозь другое. При этом они ничуть не меняются. Причина изменений, наблюдаемых в двухмерном мире, кроется в движении, а вовсе не в действительном изменении следующего, трехмерного мира. А что если возникновение и исчезновение в нашем мире тоже связаны не с процессами изменения, а лишь с движением неких остающихся неизменными тел сквозь четвертое измерение?

Неисследованный мир четвертого измерения

Теперь вы уже достаточно подготовлены, чтобы отважиться сделать шаг в следующее, четвертое измерение. Представим себе существо из трехмерного пространства, которое воспринимает мир так же, как люди. В это трехмерное пространство проникает какое-либо гипотетическое четырехмерное тело. Мы не знаем, как оно выглядит, но можем описать его математически. Подобно тому как в прошлом примере на плоскости при пересечении ее трехмерным шаром возникал круг, так в нашем пространстве возникает трехмерный шар, который увеличивается, затем уменьшается и исчезает.

Но как выглядит четырехмерное тело, при пересечении которого с нашим миром появляется шар? Как раз этого мы не можем представить, наш ум бессилен перед этим вопросом. Мы можем лишь рассматривать проекцию четырехмерного тела в предыдущем измерении — в нашем примере это возникающий из ничего трехмерный шар. Этот шар не дает практически никакого представления о том, как в действительности выглядит четырехмерное тело, послужившее причиной появления шара.

Развивая мысль, высказанную в предыдущей главе, можно выдвинуть следующую гипотезу: что, если изменениям, которые происходят с человеком в нашем обычном мире (он появляется на свет, растет, стареет и, наконец, умирает), в четвертом измерении соответствует лишь движение некоего остающегося неизменным четырехмерного тела? Очевидно, здесь перед нами движение во времени некоего неизменного(!) четырехмерного человека. Но каково время, в котором движется четырехмерный человек? Подобно ли оно нашему, земному, которое для нас имеет некую продолжительность? Если да, то мы сможем воспринять и четвертое измерение.

Еще одно приключение в плоском мире

Поскольку в последнем примере мы действительно подошли к границам нашего представления о мире, попробуем еще раз вернуться из третьего во второе измерение. Мы вновь рассмотрим двухмерное существо, передвигающееся на плоскости и не знающее ни верха, ни низа. Но на этот раз плоскость изогнута, однако обитатель двухмерного мира ничего об этом не знает. Для простоты представим себе лист бумаги, свернутый полукругом. Для двухмерного существа этот лист по-прежнему остается плоскостью с двумя измерениями, оно не замечает в ней никакого изгиба. Теперь будем продвигать соломинку сквозь бумагу, при этом в местах пересечения возникнут два круга (или овала). Соломинка останется невидимой, так как она принадлежит третьему измерению. Для двухмерного обитателя появятся два независимых объекта, два круга, которые, в его восприятии, не имеют друг с другом ничего общего. Возможно, ученые этой плоскости обратят внимание не только на возникновение этих кругов, но и на некоторые совпадения: каждый раз, когда возникает один круг, в другом месте появляется также и второй. Некоторое время оба эти круга существуют одновременно, и можно искать какую-то скрытую причину этого или ошибочно предположить, что один круг служит причиной возникновения другого. Этот пример интересен еще и тем, что в XX в. физики усиленно выступали за модель пространственно изогнутого мира, представить который мы, к сожалению, не можем.

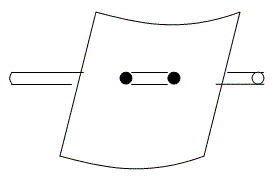
Рис. 7. Соломинка движется сквозь изогнутую плоскость

Эти примеры ясно показывают, что жители двухмерного мира могут исходить лишь из предположений. Они выстраивают целые теории по поводу наблюдаемых феноменов, совсем не понимая их. Не кажется ли вам, что в нашем трехмерном обычном мире происходит нечто подобное? Возможно, многие явления имеют своим источником некое другое измерение, которое мы, как правило, не воспринимаем. Много ли мы понимаем в том мире, который нас окружает?

Платон и его пещера

Вновь вернемся к третьему и четвертому измерениям. В последнем примере мы совсем близко подошли к мысли, что и в нашем обычном мире, который мы обозначаем или воспринимаем как трехмерный, могут существовать многие отделенные друг от друга объекты, которые в действительности являются проявлениями или проекциями одного-единственного(!) четырехмерного объекта. Наше пространство может быть изогнуто, как уже утверждают физики и математики. Логически завершая все вышесказанное, можно заключить, что два человека, которые независимо друг от друга появляются в трехмерном мире, — это лишь формы проявления одного и того же существа из четырехмерного мира! Иными словами, можно утверждать: «На самом деле все не так, как кажется!»

Платон в своем знаменитом «Мифе о пещере» создает замечательный образ («Государство», книга 7). Он сравнивает объекты и людей, которых мы видим, с тенями, возникающими на стене пещеры в тот момент, когда у одной из стен пещеры горит костер, а люди движутся между огнем и противоположной стеной. В его примере речь идет о пленниках, заключенных в пещере, "которые не могут видеть огня и потому считают тени на стене единственной реальностью. Одному из этих пленников все же удалось обернуться и увидеть огонь. Благодаря этому ему открылась ошибочность восприятия.

По мнению Платона, в реальном мире мы видим лишь тени людей, а не их самих, каковы они есть в действительности. Тень — это двухмерная проекция трехмерного объекта. Очевидно, реальность не полностью соответствует нашему восприятию. Подобно несчастным узникам в примере Платона, мы находимся в плену привычных заблуждений. Но возможно, что все же существует способ воспринять совершенно иную реальность такой, какова она есть в действительности.

Таким образом, проблема ошибочного восприятия следующих измерений была поставлена еще задолго до наших дней. Естествознание, не включающее ее в круг своих размышлений и экспериментов, без сомнения, является несовершенным. В нем есть много пробелов, тем более серьезных, что существуют феномены, которые оно вообще не может объяснить.

В действительности мы находимся в ситуации, подобной той, о которой рассказал Платон. Поскольку мы не можем постичь, что представляют собой последующие измерения, и не можем понять, как функционирует человеческое сознание, — да простят меня психологи! — мы, к примеру, не можем объяснить, как некоторые люди, используя особые способности, могут силой духа воздействовать на окружающие их материальные объекты. Точно так же современная наука не в состоянии объяснить, каким образом два человека практически моментально могут вступать в телепатический контакт, при этом находясь на любом расстоянии друг от друга. Различные феномены, связанные со временем, пока также не нашли объяснения, несмотря на многочисленные попытки втиснуть их в рамки уже известных моделей. Документально зафиксировано множество случаев, когда человек совершал прыжок во времени, как правило в прошлое, но в такой форме, которой, по нашим представлениям, вообще не может быть. Увлекательный материал по этой теме можно найти у Эрнста Мекленбурга. Один из описанных им случаев приведен, как уже упоминалось, в главе 13 «Прыжок во времени».

Чем может помочь компьютер?

После этого пространного отступления вновь вернемся к компьютеру. При создании каких гипотетических моделей следующих измерений он может оказаться полезным? К сожалению, его не удастся использовать для того, чтобы осмыслить четвертое измерение как временное,- по крайней мере в данный момент мы не представляем, как это возможно. Но это не значит, что у нас не появится такой возможности в будущем. Однако уже сегодня реально изображение четвертого измерения как следующего пространственного, то есть изображение четырехмерного пространства. Таким образом, мы можем отобразить на экране четырехмерные объекты.

Просто увидеть тела, которых не существует в трехмерном пространстве, можно как в Интернет, так и в книгах. Подобные картинки действительно занимательны, но для того, чтобы посмотреть на них, компьютер вовсе не обязателен. Типичный пример - так называемая бутылка Клейна (названная по имени немецкого математика Феликса Клейна), с которой уже давно знакомы математики. В одном из разделов математики, топологии, исследуются такие и еще более невообразимые тела и поверхности. Бутылка Клейна – одно из тел с самозамыкающейся поверхностью, внешняя сторона которых вдруг становится внутренней и наоборот.

Этот переход вполне представим графически. Однако в нашем трехмерном мире подобные объекты не могут существовать без того, чтобы их поверхность не была нарушена (например, там, где горлышко бутылки Клейна переходит в ее более широкую часть). Это постулирует наличие четвертого измерения, в котором существование подобных тел не вызывает никаких проблем.

Рис. 8. Бутылка Клейна

Лента Мебиуса и свободная энергия

Еще более простой пример, чем бутылка Клейна, причем вполне осуществимый на практике,- это лента Мебиуса (названная по имени немецкого математика и астронома Августина Фердинанда Мебиуса). Вы даже можете сами склеить ее из бумаги. Внутренняя и внешняя поверхности этой ленты незаметно переходят одна в другую. Не говоря о том, что эта простая конструкция всегда привлекала математиков, некоторые инженеры и физики уже давно обращали внимание на то, что электрические катушки в форме ленты Мебиуса обладают поразительными свойствами. Особенно заинтересовались этим теоретики и практики из университетов Японии. Машины, которые можно построить с использованием таких катушек, вырабатывают больше энергии, чем потребляют! Нарушение известного закона физики в этом случае оказывается мнимым, так как энергия поступает из так называемого вакуумного поля — области, которая хорошо известна физикам.

Возможно, вы еще в школьные годы забавлялись с кольцом, сделанным из полоски бумаги, которая перекручивается на 180°, а затем склеивается. Это и есть лента Мёбиуса.

Вы можете подумать: «Да, это занятно, но при чем тут другие измерения?» Но давайте попытаемся описать подобную ленту некоему воображаемому собеседнику: «Представь себе, эта лента имеет лишь одну поверхность, на которой не различаются верх и низ. Если вести линию карандашом, то через некоторое время попадешь "внутрь" ленты, а затем, не пересекая ни перегиба, ни края бумаги, вновь возвратишься в исходную точку. Для этой конструкции не существует понятий "внутри" и "снаружи"».

Это описание не подходит ни для одной из известных нам поверхностей, поскольку даже на шаре, где мы вновь возвращаемся в исходную точку, мы всё же не можем попасть на его внутреннюю сторону — у этой фигуры, безусловно, есть и «внутри», и «снаружи». В случае ленты Мёбиуса, кажется, нарушаются правила трех измерений. Может быть, это настоящий четырехмерный объект? Лишь размышляя над этой лентой, — даже без компьютера — можно запустить интересные процессы в сознании.

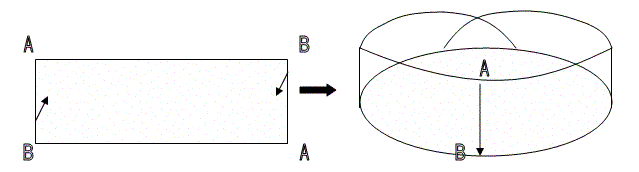
Рис. 9. Лента Мёбиуса

Такую ленту Мёбиуса в ее разнообразных модификациях можно найти и в Интернете. Тот, кто искушен в программировании, может создать ее на экране самостоятельно.

Если в школе или в университете вас учили, что лента Мёбиуса не может быть описана с помощью формул и поэтому недоступна для компьютера, забудьте об этом! Это неправда! Лента Мёбиуса задается очень простым уравнением и программируется в одно мгновение. Можно создавать ленты с любым числом перегибов и по-разному располагать их, например, так, чтобы они опоясывали воображаемый шар. Эти парадоксальные фигуры могут чрезвычайно эффективно использоваться в технике. Не обходят их вниманием и эзотерики — прежде всего из-за их возможного благотворного влияния на расширение сознания. Не исключено, что ленты Мёбиуса, используемые в технике в форме электрических катушек, могут разрушать обычную структуру нашего трехмерного пространства.

Вращающиеся четырехмерные тела — гиперкуб

Однако, чтобы использовать возможности компьютера, обратимся к вращающимся телам, которые могут более наглядно продемонстрировать, что такое следующие измерения. По этой теме существует немало готовых демонстрационных программ на дисках и в Интернете (см. список литературы и адресов в Интернете, приведенный в конце книги). Те, кто искушен в программировании, сами могут составить подобные программы. Принцип этих программ достаточно прост. Большинство программ такого рода основано на четырехмерном шестиграннике — гиперкубе. Этот куб, как правило, представляет собой постепенно поворачивающуюся на экране рамочную или стержневую конструкцию (в рамочной конструкции изображены лишь ребра, таким образом, углы куба связаны линиями, а плоскости домысливает воображение).

Как отобразить такую модель на плоском экране? Уже для трехмерного объекта, то есть обычного куба, мы сталкиваемся с проблемой отображения объемного объекта на плоском экране. Понятно, что это вполне возможно. Любая картина или фотография служит доказательством того, что зритель прекрасно может представить себе структуру пространства, если умело отобразить его на плоскости, то есть в двух измерениях. Наш глаз — это инструмент, который воспроизводит на сетчатке картину мира в двух измерениях. Лишь благодаря определенному угловому расстоянию между глазами мозг способен создавать трехмерную картину. Однако этому тоже сперва нужно научиться, о чем свидетельствуют наблюдения над маленькими детьми, которые сначала воспринимают просто цветовые пятна и лишь со временем начинают выделять предметы и определять расстояния. Поначалу они даже не могут оптически отделить себя от окружающего мира.

Итак, если мы захотим представить обычный трехмерный куб вращающимся на экране, мы должны рассчитать постоянно изменяющиеся проекции на плоскости. Это довольно просто. Для четырехмерного куба предстоит решить схожую проблему. Но как хотя бы частично представить себе четырехмерный куб?

Возможно, сделать это нам поможет метод, с помощью которого мы из квадрата получаем обычный куб. Если нарисовать квадрат, а затем над ним — еще один такой же, но немного сдвинутый (так, чтобы при этом расстояние между верхним и нижним квадратами было равно длине стороны этого квадрата), то мы получим рамочную модель куба. Таким образом, куб возникает в результате того, что мы поднимаем квадрат вверх, в следующее, третье, измерение. Из четырех углов квадрата при этом получается восемь углов куба.

Рис. 10. Как получить куб из квадрата

Точно так же можно представить, как выдвинуть из трехмерного куба еще один такой же и соединить между собой углы этих двух кубов. Получившаяся на этот раз фигура будет уже четырехмерной, и потому ее нельзя увидеть, а можно, в лучшем случае, представить теоретически.

Рис. 11 может дать о ней лишь самое общее представление.

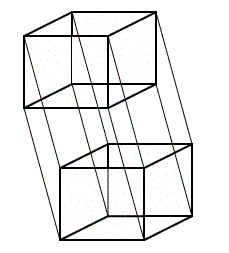
Рис. 11. Как получить четырехмерный куб из трехмерного

Обычный куб на плоскости представляет собой развертку из шести квадратов. Четырехмерный куб также можно представить в виде развертки из шести трехмерных кубов — как раз ее изобразил Сальвадор Дали на картине «Распятие (тело—гиперкуб)». Четырехмерный куб можно точно рассчитать. У него 16 углов, 34 ребра, 28 обычных плоскостей и 8 гиперплоскостей, которые обычно невозможно изобразить. Но кое-что можно сделать с помощью специальной программы.

Как правило, при повороте тела в пространстве поворот изображения на экране вокруг любой из осей рассчитывается таким образом, чтобы можно было последовательно осуществить несколько поворотов вокруг трех осей. Эти взаимно перпендикулярные оси поворота подобны осям координатной системы, о которой шла речь в начале главы. В четырехмерном пространстве таких осей больше, но для рассчитывающей программы это не составляет проблемы. Интересно поразмышлять, как следует изобразить вершины и ребра (в рамочной модели).

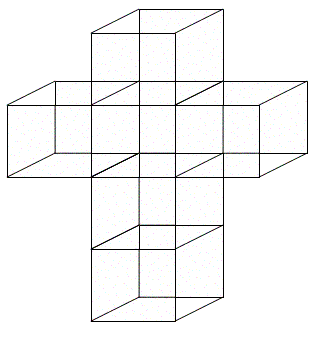
Рис. 12. Развернутый четырехмерный гиперкуб

Обычно вершина задается тремя координатами (длиной, шириной и высотой), которые точно определяют положение точки в пространстве. Для представления на экране одну из этих координат можно просто убрать, потому что двух оставшихся будет вполне достаточно. При изображении четырехмерного объекта можно отбросить даже две координаты — но какие? Еще интереснее, когда речь идет о ребрах, которые, как известно, представляют собой линию, связывающую две вершины. Вершины гиперкуба могут быть связаны между собой множеством способов (для математиков: 32!), которых можно насчитать 263130836933693530167218012160000000, то есть около 263 секстиллиардов.

Таким образом, следует выбрать некоторые из 32 ребер. В результате мы получим потрясающее, постоянно изменяющееся изображение гиперкуба, который при повороте всегда остается загадкой и не соотносится ни с одним известным объектом: мы просто не понимаем, ЧТО вращается на экране. Однако почти все, кто имел дело с этой программой хотя бы как зритель, единодушно утверждают, что постепенно начинали понимать, как может быть устроен подобный объект. Рассматривая его, некоторые люди даже переживают удивительное состояние и почти впадают в транс. У них возникает ощущение, что их пространственное восприятие расширилось. Этот невозможный и все же возможный вид гиперкуба просто опровергает наше обычное восприятие и нашу картину мира. Очевидно, постепенно благодаря этому активизируются области мозга, до этого не использовавшиеся. Кто говорит о том, что мы не можем воспринимать четвертое измерение? Мы просто этому не обучены!

В этом смысле программа с гиперкубом действует так же, как коаны в дзэн-буддизме. Коаны — это особые вопросы, которые наставники задают своим ученикам. Ответить на них, используя нашу привычную логику, просто невозможно. Пытаясь найти ответ, ученик достигает такого состояния, когда освобождаются области сознания, остававшиеся до этого без применения, — вполне возможно, что они способны воспринимать и измерения, лежащие за пределами нашей привычной картины мира. В качестве примера таких кознов можно привести вопросы: «Каким будет звук от хлопка одной ладони?» или «Какова величина числа минус единица?». (Отрицательные числа, как в данном случае минус единица, не существуют на самом деле и не могут использоваться для подсчета предметов и т. п.). В результате раздумий над подобными вопросами — или, лучше сказать, сосредоточения на заданной теме — происходит прорыв в сознании и человек достигает нового, доселе неизвестного состояния просветления.

Хотя программирование вращающегося гиперкуба довольно несложно, подобные программы существенно расширяют восприятие действительности. Полученный при этом опыт может вдохновить вас на то, чтобы заняться бесконечными возможностями нашего мозга и нервной системы. Западные ученые и мудрецы Востока единодушны в том, что средний человек использует лишь 5 — 10% своего духовного потенциала. Остальное просто не востребовано. Как на Востоке, так и на Западе созданы методики, позволяющие в гораздо большей степени задействовать наши духовные возможности. Если мы хотим двигаться в этом направлении, оптимально было бы следовать традиционными путями⁹. Все они предлагают множество методов и прежде всего обращают внимание на гармоничное развитие ума, духа и тела. Пользоваться при этом наставлениями учителя отнюдь не возбраняется, а для начинающих даже весьма желательно. Позже, уже пройдя некоторый отрезок пути, вы заметите, что возросшие возможности восприятия — это лишь незначительная часть того, что предстоит открыть и развить в духовно-умственной сфере.

1 Benoot Mandelbrot. Die fraktale Geometric der Natur. Basel, 1987.

2 Paramahamsa Yogananda. Autobiographic eines Yogi. Bern, 1975.

3 Takpo Tashi Namgyal. Mahamudra. Delhi: Motilal Banarsidass Publishers, 1993

4 Yoga philosophy of Patanjali/Commentary by Swami Hariharananda Aranya. University of Kalkutta, 1977

5 On the Way to Understanding the Time Phenomenon/A.P. Levich (Hg.): World Scientific Publiching Company, September 1995.

6 Preston B. Nichols, Peter Moon. Das Montauk-Projekt. E. T. Publishing Unlimited, 1994.

7 Peter D. Ouspensky. Tertium Organum. Munchen, 1973.

8 Edwin A. Abbott. Flatland. Dover Publications 1992 (Originalausgabe 1884); Flachenland, Laxenburg / Osterreich, 1999.

9 На Востоке - это учения йоги, цигун, тантризма. На Западе - это пути розенкрейцеров, антропософов, свободных каменщиков. Индейцы Северной и Южной Америки также обладают богатым и своеобразными духовными традициями. На Ближнем Востоке - это суфизм.