3. Понятие линейного программирования
3. Понятие линейного программирования
Задача линейного программирования в общем виде может быть сформулирована следующим образом. Требуется найти экстремум (максимум или минимум) целевой функции
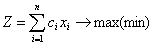 , (2.1)
, (2.1)
при ограничениях:
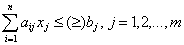 , (2.2)
, (2.2)
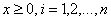 . (2.3)
. (2.3)
где сi - затраты в случае минимизации или доход в случае максимизации;
aij - удельные затраты j-го ресурса на единицу выпуска i-го продукта;
bj - лимиты ресурсов или количественное выражение спроса в зависимости от смыслового наполнения величины bj;
xi - искомые количества i-го продукта.
Система ограничений (2.2) означает, что в случае ограниченности ресурсов их расход не может быть превышен (ограничения со знаком <=), или в случае трактовки bj как характеристик спроса (ограничения со знаком >=), означает, что потребности (спрос) должны быть полностью удовлетворены или превышены.
Система ограничений (2.3) - традиционные ограничения на известные с экономическим смыслом, т.е. либо искомые объекты продукции выпускаются (xi > 0), либо нет (xi = 0).
Упорядоченная совокупность чисел (вектор) (x1, x2, ..., xn), которая удовлетворяет ограничениям (2) и (3), называется допустимым решением (планом) задачи линейного программирования.
3.1 Пример решения задачи линейного программирования
На предприятии планируется производство двух новых изделий: А и В.
| Для изготовления требуется | Изделие А | Изделие В |
| Материал 1, кг | 1 | 3,5 |
| Материал 2, кг | 2 | 0,5 |
| Трудозатраты, чел./день | 1 | 1 |
| Имеющиеся ресурсы | ||
| Материал 1, кг | 350 | |
| Материал 2, кг | 240 | |
| Трудозатраты, чел./день | 150 |
Требуется определить, сколько изделий А и В необходимо изготовить, чтобы обеспечить максимальную прибыль, если прибыль от реализации изделия А составляет 10 у.е., а изделия В - 20 у.е. При этом необходимо обеспечить выпуск не менее 60 изделий В.
Составляем экономико-математическую модель задачи, для чего введем следующие обозначения:
x1 - количество изделий А;
х2 - количество изделий В;
Тогда целевую функцию можно представить:
Z(х) = 10 x1 + 20 х2 → max.
Ограничения задачи можно записать следующим образом:
x1 + х2 ≤ 150
2 x1 + 0,5 х2 ≤ 240
x1 + 3,5 х2 ≤ 350
x1 ≥ 60
х2 ≥ 0
Фрагмент листа Excel, подготовленный для решения рассматриваемой задачи, показан на рис. 1

Рис. 1.
Оптимальные значения выпуска изделий будут выведены в ячейки A2, B2.
Оптимальное значение целевой функции - в ячейку C3.
Правые части ограничений находятся в ячейках D4:D7, коэффициенты целевой функции - в ячейках A3:B3, коэффициенты при переменных в ограничениях - в ячейках A4:B7.
В ячейку C3 при помощи Мастера функций вводим формулу для расчета целевой функции (из категории Математические выбираем функцию СУММПРОИЗВ). Данные, вводимые для работы функции СУММПРОИЗВ, показаны на рис. 2. Т.к. данные из массива 1 будут использоваться при вводе зависимостей для всех ограничений, используются абсолютные ссылки на ячейки этого массива. Копируем содержание ячейки C3 в ячейки C4:C7.
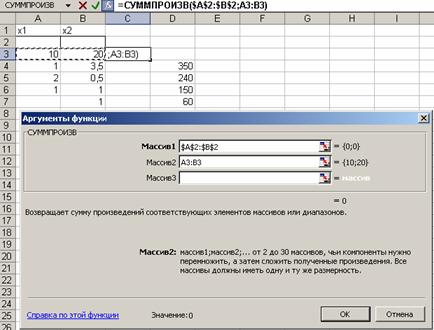
Рис. 2.
Для поиска оптимального решения воспользуемся возможностями средства Excel - Поиск решения, предназначенного для выполнения сложных вычислений при поиске целевой функции с учетом до 200 переменных, удовлетворяющих заданным пользователем критериям. Запуск процесса поиска решения осуществляется командой Сервис/Поиск решения. После чего на экране появляется диалоговое окно, которое необходимо заполнить в соответствии с условиями решаемой задачи (рис. 3).
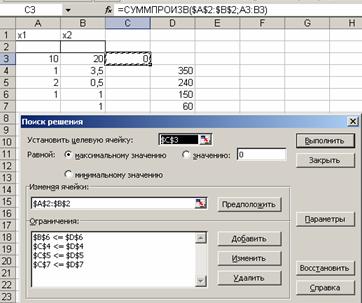
Рис. 3.
В окне для ввода адреса целевой ячейки задаем абсолютный адрес ячейки C3.
Средство Поиск решения обеспечивает поиск оптимального значения в указанной ячейке в соответствии с заданными ограничениями. Отметим, что целевая ячейка связана с другими ячейками рабочего листа с помощью формул.
В окне Изменяя ячейки - абсолютные адреса ячеек A2, B2, в которых будет располагаться параметры, изменяемые в ходе процесса оптимизации результата, находящегося в целевой ячейке. В нашем примере, для поиска оптимальной прибыли мы изменяем возможные объемы выпускаемых изделий А и В.
В окне Ограничения вводим ограничения, формализованные при составлении экономико-математической модели решаемой задачи.
При помощи кнопки Параметры диалогового окна Поиск решения уточняем задаваемые параметры поиска (рис. 4).
В нашем примере, в частности, задаем опцию Линейная модель (используется симплекс-метод) и опцию Допускаются неотрицательные значения.
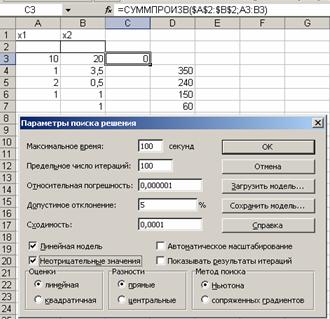
Рис. 4.
Кнопка Выполнить диалогового окна Поиск решения позволяет получить результат решения задачи, который показан на рис. 5.
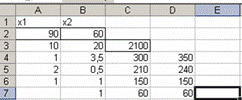
Рис. 5.