В начало

Дифференциальное исчисление функций одной переменной

Элементы аналитической геометрии и линейной алгебры

Задача 1

На предприятии для производства трех видов изделий установлены три технологические производственные линии для их изготовления. Владелец предприятия стремится полностью использовать эти линии в течение 8-ми часовой рабочей смены. Данные о том, сколько времени (в часах) должна эксплуатировать та или иная линия для изготовления одного изделия каждого вида, приведены в матрице А = (а_ij)

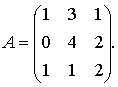
Величина элемента а_ij представляет собой затраты времени (в часах) i-ой линии для изготовления единицы j-го изделия. Взяв в качестве неизвестных х₁, х₂ и х₃, составить систему уравнений, предполагающую полное использование линий. Найти с помощью обратной матрицы решение полученной системы.

Решение

Обозначим число изделий 1-ого, 2-ого и 3-ого видов через х₁; х₂; х₃. Рассмотрим работу каждой из линий: для первой линии при изготовлении х₁ изделий 1-ого вида затрачивается 1 х₁ часов, х₂ изделий 2-ого вида 3 х₂ часов и х₃ изделий 3-го вида 1 х₃ часов. По условию задачи первая линия работает 8 часов, поэтому имеем уравнение:

х₁ + 3х₂ + х₃ = 8.

Аналогично для 2-ой линии:

4х₂ + 2х₃ = 8,

и для 3-ей линии:

х₁ + х₂ + 2х₃ = 8.

Решение исходной задачи сведено к нахождению решения системы трех линейных уравнений с тремя неизвестными:

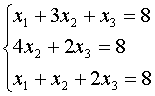
Решим эту систему с помощью обратной матрицы, записав ее предварительно в матричной форме (см. [1], стр. 39, формула 2.3)

АХ = В,

Где А - матрица коэффициентов при переменных, а Х и В - матрицы-столбцы переменных и свободных членов.

В нашем случае:

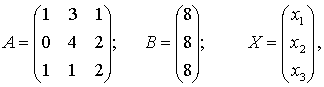
таким образом, в матричной форме система имеет следующий вид:

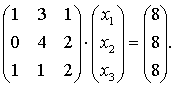
Уравнение можно решить, если матрица А - неособенная, так как в этом случае существует обратная матрица А^-1 и

Х = А^-1В.

Для нахождения матрицы А^-1 необходимо, прежде всего, вычислить определитель матрицы А и убедиться в том, что она - неособенная. Для этого воспользуемся теоремой Лапласа (см. [1], формула 1.9)

,

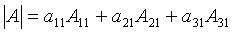где А_ij - алгебраические дополнения элементов а_ij матрицы А.

Используя определение, получим

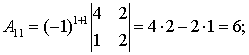
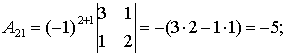
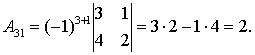
Следовательно,

.

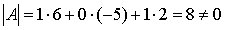Комментарий. Заметим, что алгебраическое дополнение А₂₁ можно было бы здесь и не находить, так как а₂₁ = 0.

Продолжение решения

Итак, |A| = 8 ≠ 0. Следовательно, матрица А неособенная, и для нее существует обратная матрица

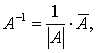
где 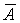- матрица, присоединенная к матрице А.

В нашем случае:

Элементы первой строки матрицы 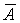уже найдены. Находим остальные элементы:

; ; ;

; ; .

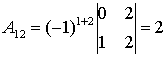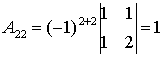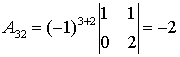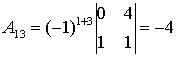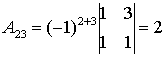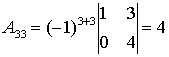Таким образом, присоединенная матрица:

.

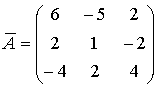Зная 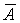и |A|, находим обратную матрицу A^-1:

.

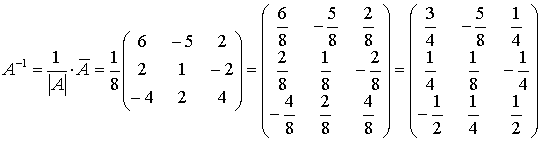Мы воспользовались определением произведения матрицы на число, в нашем случае равное 1/8 (см. [1], стр. 11).

Проверим правильность вычислений, т.е. что AA^-1 = E, где E- единичная матрица 3-го порядка. По определению произведения матриц получим:

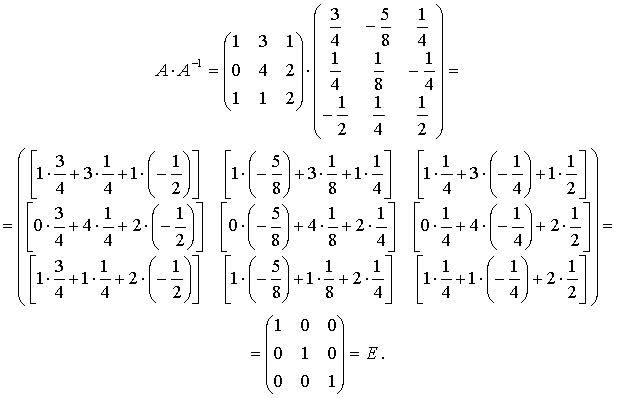
Проверка подтвердила правильность найденной нами матрицы.

И, наконец, находим матрицу-столбец неизвестных:

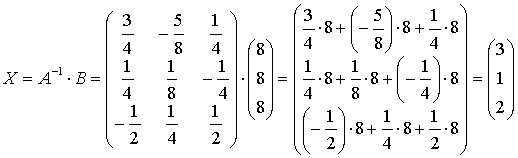
Итак, х₁ = 3; х₂ = 1; х₃ = 2. Сделаем проверку, подставив найденное решение в каждое уравнение системы.

Проверка:

3 + 3 × 1 + 2 = 8; 8 = 8

4 × 1 + 2 × 2 = 8; 8 = 8

3 + 1 + 2 × 2 = 8; 8 = 8

Итак, мы видим, что после подстановки в систему каждое уравнение обратилось в числовое тождество.

Ответ. Будет произведено 3 изделия 1-ого вида, 1 изделие 2-ого вида и 2 изделия 3-его вида.

Вопросы для самопроверки

1. Сформулируйте правила вычисления определителей второго и третьего порядка.
2. Сформулируйте основные свойства определителей.
3. Сформулируйте теорему Лапласа о разложении определителя по строке (столбцу).
4. Дайте определения основных действий над матрицами: произведения матрицы на число, суммы, произведения.
5. Дайте определение единичной матрицы порядка п.
6. Какая матрица называется присоединенной к матрице А?
7. Дайте определение матрицы, обратной для данной квадратной матрицы.
8. Запишите формулу для нахождения обратной матрицы.
9. Что называется решением системы линейных уравнений?

Задачи № 01 - 20

Решить следующие системы линейных уравнений в матричной форме.