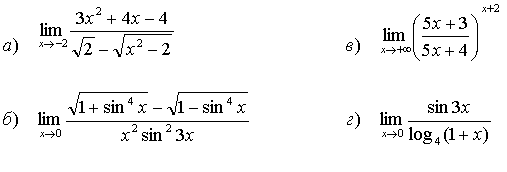В начало

Дифференциальное исчисление функций одной переменной

Введение в математический анализ

Задача 2

Найти предел:

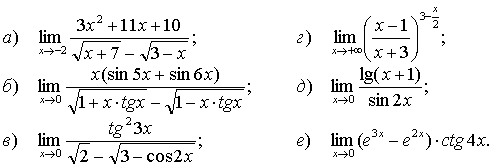
Решение:

а) Функция, предел которой при x → -2 требуется найти, представляет собой частное двух функций. Однако применять теорему о пределе частного (см. [1], стр. 154) в данном случае нельзя, так как предел функции, стоящей в знаменателе, при x → -2 равен нулю.

Преобразуем данную функцию, умножив числитель и знаменатель дроби, находящейся под знаком предела, на выражение 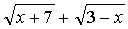, сопряженное знаменателю. Параллельно разложим квадратный трехчлен в числителе на линейные множители:

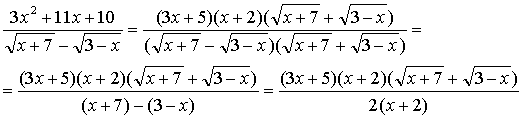
Сокращая теперь числитель и знаменатель последней дроби на общий множитель x + 2, получим новую функцию

,

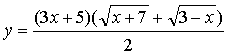которая отличается от данной значением лишь в одной точке x = -2: данная функция в этой точке не определена, а новая определена и непрерывна как элементарная функция. Поскольку переопределение функции в одной точке не сказывается на значении предела и поскольку для функции, непрерывной в точке x₀, ее предел при x → x₀ равен значению этой функции в точке x₀ (см. [1], стр. 161), то

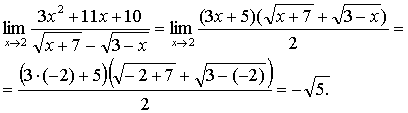
б) И в этом примере начнем преобразования с умножения числителя и знаменателя дроби, стоящей под знаком предела, на выражение, сопряженное к знаменателю:

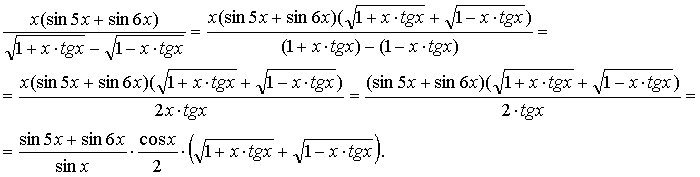
Заметим, что пределы в нуле второго и третьего сомножителей как непрерывных в нуле функций равны их значениям в этой точке:

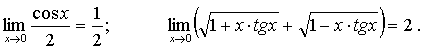
Чтобы найти предел первого сомножителя, разделим его числитель и знаменатель на x:

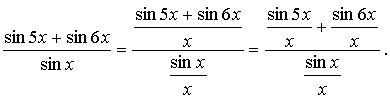
Предел

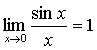
есть первый замечательный предел (см. [1], стр. 156). Пределы

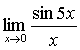и

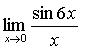
легко сводится к нему. Например,

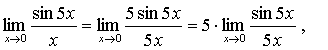
и после замены t = 5x:

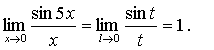
Следовательно, 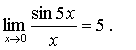Аналогично,

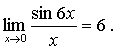
Теперь с помощью теорем о пределе частного и суммы (см. [1], стр. 154) вычисляем предел первого сомножителя:

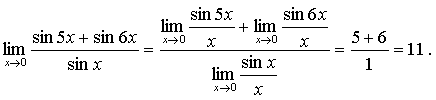
Воспользовавшись, наконец, теоремой о пределе произведения (см. [1], стр. 154), окончательно получаем:

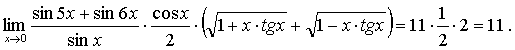
в) Избавляясь от иррациональности в знаменателе (так же, как и при предыдущих двух примерах) и применяя формулу 1 - cos2x = 2sin²x, будем иметь:

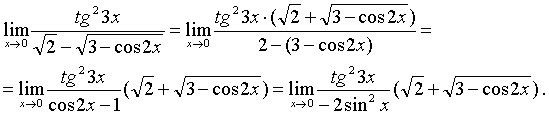
Предел функции 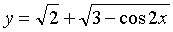в точке х=0 найдем, воспользовавшись непрерывностью этой элементарной функции в нуле:

.

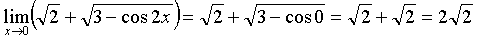Предел функции 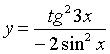в точке х=0 найдем, разделив предварительно числитель и знаменатель дроби в правой части равенства на x² и используя основные свойства предела (см. [1], стр. 154):

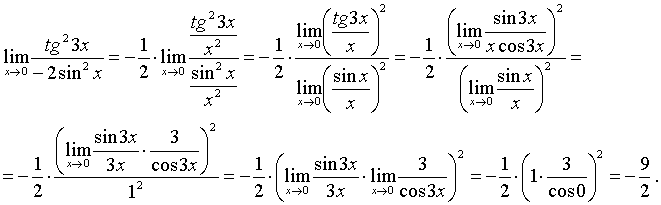
Теперь, применяя теорему о пределе произведения, получим:

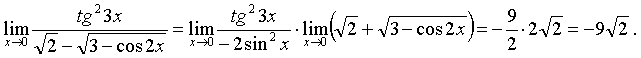
г) Прежде всего, преобразуем основание данной степенно-показательной функции:

.

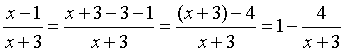Введем новую переменную

.

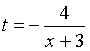Тогда

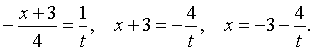
Заметим, что предел функции t при x → +∞ равен нулю, то есть t → 0 при x → +∞.

Следовательно,

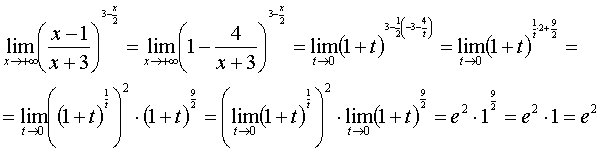
В конце мы воспользовались теоремой о пределе произведения, следствием теоремы о пределе сложной функции (см. [1], стр. 154), вторым замечательным пределом (см. [1], стр. 157) и непрерывностью в нуле функции y= (1 + t)^9/2.

д) Разделим числитель и знаменатель дроби, стоящей под знаком предела, на х:

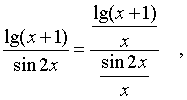
и рассмотрим пределы в нуле числителя и знаменателя получившейся большой дроби:

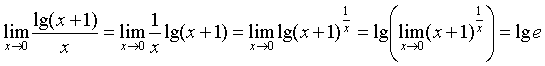
и

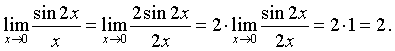
Используя, наконец, теорему о пределе частного, получим:

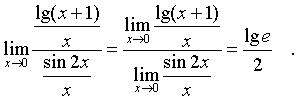
е) Представим выражение под знаком предела в виде

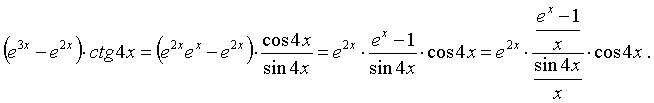
Легко находим:

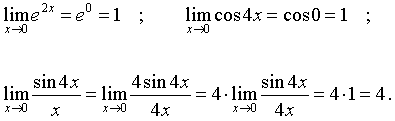
Для вычисления предела функции 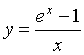при x → 0 введем новую переменную t = e^x - 1. Тогда

e^x = t + 1, x = ln(1+t),причем предел в нуле непрерывной функции t = e^x - 1 равен значению этой функции в нуле: e^x - 1 = 1 - 1 = 0, то есть t → 0 при x → 0. Следовательно,

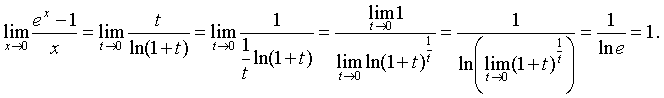
Применяя теоремы о пределе произведения и частного, окончательно получаем:

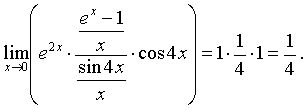
Вопросы для самопроверки

1. Что называется функцией? Каковы способы ее задания?
2. Что называется областью определения функции?
3. Что называется графиком функции?
4. Дайте определение конечного предела функции в точке. Дайте определения конечного предела функции при x → +∞ и при x → -∞.
5. Как связаны понятия: «предел функции в точке» и «пределы функции в точке слева и справа»?
6. Что такое бесконечно малая величина? Сформулируйте основные теоремы о бесконечно малых величинах.
7. Что такое бесконечно большая величина и как она связана с бесконечно малой?
8. Сформулируйте основные теоремы о пределах.
9. Напишите первый и второй замечательные пределы. Какие теоремы о пределах используются при их вычислении?
10. Дайте определения функции, непрерывной в точке и на отрезке.
11. Сформулируйте основные теоремы о непрерывных функциях.
12. Какие типы точек разрыва функции Вы знаете? Приведите примеры.

Задачи 21 - 40

Найти предел:

21.

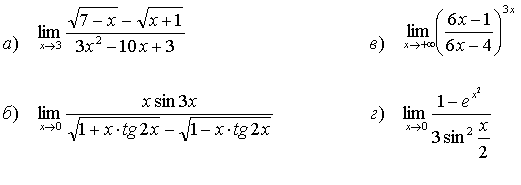
22.

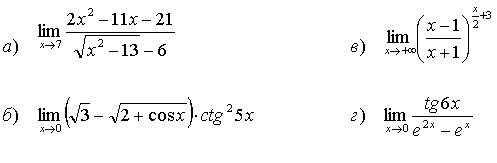
23.

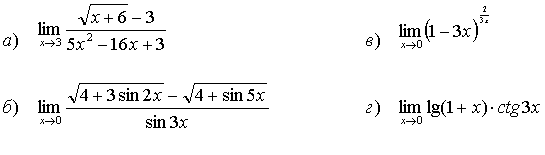
24.

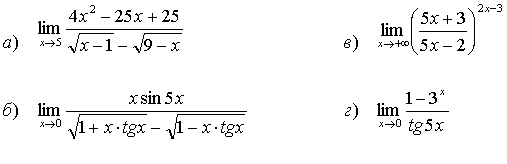
25.

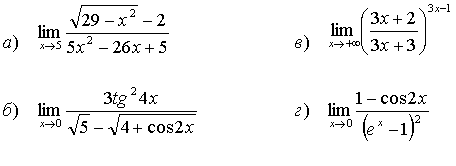
26.

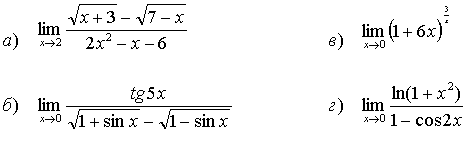
27.

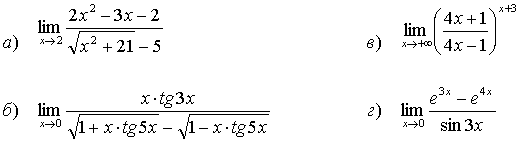
28.

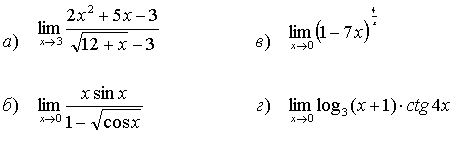
29.

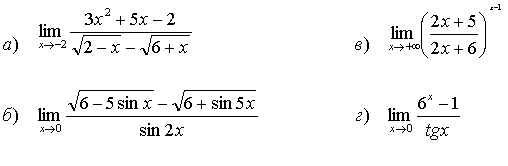
30.

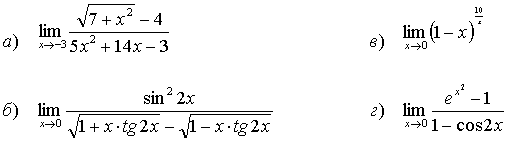
31.

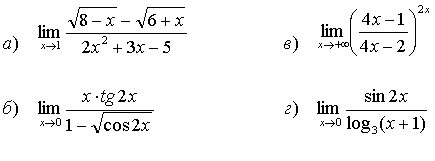
32.

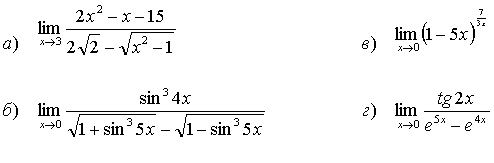
33.

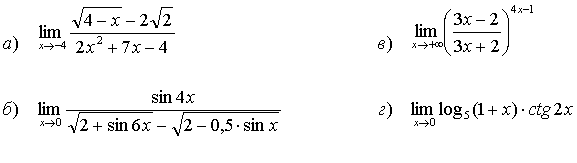
34.

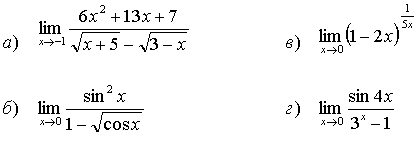
35.

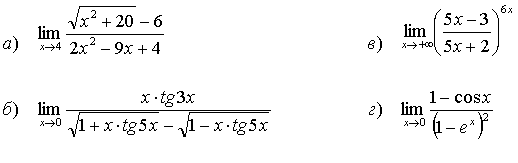
36.

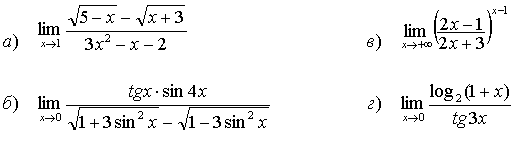
37.

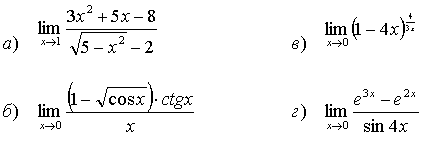
38.

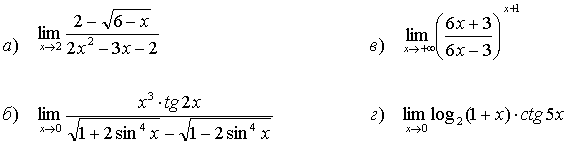
39.

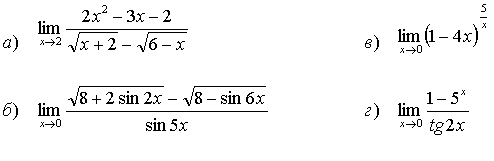
40.