Элементы аналитической геометрии и линейной алгебры
Дифференциальное исчисление функций одной переменной
Задача 3
Найти производную функции:
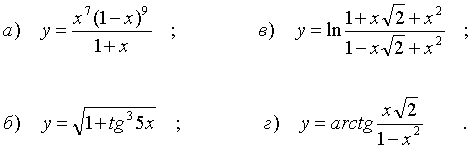
Решение:
а) Функция представляет собой частное двух функций. Ее производная по правилу дифференцирования частного (см. [1], стр. 183, формула 7.15) равна:
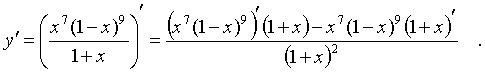
Выражение x7(1 - x)9 есть произведение двух функций x7 и (1 - x)9. Применяя правило дифференцирования произведения (см. [1], стр. 183, формула 7.12), имеем:
(x7(1 - x)9)' = (x7)'(1 - x)9 + x7((1 - x)9)'.Производная (x7)' = 7x6. Функция (1 - x)9 есть сложная функция, поэтому ее производная (см. [1], стр. 183, формула 7.16) равна:
((1 - x)9)' = 9(1 - x)8(1 - x)' = 9(1 - x)8((1)' - (x))' = 9(1 - x)8(0 - 1) = -9(1 - x)8Производную функции (1 - x) нашли, используя формулы дифференцирования суммы двух функций. Аналогично, (1 + x)' = 0 + 1 = 1..
Собирая все результаты, получим:
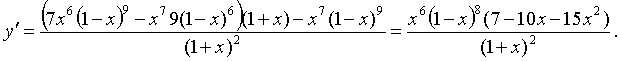
б) Преобразуем нашу функцию:
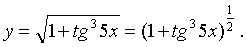
Это сложная функция. Взяв за аргумент u = 1 + tg35x и применяя последовательно правила дифференцирования сложной функции и производную тангенса, получим:
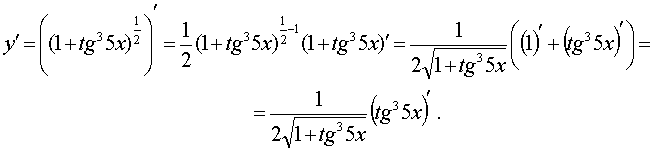
Итак, окончательно имеем:
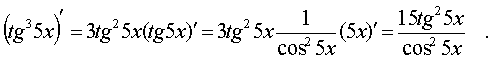
Окончательно получим:
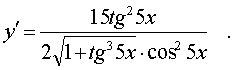
в) Наша функция есть сложная логарифмическая, в которой аргументом
является выражение 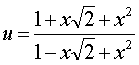 . Применив формулу производной
логарифмической функции (см. [1], стр. 188), получим:
. Применив формулу производной
логарифмической функции (см. [1], стр. 188), получим:
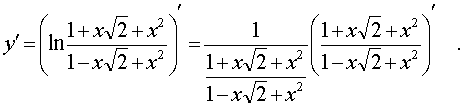
Далее нам нужно найти производную частного двух функций. По формуле производной частного имеем:
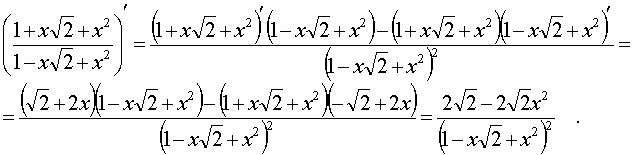
Окончательно получим:
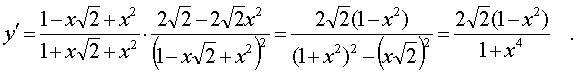
г) Вычисляем по формуле производной сложной функции, приняв
за аргумент выражение 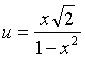 , получим:
, получим:
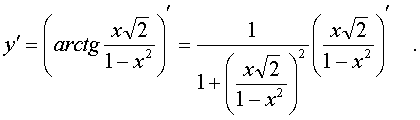
Воспользовавшись формулой производной для частного двух функций и делая необходимые преобразования, получим:
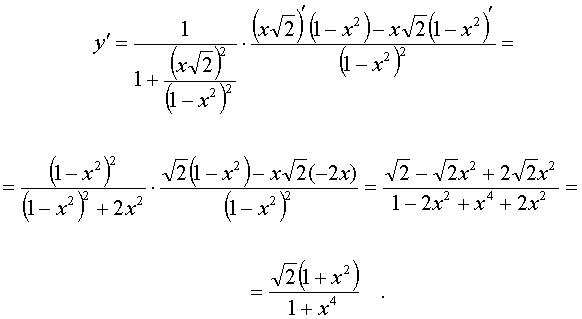
Вопросы для самопроверки:
- Что называется производной функции? Найдите производную функции y = x3, пользуясь только определением производной.
- Что называется касательной к кривой в данной точке? Каков геометрический смысл производной? Как составить уравнение касательной?
- Каков механический смысл производной?
- Каков экономический смысл производной?
- Будет ли функция непрерывна в точке, если она в ней дифференцируема?
- Перечислите правила дифференцирования и формулы дифференцирования основных элементарных функций.
- Производная сложной функции.
- Что называется дифференциалом функции? Его основные свойства.
- Каков геометрический смысл дифференциала функции в точке при заданном приращении аргумента?
- Какие свойства дифференциала функции Вы знаете?
Задачи 41 - 60
Найти производные функций:
41.
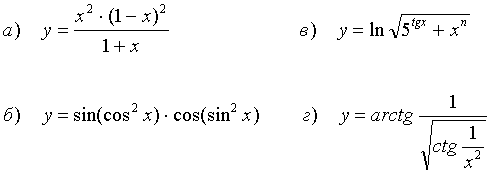
42.
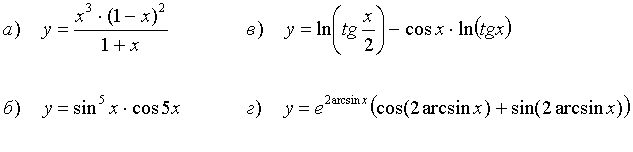
43.
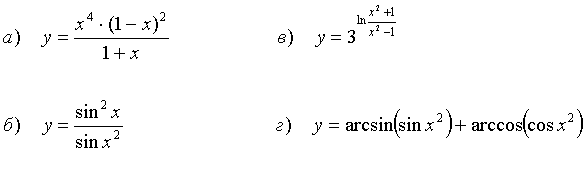
44.
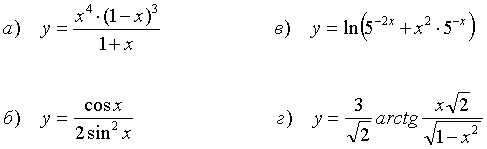
45.
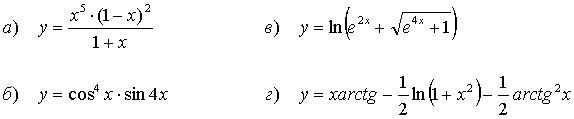
46.
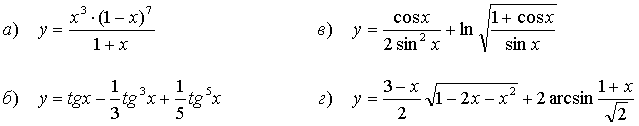
47.
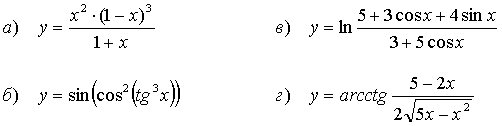
48.
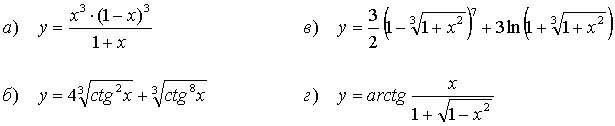
49.
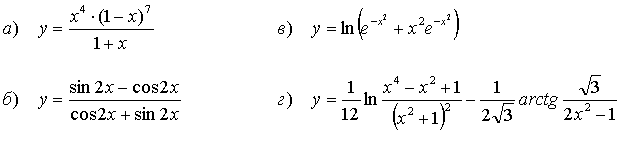
50.
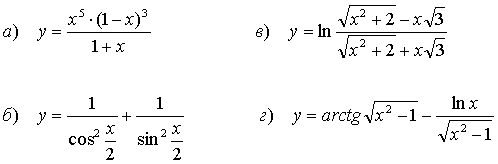
51.
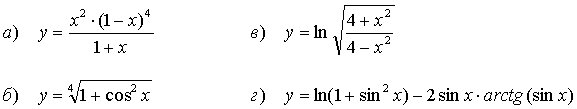
52.
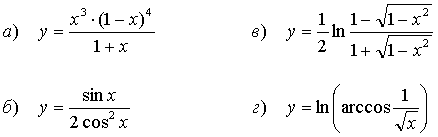
53.
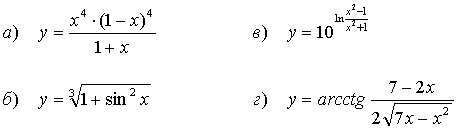
54.
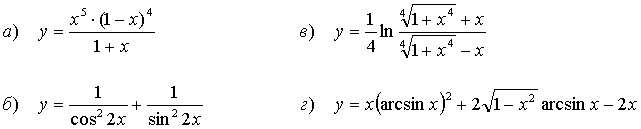
55.
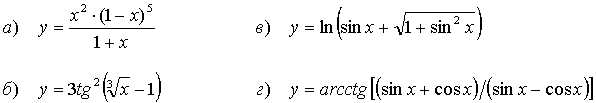
56.
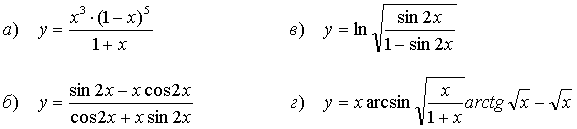
57.
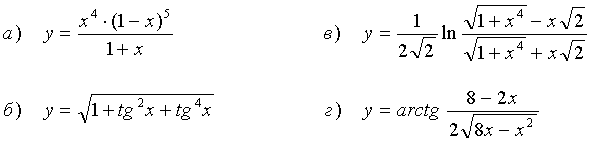
58.
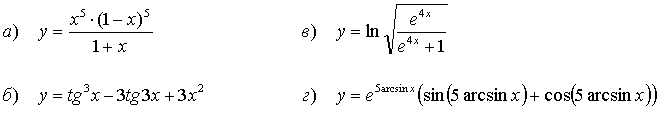
59.
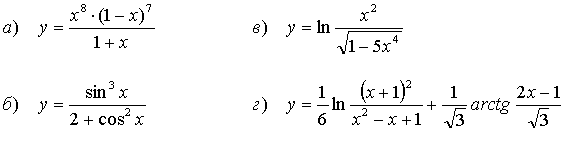
60.
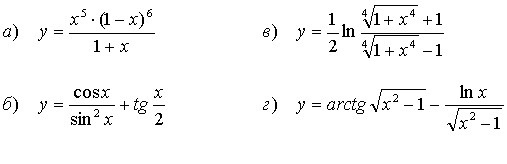
Задача 4
Найти неопределенные интегралы:
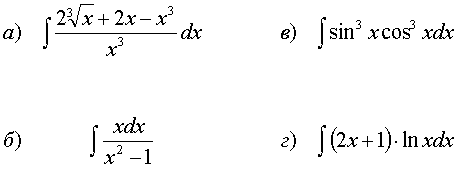
Решение:
а) Представим подынтегральную функцию в виде алгебраической суммы трех слагаемых. Для этого разделим почленно числитель на знаменатель:
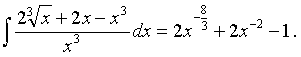
Неопределенный интеграл алгебраической суммы функций равен алгебраической сумме неопределенных интегралов этих функций (см. [1], стр. 253). Пользуясь этим свойством неопределенного интеграла и соответствующей формулой (см. [1], стр. 255, формула 10.7), получим:
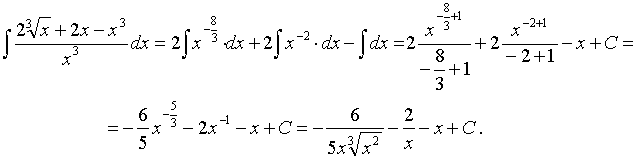
б) При нахождении этого интеграла воспользуемся методом подстановки. Введем новую переменную t = x2 - 1.
Тогда:
dt = d(x2 - 1) = (x2 - 1)' = (2x - 0)dx = 2xdx.
Отсюда 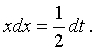
По формуле 10.8 (см. [1], стр. 255) имеем:
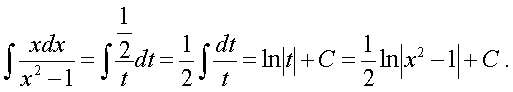
в) Для вычисления этого интеграла преобразуем подынтегральную функцию следующим образом:
sin3xcos3x = sin3xcos2xcosx = sin3x(1 - sin2x)cosx.
Поэтому
∫sin3xcos3x = ∫sin3x(1 - sin2x)cosxdx.
Сделаем замену t = sinx. Тогда dt = dsinx = cosxdx. Поэтому
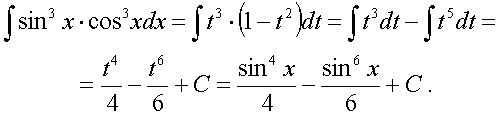
г) Для нахождения этого интеграла воспользуемся формулой интегрирования по частям:
∫udv = uv - ∫vdu
(см. [1], стр. 263, формула 10.21).
Положим u = lnx; dv = (2x + 1)dx,
тогда 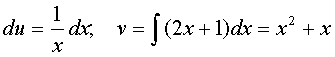 (постоянную С здесь можно
опустить).
(постоянную С здесь можно
опустить).
Подставив значения u; du; v; dv в формулу интегрирования по частям, получаем:
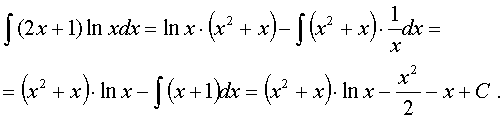
Вопросы для самопроверки:
- Какая функция называется первообразной данной функции?
- Что называется неопределенным интегралом от данной функции?
- Запишите таблицу простейших интегралов.
- Как производится замена переменной в неопределенном интеграле?
- Как производится интегрирование по частям в неопределенном интеграле?
- Назовите основные свойства неопределенного интеграла.
Задачи 61 - 80
Найти неопределенный интеграл:
61.
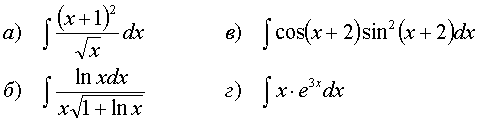
62.
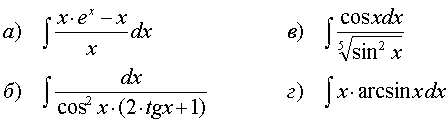
63.
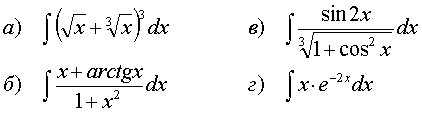
64.
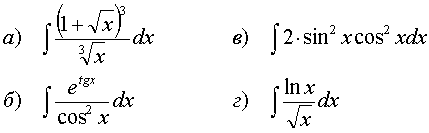
65.
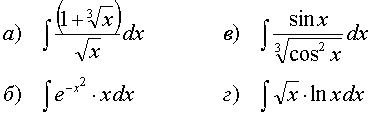
66.
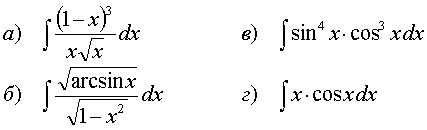
67.
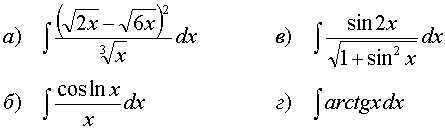
68.
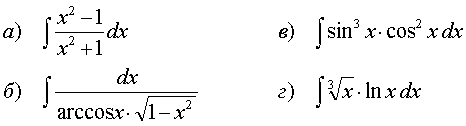
69.
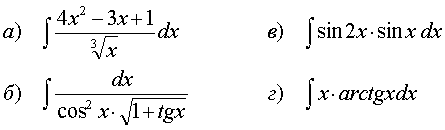
70.
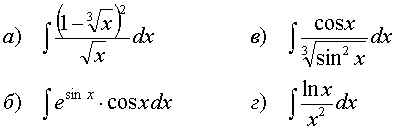
71.
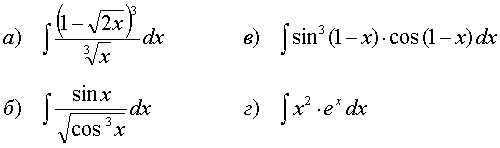
72.
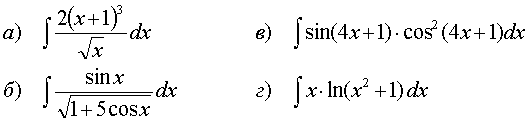
73.
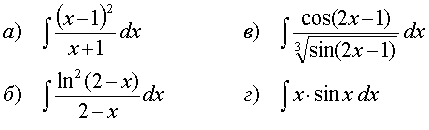
74.
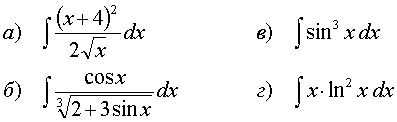
75.
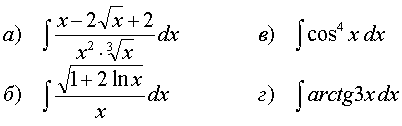
76.
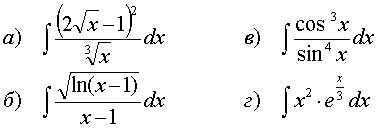
77.
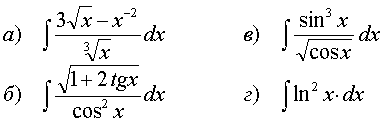
78.
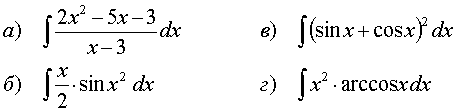
79.
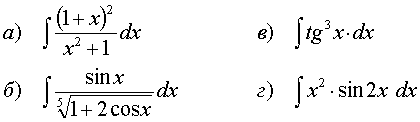
80.
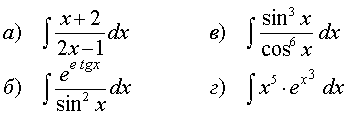
Задача 5
Вычислить площадь фигуры, ограниченной линиями y = x2 - 2x и y = -2x2 + x.
Решение:Чтобы наглядно представить фигуру, площадь которой надо найти, начертим графики функций y = x2 - 2x и y = -2x2 + x.
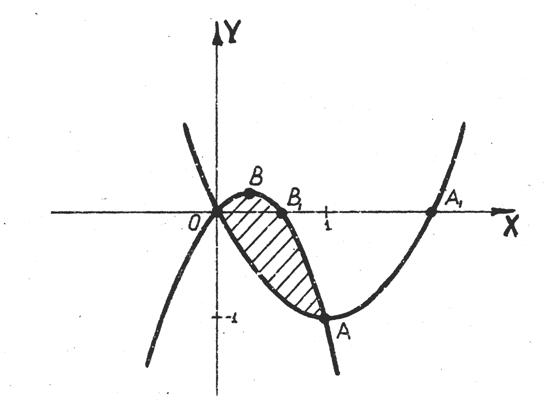
Рис. 1
Для построения параболы y = x2 - 2x определим координаты ее вершины и точек пересечения с осями координат. Выделив полный квадрат y = x2 - 2x = (x - 1)2 - 1, получим координаты вершины параболы A(1; -1). Ветви параболы направлены вверх, так как коэффициент при x2, равный 1, положителен. Точки пересечения параболы с осью абсцисс найдем, решив квадратное уравнение x2 - 2x = 0. Корни этого уравнения x1 = 0; x2 = 2. Получили точки O(0; 0); A1(2; 0). Точка пересечения с осью ординат находится при x = 0. Эта точка совпадает с точкой А. Для построения второй параболы y = -2x2 + x необходимо провести аналогичные действия. Получим вершину B(1/4; 1/8) и точки O(0; 0); B1(1/2; 0). Ветви этой параболы направлены вниз, так как коэффициент при x2 отрицателен. На рисунке 1 построены обе параболы. Заштрихованная часть плоскости является фигурой, площадь которой надо найти. Для определения абсцисс точек пересечения парабол решим уравнение x2 - 2x = -2x2 + x или 3x2 - 3x = 0, откуда x1 = 0; x2 = 1.
Площадь фигуры вычисляем по формуле
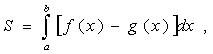 где f(x) ≥
g(x) для всех
где f(x) ≥
g(x) для всех 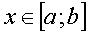
(см. [1], стр. 303, формула 11.21).В нашем случае a = x1 = 0; b = x2 = 1. На отрезке [0; 1] имеем -2x2 + x ≥ x2 - 2x. Поэтому
f(x) = -2x2 + x и g(x) = x2 - 2 x.Следовательно,
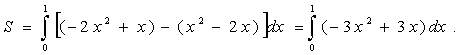
Для вычисления определенного интеграла применяется формула Ньютона-Лейбница:
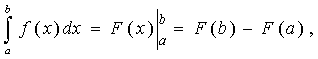
где F(x) - первообразная подынтегральной функции f(x).
Окончательно
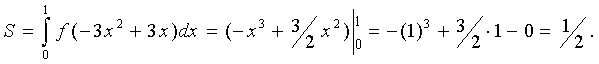
Вопросы для самопроверки:
- Что называется определенным интегралом от данной функции? Каков его геометрический смысл?
- Как связаны между собой понятия определенного и неопределенного интеграла?
- Сформулируйте теорему о производной определенного интеграла с переменным верхним пределом.
- Перечислите основные свойства определенного интеграла.
- Дайте определение несобственных интегралов с бесконечным пределом интегрирования.
Задачи 81 - 100
Вычислить площадь фигуры, ограниченной линиями y = ax2 + bx и y = cx2 + dx.
| Номер | a | b | c | d |
|---|---|---|---|---|
| 81 | 1 | -1 | -1 | 3 |
| 82 | 2 | 1 | -1 | 7 |
| 83 | -1 | -5 | 1 | 1 |
| 84 | 1/2 | 1 | -1 | 4 |
| 85 | -1 | 1 | 1/2 | -2 |
| 86 | -2 | 4 | 1/2 | -1 |
| 87 | -1 | 2 | 2 | -4 |
| 88 | 1 | -4 | -2 | 2 |
| 89 | -1/2 | 2 | 1 | -1 |
| 90 | 2 | -2 | -1/2 | 3 |
| 91 | 1 | 1 | -1 | 5 |
| 92 | -1 | 4 | 3 | -4 |
| 93 | 3 | -3 | -1 | 5 |
| 94 | 1/2 | 1 | -3 | 8 |
| 95 | -2 | 3 | 1 | -3 |
| 96 | 1 | -1 | -2 | 5 |
| 97 | -3 | 6 | 1 | -2 |
| 98 | 3 | -5 | -1/2 | 2 |
| 99 | 3 | -6 | -2 | 4 |
| 100 | -2 | -7 | 3 | -3 |
Задача 6
Найдите решение дифференциального уравнения y'' + 4y' + 3y = e-2x, удовлетворяющее начальным условиям y(0), y'(0) = 0.
Решение:
В соответствии с § 12.8 (см. [1]) общее решение данного неоднородного линейного уравнения есть сумма его частного решения и общего решения соответствующего ему линейного однородного дифференциального уравнения y'' + 4y' + 3y = 0.
Ищем общее решение однородного уравнения. В соответствии с теоремой 2.1 (см. [1], стр. 344) это решение записывается в виде
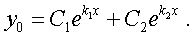
где C1 и C2 - произвольные постоянные, а k1 и k2 - корни характеристического уравнения ak2 + bk + c = 0 данного уравнения ay'' + by' + cy = 0. В нашем случае a = 1, b = 4, c = 3, характеристическое уравнение принимает вид: k2 + 4k + 3 = 0, его корни k1 = -3, k2 = -1, значит, общее решение однородного уравнения имеет вид: y0 = C1e-3x + C2e-x.
Найдем частное решение неоднородного уравнения. Согласно теореме
на стр. 342 (см. [1]), поскольку правая часть данного уравнения содержит
в показателе степени коэффициент (-2), не являющийся корнем характеристического
уравнения, частное решение следует искать в виде: y1 =
de-2x. Найдем неизвестный коэффициент d.
Так как 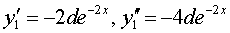 , подставив значения
, подставив значения
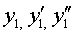 в данное уравнение, получим равенство
в данное уравнение, получим равенство
4de-2x - 8de-2x + 3de-2x = e-2xоткуда -de-2x = e-2x, т.е. d = -1.
Таким образом, общее решение данного дифференциального уравнения имеет вид
y = y0 + y1 = C1e-3x + C2e-x - e-2x.
Найдем то решение, которое удовлетворяет данным начальным условиям. Так как y' = -3C1e-3x - C2e-x +2e-2x, y(0) = C1 + C2 -1, y'(0) = -3C1 - C2 + 2, то решая систему уравнений: C1 + C2 - 1 = 2; -3C1 - C2 = 0, находим C1 = -0,5; C2 = 3,5.
Следовательно, y = -0,5e-3x + 3,5e-x - e-2x - искомое решение.
Вопросы для самопроверки:
- Дайте определение дифференциального уравнения и основных понятий, связанных с ними (порядок решения, общее решение, частное решение и интегральная кривая).
- Как можно геометрически истолковать общее и частное решения?
- Изложите методы решения типов дифференциальных уравнений первого порядка (с разделяющимися переменными, линейных).
- Изложите метод решения неоднородного уравнения второго порядка с постоянными коэффициентами.
Задачи 101 - 120
Найдите решение дифференциального уравнения ay'' + by' + cy = ekx, удовлетворяющее начальным условиям: y(0) = p, y'(0) = q.
| Номер | a | b | c | k | p | q |
|---|---|---|---|---|---|---|
| 101 | 6 | 1 | -1 | 2 | 3 | 2 |
| 102 | 10 | 7 | 1 | 0.5 | 1 | 1 |
| 103 | 4 | 8 | 3 | 3 | 0 | 5 |
| 104 | 1 | 7 | 6 | 5 | 3 | 1 |
| 105 | 1 | 5 | 4 | 1 | 1 | 2 |
| 106 | 3 | 5 | 2 | 4 | 3 | 8 |
| 107 | 4 | 7 | 3 | 1 | 2 | 2 |
| 108 | 8 | 9 | 1 | 3 | 3 | 5 |
| 109 | 2 | 5 | 3 | 8 | 6 | 2 |
| 110 | 4 | 9 | 5 | 4 | 9 | 2 |
| 111 | 6 | 11 | 5 | 3 | 2 | 1 |
| 112 | 3 | 7 | 4 | 3 | 0 | 3 |
| 113 | 5 | 8 | 3 | 2 | 4 | 2 |
| 114 | 6 | 13 | 7 | 3 | 4 | 2 |
| 115 | 2 | 9 | 7 | 5 | 4 | 2 |
| 116 | 4 | 11 | 7 | 4 | 0 | 3 |
| 117 | 7 | 8 | 1 | 4 | 5 | 2 |
| 118 | 8 | 13 | 5 | 3 | 1 | 0 |
| 119 | 5 | 9 | 4 | 3 | 1 | 4 |
| 120 | 3 | 7 | 4 | 2 | 3 | 2 |