Тема 1. Оптимизационные экономико-математические модели
Тема 2. Методы получения оптимальных решений
Тема 4. Методы и модели анализа экономических процессов
Тема 5. Прогнозирование экономических процессов с использованием временных рядов
Тема 6. Производственные функции
Тема 7. Методы и модели управления и принятия решений в экономических системах
Тема 2. Методы получения оптимальных решений
2.1. Основы линейного программирования. Математический аппарат линейного программирования. Различные формы записи задачи линейного программирования (ЗЛП). Графическое решение задачи линейного программирования, исследование случаев неразрешимости задачи. Основы симплекс-метода, процедуры решения с естественным и искусственным базисом. Особые случаи решения ЗЛП. Двойственность в линейном программировании, свойства двойственных оценок и их использование в анализе оптимального плана.
2.2. Специальные задачи линейного программирования. Экономико-математическая модель транспортной задачи, ее модификации. Модели целочисленного линейного программирования (задачи о назначениях, инвестициях и т.п.). Общие сведения о методах реализации.
2.3. Основные понятия и общие сведения о методах реализации моделей нелинейного и динамического программирования.
Для изучения оптимизационных моделей необходимо повторение ряда разделов курса высшей математики:
— матрицы, действия над матрицами;
— обратная матрица, ее вычисление;
— ранг матрицы и его вычисление;
— определители, их свойства, вычисление определителей;
— миноры и алгебраические дополнения, их вычисление;
— системы линейных уравнений, решение методом обратной матрицы;
— исследование систем линейных уравнений методом Жордана-Гаусса;
— векторы и простейшие действия над ними;
— линейная зависимость и независимость системы векторов, базис системы векторов;
— линейные векторные пространства, базис пространства, естественный базис, переход от одного базиса к другому;
— выпуклые множества, выпуклые и вогнутые функции.
Необходимый минимум материала по указанным вопросам содержится в учебном пособии [1, с. 30-49]. Эти сведения являются частью базовых математических знаний, составляющих необходимую математическую культуру современного экономиста.
После повторения указанного материала следует перейти к изучению дальнейшего материала.
Рассмотрим последовательно основные вопросы по приведенным выше разделам темы 2.
2.1. Основы линейного программирования
В наиболее общем виде задача (модель) линейного программирования записывается следующим образом: требуется найти максимум (или минимум) линейной целевой функции
f(x1, x2,…, xn) = c1x1 + c2x2 + … +cnxn (2.1)
при ограничениях
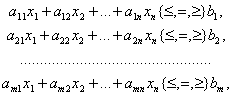 (2.2)
(2.2)
xj ≥ 0, j = 1, 2, …, n, (2.3)
где — aij, bi, cj (i = 1, 2, ... m, j = 1, 2,..., n) — заданные постоянные величины.
Это развернутая форма записи общей задачи линейного программирования (ЗЛП); знак {≤, =, ≥} означает, что в конкретной ЗЛП возможно ограничение типа равенства или неравенства (со знаком в ту или иную сторону).
Систему ограничений (2.2) называют функциональными ограничениями ЗЛП, а ограничения (2.3) - прямыми.
Вектор Х = (x1, x2, …, xn), удовлетворяющий системе ограничений (2.2) и (2.3), называется допустимым решением или планом ЗЛП, т. е. ограничения (2.2), (2.3) определяют область допустимых решений или планов ЗЛП (область определения ЗЛП).
План (допустимое решение), который доставляет максимум или минимум целевой функции (2.1), называется оптимальным планом (оптимальным решением) ЗЛП.
Канонической формой записи ЗЛП (КЗЛП) называют задачу вида (запись с использованием знаков суммирования)
max (min) f(x1, x2, …, xn) = ∑cjxj
найти при ограничениях
∑aijxj = bi, i = 1, 2, …, m,
xj ≥ 0, j = 1, 2, …, n; bi ≥ 0, i = 1, 2, …, m.
Векторная форма записи КЗЛП имеет вид:
max (min) f(x1, x2, …, xn) = f(X) = CX
A1x1 + A2x2 + … + Anxn = B,
X ≥ 0
где: C = (c1, c2, …, cn), X = (x1, x2, …, xn);
СХ - скалярное произведение векторов С и X;
A1, A2, …, An - вектор-столбцы.
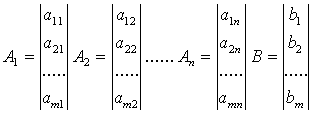
Запись X ≥ 0 означает, что все компоненты вектора X неотрицательны.
Матричная форма записи КЗЛП имеет вид:
max (min) f(X) = CX,
АХ = В,
Х ≥ 0.
где C = (c1, c2, …, cn) - матрица-строка;
Х - матрица-столбец;
B - матрица-столбец;
A = (aij) — матрица размерности m × n, столбцами которой являются вектор-столбцы A1, A2, …, An.
Иногда используется стандартная форма записи ЗЛП:
max (min) f(X)= CX,
АХ ≤ (≥) В,
Х ≥ 0.
При этом запись вектор АХ меньше или равен (больше или равен) вектору В понимается так, что все компоненты вектора слева меньше или равны (больше или равны) соответствующим компонентам вектора справа.
Имеет место утверждение, что любую ЗЛП можно привести к каноническому виду.
Приведение ЗЛП к каноническому виду осуществляется введением в левую часть соответствующего ограничения вида (2.2) k-й дополнительной (вспомогательной) переменной xn+k ≥ 0 со знаком «—» в случае ограничения типа «≥» и знаком «+» в случае ограничения типа «≤».
Если на некоторую переменную xp не
накладывается условие неотрицательности, то делают замену переменных
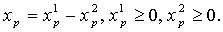 В преобразованной задаче все переменные
неотрицательные.
В преобразованной задаче все переменные
неотрицательные.
Пример 1. Привести к каноническому виду следующую ЗЛП:
max f(x1, x2) = (x1 + 2x2)
2x1 + 3x2 ≤ 10
2x1 + x2 = 6
x1 + x2 ≥ 2
x1,2 ≥ 0.
Сделаем замену переменных 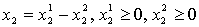 ;
введем в левую часть первого ограничения дополнительную переменную х3
≥ 0 (со знаком «+») и в левую часть третьего ограничения дополнительную
переменную х4 ≥ 0 (со знаком «-»). Будем иметь КЗЛП:
;
введем в левую часть первого ограничения дополнительную переменную х3
≥ 0 (со знаком «+») и в левую часть третьего ограничения дополнительную
переменную х4 ≥ 0 (со знаком «-»). Будем иметь КЗЛП:
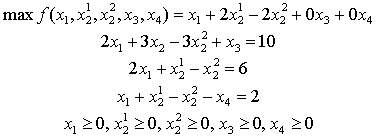
Любая ЗЛП может быть приведена к стандартной форме (как добиться неотрицательности всех переменных показано выше), а ограничение типа равенства следует заменить на два ограничения типа неравенств со «встречными» знаками неравенств (одно неравенство типа «≤», другое - типа «≥»). Рассмотрим ЗЛП в стандартной форме записи:
max f(x1, x2, …, xn) = ∑cjxj, (2.4)
∑aijxj ≤ bj, i = 1, 2, …, m, (2.5)
xj ≥ 0, j = 1, 2, …, n. (2.6)
Положим n = 2, т.е. рассмотрим эту задачу на плоскости. Пусть система неравенств (2.5), (2.6) совместна (имеет хотя бы одно решение):
a11x1 + a12x2 ≤ b1
a21x1 + a22x2 ≤ b2
am1x1 + am2x2 ≤ bm
x1,2 ≥ 0.
Каждое неравенство этой системы геометрически определяет полуплоскость с граничной прямой ai1x1 + ai2x2 = bi, i = 1, 2, …, m. Условия неотрицательности определяют полуплоскости с граничными прямыми х1 = 0, х2 = 0 соответственно. Система совместна, поэтому полуплоскости как выпуклые множества, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты каждой из которых являются решением данной системы [1]. Совокупность этих точек называют многоугольником решений. Он может быть точкой, отрезком, лучом, многоугольником, неограниченной многоугольной областью.
Если в системе ограничений (2.5), (2.6) n = 3, то каждое неравенство геометрически представляет полупространство трехмерного пространства, граничная плоскость которого ai1x1 + ai2x2 + ai3x3 = bi, i = 1, 2, ..., m, а условия неотрицательности -полупространства с граничными плоскостями хj = 0, j = 1, 2, 3, соответственно. Если система ограничений совместна, то эти полупространства как выпуклые множества, пересекаясь, образуют в трехмерном пространстве общую часть, которая называется многогранником решений.
Пусть в системе ограничений (2.5), (2.6) n > 3, тогда каждое неравенство определяет полупространство n-мерного пространства с граничной гиперплоскостью ∑aij, xj = bi, i = 1, 2, …, m, а условия неотрицательности - полупространства с граничными гиперплоскостями хj = 0, j = 1, 2, ..., n. Если система ограничений совместна, то по аналогии с трехмерным пространством она образует общую часть n-мерного пространства, называемую многогранником решений, т.к. координаты каждой его точки являются решением.
Таким образом, геометрически задача линейного программирования представляет собой отыскание такой точки многогранника решений, координаты которой доставляют линейной функции цели максимальное (минимальное) значение, причем допустимыми решениями являются все точки многогранника решений.
Если целевая функция (ЦФ) ЗЛП ограничена на многограннике решений (на плоскости — многоугольнике решений), то:
- существует такая угловая (крайняя) точка многогранника решений, в которой ЦФ достигает своего оптимума;
- каждый опорный план ЗЛП соответствует угловой точке многогранника решений.
Для решения ЗЛП необходимо исследовать только вершины (угловые точки) многогранника решений - области допустимых решений (ОДР), т.е. только опорные планы.
ЗЛП не имеет решения в случаях, когда:
- ОДР — пустое множество, т.е. при несовместности системы ограничений,
- ОДР представляет собой неограниченную многогранную область, при этом ЦФ не ограничена сверху (при максимизации) или снизу (при минимизации). Обычно эти случаи связаны с некорректностями в экономической постановке задачи или в ее математическом описании (модели).
Если в ЗЛП ограничения заданы в виде неравенств, с двумя переменными, то она может быть решена графически. Графический метод решения ЗЛП состоит из следующих этапов.
1. Строится многоугольная область допустимых решений ЗЛП - ОДР.
2. Строится вектор-градиент ЦФ в какой-нибудь точке X0 принадлежащей ОДР - ∇ = (С1, С2).
3. Линия уровня С1x1 + С2x2 = а (а — постоянная величина) - прямая, перпендикулярная вектору-градиенту ∇ - передвигается в направлении этого вектора в случае максимизации f(x1, x2) до тех пор, пока не покинет пределов ОДР. Предельная точка (или точки) области при этом движении и является точкой максимума f(x1, х2).
4. Для нахождения ее координат достаточно решить два уравнения прямых, получаемых из соответствующих ограничений и дающих в пересечении точку максимума. Значение f(x1, x2), найденное в получаемой точке, является максимальным.
При минимизации f(x1, x2) линия уровня перемещается в направлении, противоположном вектору-градиенту. Если прямая при своем движении не покидает ОДР, то соответствующий максимум или минимум f(x1, x2) не существует.
Если линия уровня параллельна какому-либо функциональному ограничению задачи, то оптимальное значение ЦФ будет достигаться в любой точке этого ограничения, лежащей между двумя оптимальными угловыми точками, и соответственно любая из этих точек является оптимальным решением ЗЛП.
Пример 2. Решить графическим методом следующую ЗЛП:
f(x1, x2) = (5x1 + 4x2) → max, min
2x1 + 5x2 ≤ 20
8x1 + 5x2 ≤ 20
5x1 + 6x2 ≤ 30
x1,2 ≥ 0
1. Построим ОДР задачи (рис. 2.1).
Прямые ограничения означают, что область решений будет лежать в первой четверти Декартовой системы координат.
Функциональные ограничения (неравенства) определяют область, являющуюся пересечением нижних полуплоскостей с граничными прямыми:
2x1 + 5х2 = 20
8x1 + 5x2 = 40
5х1 + 6х2 = 30.
Пересечение указанных полуплоскостей в первой четверти представляет собой многоугольник OABCD (заштрихованная общая область для всех ограничений задачи ОДР).
2. Для определения направления движения к оптимуму построим вектор-градиент, соединив его вершину ∇(5, 4) с началом координат О (0, 0).
3. Построим некоторую линию уровня 5x1 + 4x2 = а.
Пусть, например, а = 0. На рис. 2.1 такой линии уровня отвечает прямая ОХ, перпендикулярная вектор-градиенту.
4. При максимизации ЦФ необходимо перемещать линию уровня ОХ в направлении вектор-градиента, а при минимизации — в противоположном направлении. Предельными точками при таком движении линии уровня ОХ являются соответственно точка С и точка О. Далее она выходит из ОДР.
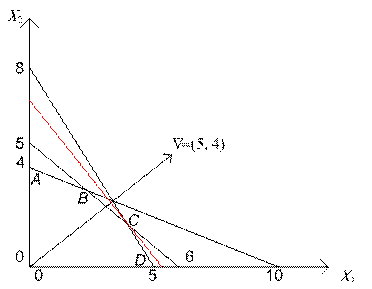
Рис. 2.1
Определим координаты точки С, являющейся точкой пересечения второй и третьей прямых:
8x1 + 5x2 = 40,
5x1 + 6x2 = 30,
x1 ≈ 3,9; x2 ≈ 1,7.
Таким образом, ЦФ в ЗЛП принимает при х1 ≈ 3,9; x2 ≈ 1,7 максимальное значение, равное
f(x1, х2) = 5 × 3,9 + 4 × 1,7 ≈ 26,3.
Поскольку координаты точки О равны х1 = 0; x2 = 0, то минимум ЦФ равен 0.
Указанные выше два случая отсутствия решений в ЗЛП иллюстрируются рисунками 2.2 и 2.3, на которых графически представлены задачи:
| 1) max f(x1, x2) = (3x1 + 5x2) | 2) max f(x1, x2) = (3x1 + 2x2) |
| x1 + x2 ≥ 2 | x1 - x2 ≤ 1 |
| 4x1 + 2x2 ≤ 2 | 2x1 + x2 ≥ 1 |
| x1,2 ≥ 0 | x1,2 ≥ 0 |
Как видно из рисунков, первая из приведенных ЗЛП не имеет решения, поскольку ее множество допустимых решений - пустое множество, вторая — поскольку не существует конечного максимума на неограниченном множестве допустимых решений.
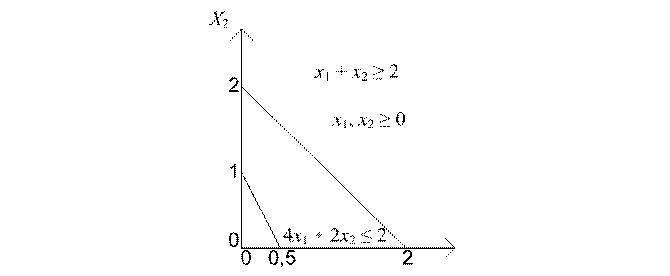
Рис. 2.2
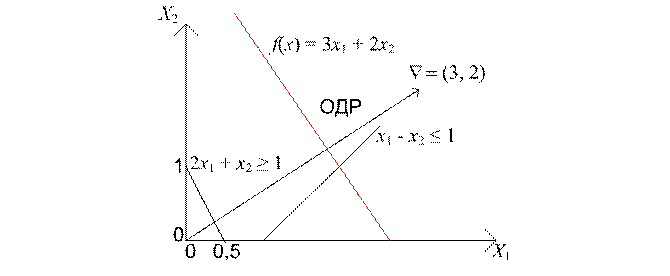
Рис. 2.3
Случай неединственности решения иллюстрируется следующей задачей:
max f(х1, х2) = (8х1 + 10x2)
5х1 + х2 ≤ 15
4х1 + 5х2 ≤ 40
x2 ≥ 3
х1 ≥ 0.
Графическое решение этой задачи показано на рис. 2.4.
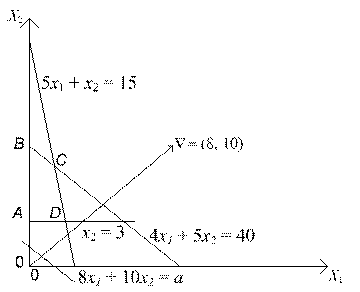
Рис. 2.4
Линия уровня 8х1 + 10х2 = а параллельна одной из линий по границе области допустимых решений (4х1 + 5х2 = 40).
Это означает, что задача имеет бесконечное множество оптимальных решений (его задают координаты точек отрезка ВС), среди которых опорных оптимальных решений два соответственно в угловых точках В (0, 8) и С (5/3, 20/3).
Точки отрезка ВС задаются уравнением х2 = 8 - 0,8х1, где 0 ≤ х1 ≤ 5/3. При этом максимальное значение целевой функции равно 80.
В общем случае, если оптимальными решениями являются опорные решения Х1 и Х2, то все множество оптимальных решений (отрезок, соединяющий две соответствующие соседние угловые точки) определяется выражением Х = αХ1 + (1 - α)Х2, где 0 ≤ α ≤ 1.
Перейдем к рассмотрению аналитического метода решения задач линейного программирования.
Для решения ЗЛП существует универсальный метод — метод последовательного улучшения плана или симплекс-метод, который состоит из двух вычислительных процедур: симплекс-метода с естественным базисом и симплекс-метода с искусственным базисом.
Выбор конкретной вычислительной процедуры осуществляется после приведения исходной ЗЛП к каноническому виду (КЗЛП):
max f(x1, x2, …, xn) = ∑cjxj,
Saij = bi, i = 1, 2, …, m,
xj ≥ 0, j = 1, 2, …, n; bi ≥ 0, i = 1, 2, …, m.
В теории линейного программирования (ЛП) показано, что оптимальное
решение ЗЛП связано с угловыми (крайними) точками многогранника решений,
которым отвечают опорные планы (неотрицательные базисные решения системы
уравнений КЗЛП). Каждый из опорных планов определяется системой m
линейно независимых векторов, содержащихся в данной системе из n
векторов A1, A2, ..., Аn
Верхняя граница количества опорных планов, содержащихся в данной задаче,
определяется числом сочетаний 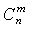 .
.
Пример 3. Решить ЗЛП по модели задачи об оптимальном использовании ограниченных ресурсов:
max f(x1, x2) = (2x1 + 3x2)
х1 + 3х2 ≤ 300
x1 + х2 ≤ 150
х1,2 ≥ 0.
Приведем задачу к каноническому виду путем введения дополнительных переменных х3 и х4:
max (2х1 + 3х2 + 0х3 + 0х4)
x1 + 3x2 + x3 = 300
x1 + x2 + x4 = 150
x1,2,3,4 ≥ 0.
Найдем все опорные планы КЗЛП. Используя метод Жордана-Гаусса [1] выписываем все базисные решения системы уравнений:
х1 + 3x2 + x3 = 300
x1 + x2 + x4 = 150.
Последовательно будем иметь:
X1 = (0, 0, 300, 150); Х2 = (150, 0, -150, 0); Х3 = (0, 150, -150, 0); X4 = (75, 75, 0, 0); X5 = (300, 0, 0, -150); Х6 = (0, 100, 0, 50).
Среди этих базисных решений четыре опорных:
X1 = (0, 0, 300, 150); Х2 = (150, 0, 150, 0); Х4 = (75, 75, 0, 0); Х6 = (0, 100, 0, 50).
Указанным опорным планам на рис. 2.5 отвечают соответственно следующие угловые точки и значения ЦФ в них:
А (0, 0) и f (0, 0) = 0;D (150, 0) и f (150, 0) = 300; С (75, 75) и f (75, 75) = 375; В (0, 100) и f (0, 100) = 300.
Согласно теории ЛП оптимальное решение содержится среди опорных планов.
Таким образом, максимальное значение, равное 375, целевая функция f(x1, х2) достигает на опорном плане Х4 = (75, 75, 0, 0), т.е. оптимальное решение рассматриваемой ЗЛП: х1 = 75, x2 = 75.
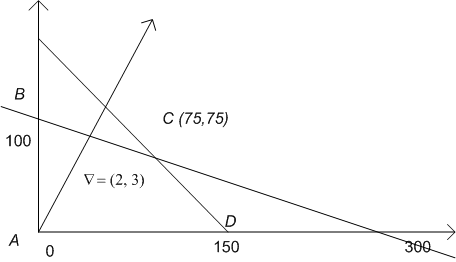
Рис. 2.5
Понятно, что при больших m и n найти оптимальный план, перебирая указанным выше способом (прямым перебором) все опорные ЗЛП весьма трудно. Поэтому необходимо иметь схему, позволяющую осуществлять упорядоченный переход от одного опорного плана к другому. Такой схемой является симплексный метод, идея которого изложена в [1].
Для применения симплекс-метода с естественным базисом КЗЛП должна содержать единичную подматрицу размером m × m: в этом случае очевиден начальный опорный план (неотрицательное базисное решение системы ограничений КЗЛП).
Для определенности предположим, что первые m векторов матрицы системы уравнений составляют единичную матрицу. Тогда первоначальный опорный план очевиден — (b1, b2, …, bm, 0, …, 0).
Проверка на оптимальность опорного плана проходит с помощью признака оптимальности, переход к другому опорному плану проводится с помощью преобразований Жордана—Гаусса при использовании математического признака оптимальности. Полученный опорный план снова проверяется на оптимальность и т.д. Процесс заканчивается за конечное число шагов, причем на последнем шаге либо выявляется неразрешимость задачи (конечного оптимума нет), либо получается оптимальный опорный план и соответствующее ему оптимальное значение ЦФ.
Математический признак оптимальности состоит из следующих двух теорем.
1. Если для всех векторов А1, А2, ..., Аn выполняется условие Δj = Zj – cj ≥ 0, где Zj = ∑cj × aij, то полученный опорный план является оптимальным.
2. Если для некоторого вектора, не входящего в базис, выполняется условие Δj = Zj - cj < 0, то можно получить новый опорный план, для которого значение ЦФ будет больше исходного, при этом могут быть два случая:
- если все компоненты вектора, подлежащего вводу в базис, неположительны, то ЗЛП не имеет решения (конечного оптимума нет);
- если имеется хотя бы одна положительная компонента у вектора, подлежащего вводу в базис, то можно получить новый опорный план.
На основании признака оптимальности в базис вводится вектор Аk, давший минимальную отрицательную величину симплекс-разности:
Δk = min (Zj- сj), j = 1, 2, ..., n.
Чтобы выполнялось условие неотрицательности значений опорного плана, выводится из базиса вектор Аr который дает минимальное положительное оценочное отношение
Q = min (bi/aik) = br/ark, aik > 0, i = 1, 2, ..., m.
Строка Аr называется направляющей, столбец Аk и элемент ark - направляющими.
Элементы направляющей строки в новой симплекс-таблице вычисляются по формулам:
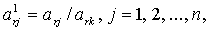
а элементы i-и строки - по формулам:
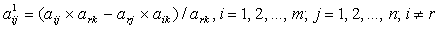
Значения нового опорного плана рассчитываются по формулам:
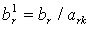 для i = r;
для i = r;
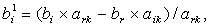 i = 1, 2, …, m; i
≠ r.
i = 1, 2, …, m; i
≠ r.
Процесс решения продолжают либо до получения оптимального плана, либо до установления неограниченности ЦФ. Если среди симплекс-разностей (оценок) оптимального плана нулевые только оценки, соответствующие базисным векторам, то это говорит о единственности оптимального плана. Если же нулевая оценка соответствует вектору, не входящему в базис, то в общем случае это означает, что оптимальный план не единственный.
Примечание. Для использования приведенной процедуры к минимизации линейной функции f(x1, x2, …, xn) следует искать максимум — f(x1, x2, …, xn), затем полученный максимум взять с противоположным знаком. Оптимальное решение то же.
Пример. Решить ЗЛП по модели:
max (2х1 + 3x2)
х1 + 3х2 ≤ 300
х1 + x2 ≤ 150
x1,2 ≥ 0.
Эту ЗЛП приведем к каноническому виду путем введения дополнительных переменных х3 и x4:
max (2х1 + 3x2+ 0x3 + 0x4)
x1 + 3x2 + х3 = 300
х1 +x2 + х4= 150
x1,2,3,4 ≥ 0.
КЗЛП имеет необходимое число единичных столбцов, т.е. обладает очевидным начальным опорным планом (0, 0, 300, 150). Решение осуществляется симплекс-методом с естественным базисом с оформлением расчетов в симплекс-таблицах:
| Номер симплекс-таблицы | Базис | Cj | B | 2 | 3 | 0 | 0 | Q |
|---|---|---|---|---|---|---|---|---|
| Ci | А1 | А2 | A3 | А4 | ||||
| 0 | A3 | 0 | 300 | 1 | 3 | 1 | 0 | 100 |
| A4 | 0 | 150 | 1 | 1 | 0 | 1 | 150 | |
| ∆φ | - | 0 | -2 | -3 | 0 | 0 | - | |
| I | A2 | 3 | 100 | 1/3 | 1 | 1/3 | 0 | 300 |
| A4 | 0 | 50 | 2/3 | 0 | -1/3 | 1 | 75 | |
| ∆ | - | 300 | -1 | 0 | 1 | 0 | - | |
| II | A2 | 3 | 75 | 0 | 1 | 1/2 | -1/2 | - |
| A1 | 2 | 75 | 1 | 0 | -1/2 | 3/2 | - | |
| ∆ | - | 375 | 0 | 0 | 1/2 | 3/2 | - |
В симплекс-таблице II получен оптимальный опорный план, поскольку
все симплекс-разности (оценки) ∆j ≥ 0, j
= 1, 2, 3, 4. Оптимальные значения переменных равны:
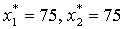 (основные переменные),
(основные переменные),
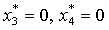 (дополнительные переменные). Максимальное
значение целевой функции равно 375.
(дополнительные переменные). Максимальное
значение целевой функции равно 375.
Таким образом, в рассмотренной выше задаче об оптимальном использовании ограниченных ресурсов оптимальная производственная программа состоит в выпуске 75 ед. изделий первого вида и 75 ед. изделий второго вида. С этой программой связана максимальная выручка от реализации готовой продукции — 375 у.е.
В ходе использования рассматриваемой процедуры может быть установлен факт неразрешимости ЗЛП вследствие отсутствия конечного оптимума (все компоненты вектора, подлежащего вводу в базис неположительны).
Пример 4. Решить ЗЛП по модели:
max (-3x1 - 2x2 + 2x3)
-x1 - x2 - x3 + x4 = 1
-2x1 - x2 + x3 + x5 = 1
x1,2,3,4,5 ≥ 0
Решение этой КЗЛП осуществляется симплекс-методом с естественным базисом с оформлением расчетов в симплекс-таблицах:
| Номер симплекс-таблицы | Базис | Cj | B | -3 | -2 | 2 | 0 | 0 | Q |
|---|---|---|---|---|---|---|---|---|---|
| Ci | А1 | А2 | A3 | А4 | А5 | ||||
| 0 | A4 | 0 | 1 | -1 | -1 | -1 | 1 | 0 | - |
| A5 | 0 | 1 | -2 | -1 | 1 | 0 | 1 | 1 | |
| ∆φ | - | 0 | 3 | 2 | -2 | 0 | 0 | - | |
| I | A4 | 0 | 2 | -3 | -2 | 0 | 1 | 1 | - |
| A3 | 2 | 1 | -2 | -1 | 1 | 0 | 1 | - | |
| ∆ | - | 2 | -1 | 0 | 0 | 0 | 2 | - |
В симплекс-таблице I все компоненты вектора А1, подлежащего вводу в базис, отрицательны. Задача не имеет решения вследствие неограниченности сверху целевой функции.
Симплекс-метод с искусственным базисом (М-метод) применяется в тех случаях, когда затруднительно найти первоначальный опорный план канонической формы задачи ЛП.
Этот метод заключается в применении правил симплекс-метода к так называемой М-задаче. Она получается из исходной добавлением к левой части векторного уравнения таких искусственных единичных векторов с соответствующими неотрицательными искусственными переменными, чтобы вновь полученная матрица содержала систему единичных, линейно-независимых векторов. В линейную форму исходной задачи добавляется в случае ее максимизации слагаемое, представляющее собой произведение числа (-М) на сумму искусственных переменных, где М - достаточно большое число.
В полученной задаче первоначальный опорный план очевиден. При применении к этой задаче симплекс-метода оценки ∆j теперь будет зависеть «от буквы М». Для сравнения оценок нужно помнить, что М — достаточно большое число.
В процессе решения М-задачи следует вычеркивать в симплекс-таблице искусственные векторы по мере их выхода из базиса. Если все искусственные векторы вышли из базиса, то получаем исходную задачу. Если в оптимальном решении М-задачи хотя бы одна из искусственных переменных отлична от нуля, то система ограничений исходной задачи несовместна (задача неразрешима). В случае неразрешимости М-задачи будет неразрешима и исходная задача (либо максимум бесконечен, либо условия задачи противоречивы).
Пример 5. Решить ЗЛП по модели:
min f(X) = 10x1 – 5x2
2x1 – х2 ≥ 3
х1 + х2 ≥ 2
х1 + 2х2 ≥ -1
х1,2 ≥ 0.
Эту ЗЛП приведем к каноническому виду и одновременно перейдем к задаче «на максимум»:
max (-10х1 + 5x2)
2х1 - х2 – х3 = 3
x1 + x2 - x4 = 2
x1 - 2x2 + х5 = 1
x1,2,3,4,5 ≥ 0.
Для нахождения опорного плана переходим к М-задаче:
max (-10х1 + 5х2 – My1 - My2)
2x1 - x2 - x3 + y1 = 3
х1 + x2 – х4 + у2 = 2
-х1 - 2х2 + х5 = 1
x1,2,3,4,5 ≥ 0, y1, y2 ≥ 0.
Дальнейшее решение проводим в симплекс-таблицах:
В симплекс-таблице II получен опорный план исходной ЗЛП. Поскольку
все симплекс-разности ∆j ≥ 0, j = 1, 2,
3, 4, 5, то этот план является и оптимальным, т.е.
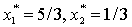 (основные переменные),
(основные переменные),
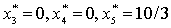 (дополнительные переменные), f(X*)
= 15 (исходная задача на минимум).
(дополнительные переменные), f(X*)
= 15 (исходная задача на минимум).
| Номер симплекс-таблицы | Базис | Cj | B | -10 | 5 | 0 | 0 | 0 | -M | -M | Q |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ci | А1 | А2 | A3 | А4 | A5 | P1 | P2 | ||||
| 0 | P1 | -M | 3 | 2 | -1 | -1 | 0 | 0 | 1 | 0 | 3/2 |
| P2 | -M | 2 | 1 | 1 | 0 | -1 | 0 | 0 | 1 | 2 | |
| A5 | 0 | 1 | -1 | -2 | 0 | 0 | 1 | 0 | 0 | - | |
| ∆φ | - | -5M | -3M+10 | -5 | M | M | 0 | 0 | 0 | - | |
| I | A1 | -10 | 3/2 | 1 | -1/2 | -1/2 | 0 | 0 | 0 | - | |
| P2 | -M | 1/2 | 0 | 3/2 | 1/2 | -1 | 0 | 1 | 1/3 | ||
| A5 | 0 | 5/2 | 0 | -5/2 | -1/2 | 0 | 1 | 0 | - | ||
| ∆ | - | -M/2-15 | 0 | -3M/2 | -M/2+5 | M | 0 | 0 | - | ||
| II | A1 | -10 | 5/3 | 1 | 0 | -1/3 | -1/3 | 0 | |||
| A2 | 5 | 1/3 | 0 | 1 | 1/3 | -2/3 | 0 | ||||
| A5 | 0 | 10/3 | 0 | 0 | 0 | -5/3 | 1 | ||||
| ∆ | - | -15 | 0 | 0 | 5 | 0 | 0 | - |
Особый случай симплексного метода - случай неединственности оптимального решения — иллюстрирует следующий пример.
Пример 6. Решить ЗЛП по модели:
max ( -15х1)
3х1 - 2х2 ≤ 10
х1 + 2х2 ≤ 5
x1,2 ≥ 0.
Приводим эту задачу к каноническому виду и решаем симплекс-методом с естественным базисом с оформлением расчетов в симплекс-таблицах:
| Номер симплекс-таблицы | Базис | Cj | B | -15 | 0 | 0 | 0 | Q |
|---|---|---|---|---|---|---|---|---|
| Ci | А1 | А2 | A3 | А4 | ||||
| 0 | A3 | 0 | 10 | 3 | -2 | 1 | 0 | - |
| A4 | 0 | 5 | 1 | 2 | 0 | 1 | 2,5 | |
| ∆φ | - | 0 | 15 | 0 | 0 | 0 | - | |
| I | A3 | 0 | 15 | 4 | 0 | 1 | 1 | |
| A2 | 0 | 2,5 | 0,5 | 1 | 0 | 0,5 | ||
| ∆ | - | 0 | 15 | 0 | 0 | 0 | - |
В симплекс-таблице 0 все оценки ∆j ≥ 0, j = 1, 2, 3, 4, т.е. план х1 = (0; 0; 10; 5) является оптимальным. Кроме того, это решение не является единственным, поскольку для внебазисной переменной х2 оценка ∆2 = 0. Перейдем к следующему опорному плану: для этого введем в число базисных вектор А2, а вектор A4 исключим из базиса. Получим в симплекс-таблице I новый опорный план х2 = (0; 2,5; 15; 0), который также является оптимальным (∆j ≥ 0, j = 1, 2, 3, 4); т.е. целевая функция достигает максимума в двух угловых точках многогранника решений, а значит, и в любой точке, являющейся выпуклой линейной комбинацией этих угловых точек. Таким образом, в рассматриваемой задаче имеется бесконечное множество оптимальных решений, которое можно представить выражением: х = aх1 + (1 - а)х2, 0 ≤ а ≤ 1.
Примечание. Если опорный план вырожденный, т.е. среди его базисных компонент есть хотя бы одна нулевая, то минимальное оценочное отношение Q может оказаться равным нулю и значение ЦФ при переходе к новому опорному плану не изменится. В этом случае вычисления проводят аналогично рассмотренным. Теоретически возможно зацикливание (возврат к уже встречавшемуся базису), однако в практических задачах это встречается крайне редко.
Перейдем к рассмотрению специального инструментария для проведения экономико-математического анализа полученного оптимального плана - теории двойственности в линейном программировании.
При этом математические утверждения принимаются без доказательства - необходимо содержательно их понимать и уметь использовать в экономическом анализе.
С каждой задачей линейного программирования определенным образом (по определенному правилу) связана другая ЗЛП, называемая двойственной к исходной (первоначальной) задаче.
Связь исходной и двойственной задач заключается, в частности, в том, что решение одной их них может быть получено непосредственно из решения другой. Имея решение двойственной задачи, которое интерпретируется как совокупность условных оценок (теневых цен) участвующих в производстве ресурсов, можно провести экономико-математический анализ оптимального плана исходной задачи и сделать ряд экономически содержательных выводов.
Правило построения двойственной задачи определяется системой соотношений:
| Исходная задача | Двойственная задача |
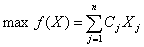 |
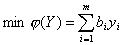 |
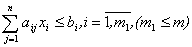 |
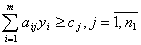 |
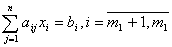 |
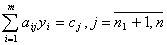 |
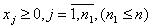 |
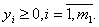 |
Пример 7. Записать двойственную задачу к следующей исходной:
max f(X) = x1 + х2 + 2х3
2х1 + х2 + х3 ≤ 15
2х2 + 3x3 ≥ 10
x1 + х2 + 4х3 = 8
x1 ≥ 0, x2 ≥ 0.
Для использования приведенного правила построения двойственной задачи умножим обе части второго неравенства на (-1). Будем иметь:
| Исходная задача | Двойственная задача |
| max f(X) = x1 + х2 + 2х3 | min φ(Y) = 15y1 - 10y2 + 8y3 |
| 2x1 + x2 + x3 ≤ 15 | 2y1 + y3 ≥ 1 |
| -2x2 - 3x3 ≤ -10 | y1 - 2y2 + y3 ≥ 1 |
| x1 + x2 + 4x3 = 8 | y1 - 3y2 + 4y3 = 2 |
| x1 ≥ 0, x2 ≥ 0. | y1 ≥ 0, y2 ≥ 0. |
В качестве исходной задачи в приведенной паре взаимно двойственных задач можно принимать и задачу на минимум. Прежде чем записать двойственную задачу для данной исходной, систему ограничений исходной задачи необходимо привести к соответствующему виду.
Пример 8. Записать двойственную задачу к исходной задаче
min f(X) = 2x1 - 3x2
2x1 – x2 ≤ -4
x1 + х2 ≥ 5
х1 ≥ 0, х2 ≥ 0.
Для использования приведенного выше правила умножим первое неравенство на -1.
| Исходная задача | Двойственная задача |
| min f(X) = 2x1 - 3x2 | max φ(Y) = (4y1 + 5y2) |
| -2x1 + x2 ≥ 4 | -2y1 + y2 ≤ 2 |
| x1 + x2 ≥ 5 | y1 + y2 ≤ -3 |
| x1 ≥ 0, x2 ≥ 0 | y1 ≥ 0, y2 ≥ 0. |
Связь между оптимальными планами пары двойственных задач устанавливают теоремы двойственности.
Теорема 1 (основная теорема двойственности). Если одна из двойственных задач разрешима, то разрешима и другая, причем экстремальные значения целевых функций задач равны: max f(X) = f(X*) = min φ(Y) = φ(Y*). Если одна из двойственных задач неразрешима, то неразрешима и другая.
Теорема 2 (о дополняющей нежесткости). Если при подстановке компонент оптимального плана в систему ограничений исходной задачи i-е ограничение обращается в неравенство, то i-я компонента оптимального плана двойственной задачи равна нулю. Если i-я компонента оптимального плана двойственной задачи положительна, то i-e ограничение исходной задачи удовлетворяется ее оптимальным решением как строгое равенство.
То есть для оптимальных планов двойственных задач имеют место соотношения:
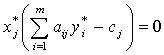
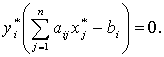
Оптимальные значения переменных двойственной задачи и называют двойственными оценками (теневыми ценами, объективно обусловленными оценками).
Пример 9. На станках трех видов С1, С2, С3 последовательно обрабатываются детали четырех видов: D1, D2, D3, D4. Известно, сколько часов каждая деталь изготавливается на каждом станке, сколько времени может отработать каждый станок и какая прибыль может быть получена при продаже одной детали каждого вида. Данные для решения задачи содержатся в таблице:
| Станки | Сколько требуется часов работы станка для выпуска одной детали, час/дет. | Фонд времени станка, час | |||
|---|---|---|---|---|---|
| D1 | D2 | D3 | D4 | ||
| С1 | 2 | 4 | 0 | 8 | 12 |
| С2 | 7 | 2 | 2 | 6 | 8 |
| С3 | 5 | 8 | 4 | 3 | 48 |
| Прибыль на одну деталь, у.е./дет. | 3 | 4 | 3 | 1 | - |
Найден оптимальный по критерию «максимум прибыли» план, предусматривающий выпуск трех деталей второго вида и одной детали третьего вида. Дать экономико-математический анализ оптимального плана.
Решение.
Обозначим через хj = 1,4 - объем выпуска деталей j-го вида и запишем математическую модель задачи критерию «максимум прибыли»:
max (3x1 + 4x2 + 3x3 + x4)
2x1 + 4х2 + 8х4 ≤ 12
7x1 + 2х2 + 2х3 + 6х4 ≤ 8
5x1 + 8х2 + 4х3 + 3х4 ≤ 48
xj ≥ 0, j = 1, 2, 3, 4.
В этой модели функциональные ограничения отражают условия ограниченности объемов используемых в производстве ресурсов.
Проверим, как удовлетворяется система функциональных ограничений оптимальным планом X* = (x1 = 0, x2 = 3, х3 = 1, х4 = 0):
2*0 + 4*3 + 8*0 = 12
7*0 + 2*3 + 2*1 + 6*0 = 8
5*0 + 8*3 + 4*1 + 3*0 = 28 < 48.
Значение целевой функции на этом плане равно
f(X) = 3×0 + 4×3 + 3×1 + 1×0 = 15.
Двойственная задача имеет вид:
min (12y1 + 8y2 + 48у3)
2у1 + 7y2 + 5y3 ≥ 3
4y1 + 2y2 + 8y3 ≥ 4
2y2 + 4y3 ≥ 3
8y1 + 6y2 + 3y3 ≥ 1
y1,2,3 ≥ 0.
Для нахождения оценок у1, у2, у3 используем вторую теорему двойственности. Поскольку третье ограничение в (*) выполняется как строгое неравенство, то у3 = 0. Так как х2 > 0 и x3 > 0, то:
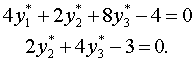
Итак, для получения двойственных оценок имеем систему линейных уравнений:
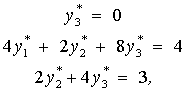
т.е. 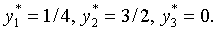
Вычислим значение целевой функции двойственной задачи:
φ(Y) = 12×1/4 + 8×3/2 + 48×0 = 15, т.е. f(X*) = φ(Y*) = 15.
По первой теореме двойственности мы можем утверждать, что действительно найдены оптимальные значения двойственных переменных.
Экономико-математический анализ оптимальных решений базируется на свойствах двойственных оценок. В пределах устойчивости двойственных оценок (для определения этих границ существуют математические соотношения [1], которые реализованы в «Отчете по устойчивости» Excel) имеют место следующие свойства.
1. Величина двойственной оценки того или иного ресурса показывает насколько возросло бы максимальное значение целевой функции, если бы объем данного ресурса увеличился на одну единицу (двойственные оценки измеряют эффективность малых приращений объемов ресурсов в конкретных условиях данной задачи).
В рассматриваемом примере увеличение фонда времени работы станка С1 на 1 час привело бы к росту максимальной суммы прибыли на 0,25 у.е. (у1 = 1/4), а увеличение фонда рабочего времени третьего станка не повлияет на оптимальный план выпуска продукции и сумму прибыли.
Сказанное позволяет выявить направления «расшивки» узких мест, обеспечивающие получение наибольшего экономического эффекта, а также целесообразность изменения в структуре выпуска продукции с позиций общего оптимума.
2. Двойственные оценки отражают сравнительную дефицитность различных видов ресурсов в отношении принятого в задаче показателя эффективности. Оценки показывают, какие ресурсы являются более дефицитными (они будут иметь самые высокие оценки), какие менее дефицитными и какие совсем недефицитны (избыточны).
В примере 3 недефицитным ресурсом является фонд рабочего времени станка С3 поскольку у3 = 0.
Острее ощущается дефицитность ресурса С2 (у2 = 3/2) - он более дефицитен, чем ресурс С2 (у1= 1/4).
3. Двойственные оценки позволяют определять своеобразные «нормы заменяемости ресурсов»: имеется в виду не абсолютная заменяемость ресурсов, а относительная, т.е. заменяемость с точки зрения конечного эффекта и лишь в конкретных условиях данной задачи.
В нашем примере относительная заменяемость ресурсов определяется соотношением (нормой) 1/4 : 3/2 = 1:6.
4. Двойственные оценки служат инструментом определения эффективности отдельных хозяйственных решений (технологических способов), с их помощью можно определять выгодность производства новых изделий, эффективность новых технологических способов:
если 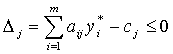 - выгодно,
- выгодно,
если Δj > 0 - невыгодно.
Предположим в рассматриваемом примере следует решить вопрос о целесообразности включения в программу производство деталей нового (пятого) вида при затратах ресурсов станков: 8, 2 и 3 соответственно и ожидаемой удельной прибыли в: а) 6 у.е.; б) 1 у.е.
С учетом сказанного будем иметь в двух рассматриваемых случаях:
в случае а) - 1/4×8 + 3/2×2 + 3×0 - 6 = - 1 < 0 — выгодно расширение ассортимента;
в случае б) - 1/4×8 + 3/2×2 + 3×0 - 1 = 4 > 0 — невыгодно.
Ответим на вопрос, как изменится объем выпуска продукции и прибыль от ее реализации, если фонд рабочего времени станка С1 увеличится на 2 часа, а фонд рабочего времени станка С2 уменьшится на 1 час?
Предполагая, что эти изменения проходят в пределах устойчивости двойственных оценок (уметь проверить!) имеем:
2*0 + 4x2 +8*04 = 14
7*0 + 2x2 + 2x3 + 6*0 = 7.
Отсюда определяется план выпуска в новых производственных условиях -Х= (х1 = 0; х2 = 3,5; х3 = 0; х4 = 0) соответственно прибыль составит 14 у.е., т.е. уменьшится на 1 у.е.
В заключении рассмотрим наш сквозной пример задачи о выборе производственной программы.
| Исходная задача | Двойственная задача |
| max f(X)= 2x1 + 3x2 | min φ(Y) = 300y1 + 150y2 |
| x1 + 3x2 ≤ 300 | y1 + y2 ≥ 2 |
| x1 + x2 ≤ 150 | 3y1 + y2 ≥ 3 |
| x1 ≥ 0, x2 ≥ 0 | y1 ≥ 0, y2 ≥ 0. |
Поскольку в оптимальном плане исходной задачи
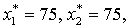 т.е. х1, x2
> 0, то по теореме о дополняющей нежесткости для двойственных оценок имеют
место равенства:
т.е. х1, x2
> 0, то по теореме о дополняющей нежесткости для двойственных оценок имеют
место равенства:
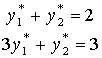
Из этой системы получаем 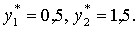
Двойственные оценки найдены правильно, поскольку:
φ(Y*) = 300×0,5 + 150×1,5 = 375 = f(X*).
Таким образом, оба ресурса, участвующие в производстве, дефицитны. При этом с позиции максимизации выручки более дефицитен второй ресурс. Прирост объема первого ресурса на единицу дает приращение выручки на 0,5 у.е., второго ресурса — на 1,5 у.е., т.е. сравнительная норма взаимозаменяемости составляет 1:3 (в пределах устойчивости двойственных оценок).
2.2. Специальные задачи линейного программирования
Специфика ограничений некоторых задач линейного программирования позволяет для их решения использовать специальные алгоритмы, применение которых оказывается менее трудоемким, чем применение симплексного метода. Примером такой задачи является классическая транспортная задача и различные ее модификации.
Для успешного решения транспортной задачи (ТЗ) необходимо знать как [1]:
1) получить первоначальное распределение поставок;
2) оценить оптимальность полученного распределения поставок (например методом потенциалов [1]);
3) перейти к улучшенному распределению поставок с помощью перераспределения поставки по циклу;
4) оценить единственность полученного оптимального плана перевозок.
В [1] рассмотрен пример решения транспортной задачи, в [7] - задача о назначениях.
Методы решения транспортной задачи могут применяться к решению экономических задач, не имеющих ничего общего с транспортировкой груза, поэтому величины cj могут иметь различный смысл в зависимости от конкретной задачи (оптимальное закрепление за станками операций по обработке деталей; оптимальные назначения или проблема выбора; задачи размещения с учетом транспортных и производственных затрат и др.).
Для понимания теории и практики решения этих задач необходимо хорошо усвоить суть и алгоритм решения транспортной задачи [1], решение ТЗ средствами пакета Excel проводится аналогично решению обычной ЗЛП [5].
2.3. Общие сведения о методах реализации моделей нелинейного и динамического программирования
Задача (модель) нелинейного программирования (НЛП) формулируется так же, как и общая задача оптимального программирования со следующими требованиями к целевой функции (ЦФ) и допустимой области: целевая функция f(x1, x2, …, xn) и (или) одна из функций gi(x1, x2, …, xn) являются нелинейными:
min (max)f(x1, x2, ..., хn),
gi(x1, x2, ..., xn){≤, =, ≥}bi, i = 1, 2, ..., m,
xj ≥ 0, j = 1, 2, ..., n.
У произвольной задачи НЛП некоторые или все свойства, характерные для задач ЛП, отсутствуют [1]. Вследствие этого задачи НЛП несравнимо сложнее задач ЛП и для них не существует общего универсального метода их решения (аналогично симплексному методу).
Есть целый ряд методов решения задач НЛП, некоторые из них рассмотрены в [1]. В пакете Excel реализован [8] метод множителей Лагранжа, идея которого заключается в преобразовании задачи условной оптимизации в задачу безусловной оптимизации, решение которой производится методами поиска — градиентными методами (метода первого порядка) или методами Ньютона (методы второго порядка). Наиболее распространенными являются градиентные методы.
Следует, на наш взгляд, согласиться с Б. Курицким [8], что для практического решения задачи оптимизации суть этих методов знать не обязательно.
Однако необходимо помнить, что существующие методы дают возможность находить только локальные оптимумы (помимо случаев, когда задачи обладают соответствующими свойствами выпуклости и вогнутости [1]). Если же есть подозрение, что в допустимой области ЦФ может иметь несколько оптимумов, то эту область следует разбить на ряд областей и в каждой из них определить свои локальные оптимумы, а затем из всех локальных оптимумов выбрать глобальный. В таком практическом подходе задача поиска глобального оптимума сводится к решению ряда задач, в которых ищется свой (локальный) оптимум.
Следует отметить, что в подавляющем большинстве практических задач оптимизации существует только один оптимум [8].
Решение задачи НЛП (реализация модели нелинейной оптимизации) средствами Excel отличается от решения ЗЛП следующим:
назначаются начальные значения искомых переменных
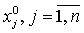 так, чтобы ЦФ в начальной точке не была
равна нулю,
так, чтобы ЦФ в начальной точке не была
равна нулю, 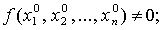
в диалоговом окне Поиска решения в режиме Параметры не надо вводить «Линейная модель».
В Excel признаком достижения оптимума является величина относительного
приращения ЦФ на каждой итерации 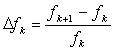 . Оптимум
считается достигнутым, если выполняется условие Δfk
≤ Δfзад, где Δfзад - точность, назначаемая
при решении задачи (Параметры).
. Оптимум
считается достигнутым, если выполняется условие Δfk
≤ Δfзад, где Δfзад - точность, назначаемая
при решении задачи (Параметры).
Примером задачи НЛП является модель оптимального формирования портфеля ценных бумаг (модель Марковица минимального риска).
В этой модели приняты следующие обозначения:
xj,
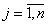 - доля капитала, потраченная на покупку
ценных бумагу j-го вида (весь выделенный капитал принимается за 1);
- доля капитала, потраченная на покупку
ценных бумагу j-го вида (весь выделенный капитал принимается за 1);
mj - средняя ожидаемая доходность
j-й ценной бумаги, 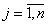 (mj
называют эффективностью j-и ценной бумаги);
(mj
называют эффективностью j-и ценной бумаги);
vj - дисперсия случайной доходности
j-й ценной бумаги, 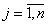 (
(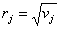 называют риском j-й ценной бумаги).
называют риском j-й ценной бумаги).
В предположении о некоррелированности ценных бумаг (их независимости) модель Марковица имеет вид:
Найти xj,
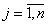 , минимизирующие риск портфеля ценных
бумаг
, минимизирующие риск портфеля ценных
бумаг
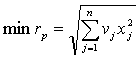 (1)
(1)
при условии, что обеспечивается заданное значение эффективности портфеля mp, т.е.
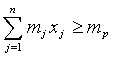 (2)
(2)
и условии, что весь выделенный для инвестиций капитал в целях моделирования принимается за 1, т.е.
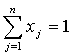 (3)
(3)
xj ≥ 0,
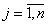 . (4)
. (4)
В модели (1)—(4) нелинейной является ЦФ.
Задачи оптимизации, в результате решения которых искомые значения переменных должны быть целыми числами, называются задачами (моделями) целочисленного (дискретного) программирования:
min(max) f (x1, x2,...,xn);
gi (x1, х2,...,
хn){≤, =, ≥}bi,
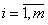 ;
;
xj - целые неотрицательные ∀j∈< n' >.
Если множество индексов <n'>=<n>= {1, 2, ..., n}, то задачу называют полностью целочисленной, если <n'>⊂<n> , то - частично целочисленной.
Существуют различные методы решения задач дискретного программирования (дискретной оптимизации). Наиболее часто используемым методом является метод ветвей и границ. Именно этот метод реализован в программе Поиск решения пакета Excel.
Дискретная оптимизация средствами Excel проводится аналогично решению соответствующих непрерывных задач. Основное отличие заключается во вводе при оформлении диалогового окна Поиск решения требования целочисленности соответствующих переменных (при этом в режиме Параметры устанавливается тип задачи - линейная или нелинейная).
Исходя из требования целочисленности в случае дискретной оптимизации возможен вызов только одного Отчета по результатам.
Достаточно часто при моделировании экономических процессов используется особый случай дискретности задачи - булевость переменных, т.е. переменные могут принимать значения 0 или 1 . Характерным примером этого случая является задача о назначениях.
Постановка задачи. Имеется n видов работ и m исполнителей этих работ. Известны экономические оценки эффекта Cij, i = 1, 2, …, n, j = 1, 2, …, m; от назначения i-го исполнителя j-й вид работ. Требуется так распределить исполнителей по видам работ, чтобы суммарный эффект от назначений был максимальным.
ЭММ. Введем необходимые обозначения, пусть
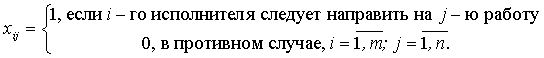
Тогда математически задачу о назначениях можно записать в виде:
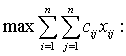
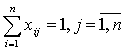 (на каждую работу должен
быть назначен исполнитель);
(на каждую работу должен
быть назначен исполнитель);
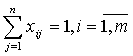 (все исполнители должны
получить назначение).
(все исполнители должны
получить назначение).
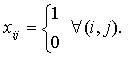 (*)
(*)
Для реализации этой ЭММ средствами Excel ограничение (*) в рабочей таблице Excel следует записать в виде:
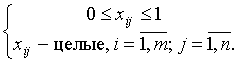
(Этот прием используется во всех дискретных задачах с булевыми переменными.)
Отметим некоторые особые случаи приведенной задачи.
1. Если по той или иной причине некоторое назначение является недопустимым, то соответствующий элемент матрицы (Cij)m×n принимается равным (-М), т.е. его значение заведомо меньше любого другого значения. После этого в ходе решения мы сможем избежать данного назначения автоматически.
2. Если матрица (Cij)m×n
не является квадратной, то по аналогии с открытой транспортной задачей в
модели задачи о назначениях следует записать либо ограничение
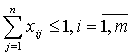 (число исполнителей m больше числа
работ n) или
(число исполнителей m больше числа
работ n) или 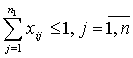 (число исполнителей
m меньше числа работ n).
(число исполнителей
m меньше числа работ n).