Тема 1. Оптимизационные экономико-математические модели
Тема 2. Методы получения оптимальных решений
Тема 4. Методы и модели анализа экономических процессов
Тема 5. Прогнозирование экономических процессов с использованием временных рядов
Тема 6. Производственные функции
Тема 7. Методы и модели управления и принятия решений в экономических системах
Тема 5. Прогнозирование экономических процессов с использованием временных рядов
5.1. Методология экономического прогнозирования. Основные этапы построения моделей экономического прогнозирования. Классификация методов экономического прогнозирования.
5.2. Характеристика типов кривых роста. Методы выбора наилучшей кривой роста. Методы вычисления параметров кривых роста: Критерии адекватности и точности моделей экономического прогнозирования. Экстраполяция экономических процессов с использованием кривых роста. Точечные и интервальные прогнозы.
5.3. Адаптивные методы прогнозирования. Адаптивная модель Брауна: алгоритм разработки, оценка качества и использование для целей прогнозирования.
5.1. Экономическое прогнозирование (ЭП)
ЭП - это процесс разработки экономических прогнозов, основанных на научных методах познания экономических явлений и использования всей совокупности методов, средств и способов экономической прогностики. В то же время ЭП является частью прогностики - прикладной научной дисциплины, изучающей закономерности и способы разработки прогнозов развития объектов любой природы. ЭП в качестве объекта рассматривает процесс конкретного расширения воспроизводства, а в качестве предмета - познание возможных состояний функционирующих экономических объектов в будущем, исследование закономерной и способов разработки экономических прогнозов.
После того, как предварительный анализ информации убедил нас в том, что данные сопоставимы, однородны, аномальных наблюдений нет, число наблюдений достаточно для проявления тенденций, исследуемый процесс устойчив, а тенденция прослеживается отчетливо, можно приступать к подбору трендовых моделей и разработке прогноза.
Идея социально-экономического прогнозирования базируется на предположении, что закономерность развития, действовавшая в прошлом (внутри ряда экономической динамики), сохранится и в прогнозируемом будущем. В этом смысле прогноз основан на экстраполяции. Экстраполяция, проводимая в будущее, называется перспективной, а в прошлое — ретроспективной. Обычно, говоря об экстраполяции рядов динамики, подразумевают перспективную экстраполяцию.
Теоретический основой распространения тенденции на будущее является такое свойство социально-экономических явлений, как инерционность. Именно инерционность позволяет выявить сложившиеся взаимосвязи как между уровнями динамического ряда, так и между группой связных рядов динамики. Прогнозирование методом экстраполяции базируется на следующих предпосылках: а) развитие исследуемого явления в целом следует описывать плавной кривой; б) общая тенденция развития явления в прошлом и настоящем не должна претерпевать серьезных изменений в будущем; в) учет случайности позволяет оценить вероятность отклонения от закономерного развития. Поэтому надежность и точность прогноза зависят от того, насколько близкими к действительности окажутся эти предположения, а так же, как точно удалось охарактеризовать выявленную в прошлом закономерность.
5.2. Характеристика типов кривых роста
Плавную кривую (гладкую функцию), аппроксимирующую временной ряд, принято называть кривой роста. Собственно подбор такой кривой является аналитическим (немеханическим) выравниванием. Чаще всего используются полиноминальные, экспоненциальные и S-образные кривые роста.
Экстраполяцию кривой роста
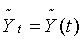 на будущее в общем виде можно представить
формулой
на будущее в общем виде можно представить
формулой
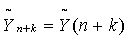 (5.2.1)
(5.2.1)
где 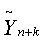 — прогнозируемый уровень;
n — номер последнего фактического уровня ряда динамики; k
— период упреждения.
— прогнозируемый уровень;
n — номер последнего фактического уровня ряда динамики; k
— период упреждения.
Замечание. Чем шире раздвигаются временные рамки прогнозирования, тем очевиднее становится недостаточность простого экстраполяционного метода (могут меняться тенденции, неизвестны точки поворота кривых, влияние новых факторов и т.д.). В этом случае динамичность экономических явлений и процессов вступает в противоречие с инерционностью их развития. Так как анализируемые ряды экономической динамики нередко относительно короткие, то временной горизонт экстраполяции не может быть бесконечным. Поэтому, чем короче срок экстраполяции (период упреждения), тем более надежные и точные результаты (при прочих равных условиях) дает прогноз. За короткий период не успевают сильно измениться условия развития явления и характер его динамики.
Экстраполяция дает возможность получить точечное значение прогноза. Точное совпадение фактических данных и прогностических точечных оценок, полученных путем экстраполяции кривых, характеризующих тенденцию, имеет малую вероятность. Возникновение соответствующих отклонений объясняется следующими причинами. Во-первых, выбранная для прогнозирования кривая не является единственно возможной для описания тенденции; можно подобрать такую кривую, которая дает более точные результаты. Во-вторых, прогноз осуществляется на основании ограниченного числа исходных данных; кроме того, каждый исходный уровень обладает еще случайной компонентой, поэтому и кривая, по которой осуществляется экстраполяция, будет содержать случайную компоненту. В-третьих, тенденция характеризует лишь движение среднего уровня ряда динамики, поэтому отдельные наблюдения от него отклоняются. Если такие отклонения наблюдались в прошлом, то они будут наблюдаться и в будущем.
Экстраполяционное прогнозирование экономических процессов, представленных одномерными временными рядами наблюдений, сводится к выполнению следующих основных этапов: 1) предварительный анализ данных; 2) формирование набора аппроксимирующих функций (кривых роста); 3) численное оценивание параметров моделей-кандидатов; 4) проверка адекватности моделей; 5) оценка точности адекватных моделей; 6) выбор лучшей модели; 7) расчет точечного и интервального прогнозов.
Вычисление параметров кривых роста методом наименьших квадратов. Формирование набора моделей, одна из которых будет использована для получения прогноза, происходит на основе интуитивных приемов (таких, например, как анализ графика динамики ряда), формализованных статистических процедур (исследование приростов уровней), а также содержательного анализа процесса. Предпочтение, как правило, отдается простым моделям, допускающим содержательную интерпретацию. К числу наиболее простых относятся линейные модели роста
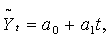 (5.2.2)
(5.2.2)
где а0 и a1 - параметры модели, а t =1, 2, ..., n.
Рассмотрим оценку параметров модели по методу, сводящемуся к поиску таким значений a0 и а1, при которых сумма квадратов отклонений эмпирических данных от расчетной прямой (5.2.2) является наименьшей (метод наименьших квадратов (МНК). Математически критерий такой оценки параметров записывается в виде:
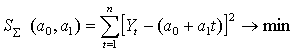 (5.2.3)
(5.2.3)
Для нахождения минимума функции двух переменных S∑(a0, a1) следует взять частные производные по a0 и a1, a затем приравнять их нулю. В результате получим так называемую систему нормальных уравнений:
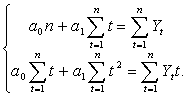 (5.2.4)
(5.2.4)
Решая эту систему двух линейных уравнений с двумя неизвестными, получим
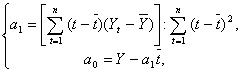 (5.2.5)
(5.2.5)
где 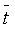 , и
, и
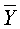 — среднее значения, соответственно, моментов
наблюдения и уровней ряда.
— среднее значения, соответственно, моментов
наблюдения и уровней ряда.
Критерии адекватности моделей экономического прогнозирования.
Важным этапом прогнозирования социально-экономических процессов является
проверка адекватности модели реальному явлению. Для ее осуществления исследуют
ряд остатков 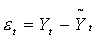 , т.е. отклонений расчетных
значений от фактических. Если трендовая модель выбрана правильно, то для
остатков характерны: равенство нулю математического ожидания, случайный
характер отклонений от математического ожидания, отсутствие автокорреляции
и неизменность дисперсии остатков во времени, нормальный закон распределения.
Рассмотрим перечисленные требования подробнее.
, т.е. отклонений расчетных
значений от фактических. Если трендовая модель выбрана правильно, то для
остатков характерны: равенство нулю математического ожидания, случайный
характер отклонений от математического ожидания, отсутствие автокорреляции
и неизменность дисперсии остатков во времени, нормальный закон распределения.
Рассмотрим перечисленные требования подробнее.
1. Проверка равенства математического ожидания уровней ряда остатков нулю осуществляется в ходе проверки соответствующей нулевой гипотезы H0:|ε|=0. С этой целью строится t-статистика
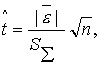 (5.2.6)
(5.2.6)
где 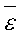 - среднее арифметическое
значение уровней ряда остатков εt;
- среднее арифметическое
значение уровней ряда остатков εt;
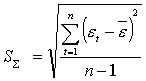 - среднеквадратическое отклонение
для этой последовательности, рассчитанное по формуле для малой выборки.
- среднеквадратическое отклонение
для этой последовательности, рассчитанное по формуле для малой выборки.
На уровне значимости λ гипотеза отклоняется, если
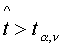 , где tα,ν
- критерий распределения Стьюдента с доверительной вероятностью (1 -
α) и v = n - 1 степенями свободы.
, где tα,ν
- критерий распределения Стьюдента с доверительной вероятностью (1 -
α) и v = n - 1 степенями свободы.
2. Для проверки условия случайности возникновении отдельных отклонений от тренда часто используется критерий, основанный на поворотных точках. Значение случайной переменной считается поворотной точкой, если оно одновременно больше соседних с ним элементов или, наоборот, меньше значений предыдущего и последующего за ним члена. Если остатки случайны, то поворотная точка приходится примерно на каждые 1,5 наблюдения. Если их больше, то возмущения быстро колеблются, и это не может быть объяснено только случайностью. Если же их меньше, то последовательные значения случайного компонента положительно коррелированны.
Существует определенная зависимость между средней арифметической
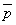 , дисперсией
, дисперсией 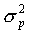 ;
количества поворотных точек р и числом членов исходного ряда наблюдений
n. В случайной выборке средняя арифметическая (математическое ожидание)
числа поворотных точек равна
;
количества поворотных точек р и числом членов исходного ряда наблюдений
n. В случайной выборке средняя арифметическая (математическое ожидание)
числа поворотных точек равна 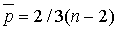 , а их дисперсия
вычисляется по формуле
, а их дисперсия
вычисляется по формуле 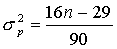 . Учитывая эти
соотношения, критерий случайности отклонений от тренда при уровне вероятности
0,95 можно представить, как
. Учитывая эти
соотношения, критерий случайности отклонений от тренда при уровне вероятности
0,95 можно представить, как
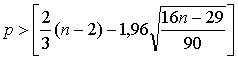 (5.2.7)
(5.2.7)
где р — фактическое количество поворотных точек в случайном ряду;
1,96 — квантиль нормального распределения для 5%-го уровня значимости;
квадратные скобки означают, что от результата вычисления следует взять целую часть (не путать с процедурой округления!).
Если неравенство не соблюдается, то ряд остатков нельзя считать случайным (т.е. он содержит регулярную компоненту), и стало быть, модель не является адекватной.
3. Наличие (отсутствие) автокорреляции в отклонениях от модели роста проще всего проверить с помощью критерия Дарбина—Уотсона. С этой целью строится статистика Дарбина— Уотсона (d-статистика), в основе которой лежит расчетная формула
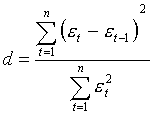 (5.2.8)
(5.2.8)
Теоретическое основание применения этого критерия обусловлено тем, что в динамических рядах как сами наблюдения, так и отклонения от них распределяются в хронологическом порядке.
При отсутствии автокорреляции значение d примерно равно 2, а при полной автокорреляции - 0 или 4. Следовательно, оценки, получаемые по критерию, являются не точечными, а интервальными. Верхние (d2) и нижние (d1) критические значения, позволяющие принять или отвергнуть гипотезу об отсутствии автокорреляции, зависят от количества уровней динамического ряда и числа независимых переменных модели. Значения этих границ для трех уровней значимости (а = 0,01, а = 0,025 и а = 0,05) даны в специальных таблицах (см. табл. II). При сравнении расчетного значения d-статистики (5.2.8) с табличным могут возникнуть такие ситуации: d2 < d < 1 — ряд остатков не коррелирован; d < d1 — остатки содержат автокорреляцию; d1 < d < d2 — область неопределенности, когда нет оснований ни принять, ни отвергнуть гипотезу о существовании автокорреляции. Если d превышает 2, то это свидетельствует о наличии отрицательной корреляции. Перед входом в таблицу такие значения следует преобразовать по формуле d' = 4 - d.
Установив наличие автокорреляции остатков, надо улучшать модель. Если же ситуация оказалась неопределенной, применяют другие критерии. В частности, можно воспользоваться первым коэффициентом автокорреляции:
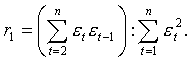 (5.2.9)
(5.2.9)
Для суждения о наличии или отсутствии автокорреляции в исследуемом ряду фактическое значение коэффициента автокорреляции (5.2.9) сопоставляется с табличным (критическим) для 5%-го или 1%-го уровня значимости (вероятности допустить ошибку при принятии нулевой гипотезы о независимости уровней рада) (см. табл. III). Если фактическое значение коэффициента автокорреляции меньше табличного, то гипотеза об отсутствии автокорреляции в ряду может быть принята. Когда же фактическое значение больше табличного, делают вывод о наличии автокорреляции в ряду динамики.
4. Соответствие рада остатков нормальному закону распределения проверим с помощью R/S-критерия:
R/S = (εmax - εmin ):Sv, (5.2.10)
где εmax и εmin - максимальный и минимальный уровни рада остатков соответственно;
Sv — среднеквадратическое отклонение.
Если расчетное значение (5.2.10) попадает между табулированными границами (см. табл. IV) с заданным уровнем вероятности, то гипотеза о нормальном распределении рада остатков принимается. В этом случае допустимо строить доверительный интервал прогноза.
Если все четыре пункта проверки 1-4 дают положительный результат, делается вывод о то, что выбранная трендовая модель является адекватной реальному раду экономической динамики. Только в этом случае ее можно использовать для построения прогнозных оценок. В противном случае модель надо улучшать.
Оценка точности модели имеет смысл только для адекватных моделей. В случае временных радов точность модели определяется как разность меду фактическим и расчетным значениями. В качестве статистических показателей точности чаще всего применяют стандартную ошибку прогнозируемого показателя, или среднеквадратическое отклонение от линии тренда —
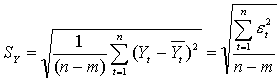 (5.2.11)
(5.2.11)
где m — число параметров модели, и среднюю относительную ошибку аппроксимации -
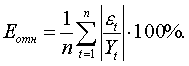 (5.2.12)
(5.2.12)
Если ошибка, вычисленная по формуле (5.2.12), не превосходит 15%, точность модели считается приемлемой. В общем случае допустимый уровень точности, а значит и надежности устанавливает пользователь модели, который в результате содержательного анализа проблемы выясняет, насколько она чувствительна к точности решения и насколько велики потери из-за неточного решения.
Построение точечного и интервального прогнозов. Если в ходе проверки разрабатываемая модель признана достаточно надежной, на ее основе разрабатывается точечный прогноз (5.2.1). Он получается путем подстановки в модель значений времени t, соответствующих периоду упреждения k: t = n + k. Так, в случае трендовой модели в виде полинома первой степени - линейной модели роста (5.2.2) - экстраполяция на k шагов вперед имеет вид:
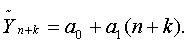 (5.2.13)
(5.2.13)
Для учета случайных колебаний при прогнозировании рассчитываются доверительные интервалы, зависящие от стандартной ошибки (5.2.11), горизонта прогнозирования k, длины временного ряда n и уровня значимости прогноза а. В частности, для прогноза (5.2.13) будущие значения Yn+k c вероятностью (1 - а) попадут в интервал
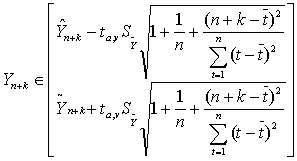 (5.2.14)
(5.2.14)
Построение прогноза по полиному первой степени. В качестве примера рассмотрим разработку трендовой модели и получение прогнозных оценок динамики ВВП России на основе реального временного ряда, представленного в табл. 5.2.1
Таблица 5.2.1
Динамика ВВП России
| Дата | ВВП (млрд руб.) | |
|---|---|---|
| 1 | 1,99 | 238 |
| 2 | 2,99 | 249 |
| 3 | 3,99 | 287 |
| 4 | 4,99 | 340 |
| 5 | 5,99 | 342 |
| 6 | 6,99 | 373 |
| 7 | 7,99 | 360 |
| 8 | 8,99 | 380 |
| 9 | 9,99 | 403 |
| 10 | 10,99 | 419,08 |
| 11 | 11,99 | 451 |
| 12 | 12,99 | 460 |
| 13 | 1,00 | 379,8 |
| 14 | 2,00 | 410,7 |
Источник: Коммерсант. 2000. 3 мая. № 77.
Для того чтобы оценить параметры и качество этой модели (адекватность и точность), а также построить точечный и интервальный прогнозы, можно воспользоваться ППП СтатЭксперт, Пакетом анализа в EXCEL [4] или выполнить соответствующие расчеты вручную, используя калькулятор.
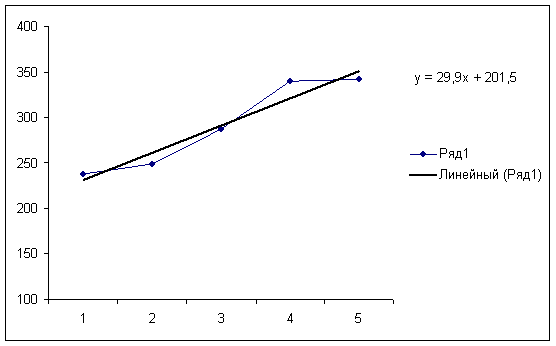
По данным табл. 5.2.1 средствами EXCEL построим график динамики ВВП, на котором обозначим предполагаемый тренд (рис. 5.2) и прогноз на месяц вперед.
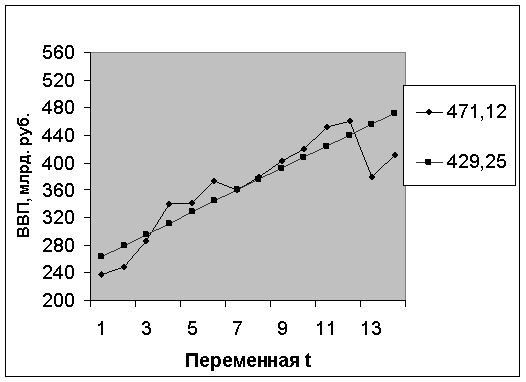
Рис. 5.2. Динамика ВВП России (млрд. руб.)
Перебирая варианты аппроксимирующих кривых, мы остановились на линейной функции, как наиболее подходящей. Графическая экстраполяция функции на шаг вперед дает на март 2000 года предполагаемое значение ВВП около 475 млрд. руб.
Для того чтобы оценить параметры и качество этой модели (адекватность и точность), а также построить точечный и интервальный прогнозы, заполним рабочую таблицу 5.2.2.
В первой нижней строке под таблицей (в «подвале») записаны суммы соответствующих граф, во второй - соответствующие средние значения (если они фигурируют в дальнейших расчетах). Следуя формулам (5.2.5), по суммам граф 4 и 6 оценим параметры линейной модели роста: а0 = 256,36 и а1 = 14,32. Таким образом, искомая модель принимает вид:
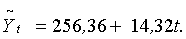
Последовательно подставляя в (5.2.2) вместо фактора t его значения от 1 до n = 14, заполним графу расчетных уровней 7. Вычитая далее из элементов графы 2 соответствующие элементы графы 7, заполним графу ряда остатков 8.
Таблица 5.2.2
| t | Yt | 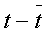 |
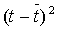 |
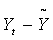 |
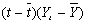 |
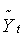 |
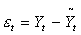 |
Точ. пов. | 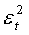 |
εt - εt-1 | (εt - εt-1)2 | εtεt-1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 1 | 238,00 | -6,5 | 42,25 | -125,76 | 817,44 | 270,68 | -32,68 | - | 1067,98 | - | - | - |
| 2 | 249,00 | -5,5 | 30,25 | -114,76 | 631,18 | 285,00 | -36,00 | 1 | 1296,00 | -3,32 | 11,02 | 1176,48 |
| 3 | 287,00 | -4,5 | 20,25 | -76,76 | 345,42 | 299,32 | -12,32 | 0 | 151,78 | 23,68 | 560,74 | 443,52 |
| 4 | 340,00 | -3,5 | 12,25 | -23,76 | 83,16 | 313,64 | 26,36 | 1 | 694,85 | 38,68 | 1496,14 | -324,76 |
| 5 | 342,00 | -2,5 | 6,25 | -21,76 | 54,4 | 327,96 | 14,04 | 1 | 197,12 | -12,32 | 151,78 | 370,09 |
| 6 | 373,00 | -1,5 | 2,25 | 9,24 | -13,86 | 342,28 | 30,72 | 1 | 943,72 | 16,68 | 278,22 | 431,31 |
| 7 | 360,00 | -0,5 | 0,25 | -3,76 | 1,88 | 356,60 | 3,40 | 1 | 11,56 | -27,32 | 746,38 | 104,45 |
| 8 | 380,00 | 0,5 | 0,25 | 16,24 | 8,12 | 370,92 | 9,08 | 0 | 82,45 | 5,68 | 32,26 | 30,87 |
| 9 | 403,00 | 1,5 | 2,25 | 39,24 | 58,86 | 385,24 | 17,76 | 0 | 315,42 | 8,68 | 75,34 | 161,26 |
| 10 | 419,10 | 2,5 | 6,25 | 55,34 | 138,35 | 399,56 | 19,54 | 0 | 381,81 | 1,78 | 3,16 | 347,03 |
| 11 | 451,00 | 3,5 | 12,25 | 87,24 | 305,34 | 413,88 | 37,12 | 1 | 1377,89 | 17,58 | 309,05 | 725,32 |
| 12 | 460,00 | 4,5 | 20,25 | 96,24 | 433,08 | 428,20 | 31,80 | 0 | 1011,24 | -5,32 | 28,30 | 1180,42 |
| 13 | 379,80 | 5,5 | 30,25 | 16,04 | 88,22 | 442,52 | -62,72 | 1 | 3933,80 | -94,52 | 8934,03 | -1994,5 |
| 14 | 410,70 | 6,5 | 42,25 | 46,94 | 305,11 | 456,84 | -46,14 | - | 2128,90 | 16,58 | 274,89 | 2893,90 |
| 105 | 5092,6 | 0 | 227,50 | -0,04 | 3256,70 | 5092,64 | -0,04 | 7 | 13594,52 | 12901,31 | 5545,40 | |
| 7.5 | 363,76 |
Замечание. Суммы 7 и 8 граф вместе должны давать сумму графы 2.
Для проверки адекватности модели в соответствии с видом формул (5.2.6), (5.2.8) и (5.2.9) организуем и заполним графы 9-13.
1. Легко убедиться, что математическое ожидание ряда остатков
равно нулю, т.е. 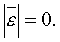
2. Проверка случайности ряда остатков по критерию пиков дает положительный результат: 7 (сумма графы 9) больше 5 (критическое число поворотных точек, рассчитанное по формуле (5.2.6)).
3. При проверке независимости уровней ряда остатков друг от друга значение d = 0,95, вычисленное по формуле (5.2.8), при уровне значимости а = 0,025 попадает в интервал между d1 = 0,920 и d2 = 1,060, т.е. в область неопределенности. Поэтому придется воспользоваться формулой (5.2.9): r1 = 0,41. Сопоставляя это число с табличным значением первого коэффициента автокорреляции 0,485, взятым для уровня значимости а = 0,01 и n = 14, увидим, что расчетное значение меньше табличного. Это означает, что с ошибкой в 1% ряд остатков можно считать некоррелированным, т.е. свойство взаимной независимости уровней остаточной компоненты подтверждается.
4. Соответствие ряда остатков нормальному распределению установим с помощью формулы (5.2.10). Вычислим вариационный размах (99,84) и среднеквадратическое отклонение SE = 32,34. По этим данным рассчитаем критерий R/S — 3,09. Для n = 14 и а = 0,05 найдем критическим интервал: [2,92; 4,05]. Вычисленное значение 3,09 попадает между табулированными границами с заданным уровнем вероятности. Значит, закон нормального распределения выполняется, и можно строить доверительный интервал прогноза.
5. Так как модель оказалась адекватной, оценим ее точность. По формуле (5.2.12) рассчитаем среднюю относительную ошибку: Еотн = 7,7%. Такую ошибку можно считать приемлемой.
6. Экстраполяция уравнения
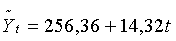 на шаг вперед, т.е. на момент времени
n + 1 = 15, дает прогнозное значение ВВП на март 2000 года, равное
на шаг вперед, т.е. на момент времени
n + 1 = 15, дает прогнозное значение ВВП на март 2000 года, равное
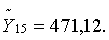
7. Для построения интервального прогноза рассчитаем доверительный интервал (5.2.14). Примем значение уровня значимости а = 0,3, а значит, доверительную вероятность — 70 %. В этом случае критерий Стьюдента (при v = n - 2 = 12) равен tα,v = 1,083. Вычислив среднеквадратическую ошибку тренда (5.2.11), с учетом значения tα,v получим интервальный прогноз:
Y15∈[471,12-41,87; 471,12+41,87]
Y15∈[429,32; 512,99] (**)
где 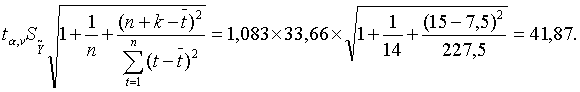
Таким образом, построенная нами модель является полностью адекватной динамике ВВП и достаточно надежной для краткосрочных прогнозов. Поэтому с вероятностью 70% можно утверждать, что при сохранении сложившихся закономерностей развития значение ВВП, прогнозируемое на март 2000 года с помощью линейной модели роста, попадет в промежуток, образованный нижней и верхней границей доверительного интервала (**).
5.3. Адаптивные методы прогнозирования. Адаптивная модель Брауна
Адаптивными методами прогнозирования принято называть такие методы, процесс реализации которых заключается в вычислении последовательных во времени значений прогнозируемого показателя с учетом степени влияния предшествующих уровней. При краткосрочном прогнозировании наиболее важным является не тенденция развития исследуемого процесса, сложившаяся в среднем на всем периоде предыстории, а последние значения этого процесса. Свойство динамичности развития экономического явления здесь преобладает над свойством его инерционности. Поэтому при краткосрочном прогнозировании, как правило, более эффективными оказываются адаптивные методы, учитывающие неравноценность уровней временного ряда и быстро приспосабливающие свою структуру и параметры к изменяющимся условиям.
Рассмотрим один из таких методов - метод Брауна.
Расчетное значение в момент времени получается по формуле
Yp(t) = a0(t - 1) + a1(t - 1)k (5.3.1)
где k - количество шагов прогнозирования (обычно k = 1).
Это значение сравнивается с фактическим уровнем, и полученная ошибка прогноза E(t) = Y(f) – Yp(t) используется для корректировки модели. Корректировка параметров осуществляется по формулам:
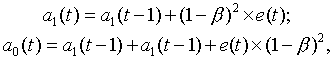 (5.3.2)
(5.3.2)
где β - коэффициент дисконтирования данных, отражающий большую степень доверия к более поздним данным. Его значение должно быть в интервале от 0 до 1.
Процесс модификации модели (t = 1, 2, ..., N) в зависимости от текущих прогнозных качеств обеспечивает ее адаптацию к новым закономерностям развития. Для прогнозирования используется модель, полученная на последнем шаге (при t = N).
Построение прогноза по модели Брауна. Воспользуемся этой схемой адаптивного прогнозирования для примера, рассмотренного выше. Начальные оценки параметров получим по первым пяти точкам при помощи метода наименьших квадратов.
a0(0) = 201,5, a1(0) = 29,9.
Возьмем α = 0,8, k = 1 и β = 1-α = 0,2.
a1(t) = a1(t - 1) + (1 - β)2 × e(t)
a0(t) = a1(t - 1) + a1(t - 1) + e(t) × (1 - β2),
| Время | Факт | a0 | a1 | Расчет | Отклонение |
|---|---|---|---|---|---|
| 201,50 | 29,90 | ||||
| 1 | 238 | 237,74 | 34,12 | 231,40 | 6,600 |
| 2 | 249 | 249,91 | 19,49 | 271,86 | -22,860 |
| 3 | 287 | 286,30 | 30,75 | 269,41 | 17,592 |
| 4 | 340 | 339,08 | 45,44 | 317,05 | 22,951 |
| 5 | 342 | 343,70 | 18,23 | 384,52 | -42,523 |
| 6 | 373 | 372,56 | 25,31 | 361,93 | 11,073 |
| 7 | 360 | 361,51 | 1,08 | 397,87 | -37,870 |
| 8 | 380 | 379,30 | 12,22 | 362,59 | 17,409 |
| 9 | 403 | 402,54 | 19,56 | 391,52 | 11,478 |
| 10 | 419,1 | 419,22 | 17,64 | 422,10 | -3,005 |
| 11 | 451 | 450,43 | 26,69 | 436,86 | 14,139 |
| 12 | 460 | 460,68 | 15,73 | 477,12 | -17,124 |
| 13 | 379,8 | 383,66 | -46,10 | 476,42 | -96,615 |
| 14 | 410,7 | 407,77 | 0,71 | 337,56 | 73,139 |
| 15 | 408,48 |
Прогнозные оценки по модели (5.3.1) получаются путем подстановки в нее значения k = 1, а интервальные - по тем же формулам, что и для кривых роста:
Yp(15) = 407,11 + 0,71×1 = 408,48.
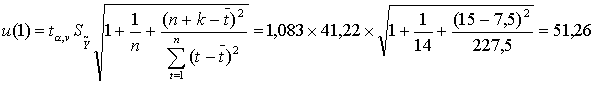
k = 1 (t = 15).
Нижняя граница: 408,48 - 51,26 = 357, 21.
Верхняя граница: 408,48 + 51,26 = 459,75.
Прогнозные оценки по модели Брауна
| Время t | Шаг k | Прогноз Yp(t) | Нижняя граница | Верхняя граница |
|---|---|---|---|---|
| 15 | 1 | 408,48 | 357,21 | 459,75 |
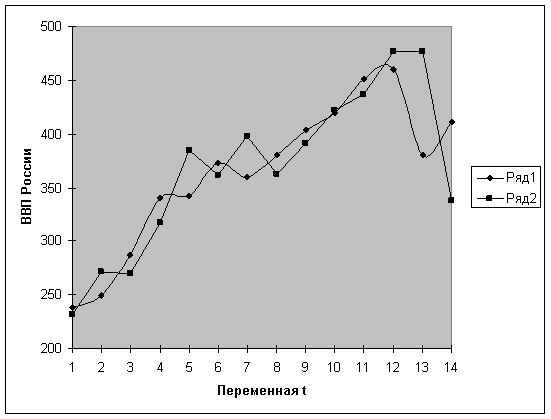
При сохранении сложившихся закономерностей динамики развития прогнозируемая величина с вероятностью 70% (t0,3;12 = 1,0832) попадает в интервал, образованный нижней и верхней границами. На рис. 5.3 представлены результаты аппроксимации и прогнозирования по этой модели.