Глава 1. Образовательная система России
Глава 2. Автоматизация учебного процесса
Глава 3. Основы теории тестирования
Глава 4. Базы заданий для проектирования тестов
Глава 5. Модели и алгоритмы проектирования тестов
Глава 6. Автоматизация проектирования тест-билетов
Глава 7. Методические и технологические аспекты тестирования
Глава 3. Основы теории тестирования.
3.1. Основные понятия теории тестирования.
Появление методов измерения учебных достижений обучаемых связано с работами американских исследователей в конце 19 века, хотя предыстория их уходит в глубокую древность [60]. В начале 20 века были заложены основы теории тестирования, которые активно развивались до начала 70-х годов. Этот период развития теории принято называть классическим, а разработанную теорию - классической теорией тестирования. В 1968 году Ф. Лорд и М. Новик [76-78] сформулировали основные постулаты математической модели классической теории тестирования.
Под тестом Т в классической теории тестирования понимается структурированная система заданий и соответствующая ей процедура проверки этих заданий, обеспечивающая однозначность интерпретации полученных результатов тестирования.
В связи с возрастающим использованием современной компьютерной техники при определении уровня обученности обучаемых и ее широким внедрением в практику работы образовательных организаций возникает задача переосмысления методов и средств классической теории тестирования, формализации процедур и методов, создания технологии тестирования, рассчитанной на массового пользователя.
При этом важным аспектом использования основных понятий классической теории тестирования с целью измерения уровня обученности испытуемых является визуализация результатов измерения в виде форм японского промышленного стандарта JIS: гистограмма, наложение (стратификация) гистограмм, диаграмма Парето, контрольная карта Шухарта и др. [36].
Пусть тест-билет T, составленный из L заданий, был представлен для тестирования группы из N испытуемых. Результаты тестового испытания удобно представить в виде таблицы:
| Тестируемые (испытуемые) | Задания |
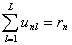 |
|||
|---|---|---|---|---|---|
| 1 | 2 | l | L | ||
| 1 | : | ||||
| 2 | : | ||||
| : | |||||
| n | .. .. | .. .. | unl | ||
| N | |||||
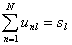 |
|||||
где unl - оценка выполнения l-го задания n-м испытуемым.
Для дихотомических заданий, то есть заданий, оцениваемых в бинарной шкале (верно/неверно):

Для политомических заданий, то есть заданий, оцениваемых в многобалльной шкале ([0,m]): 0 ≤ unl ≤ m.
Матрицу 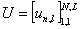 размером N×L
будем называть матрицей ответов, сумму
размером N×L
будем называть матрицей ответов, сумму 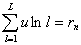 - первичным результатом
тестирования n-го испытуемого, -
- первичным результатом
тестирования n-го испытуемого, - 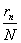 коэффициентом, а
коэффициентом, а 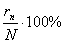 - процентом выполнения тест-билета.
- процентом выполнения тест-билета.
Для анализа и принятия решений по итогам педагогических измерений результаты удобно представить в наиболее наглядной форме. Простыми и удобными формами являются рейтинг-лист и гистограмма.
Под рейтинг-листом будем понимать список испытуемых, упорядоченный в порядке убывания полученных ими баллов (результатов тестирования). Такой упорядоченный список можно представить как для отдельных классов, так и для параллелей классов.
На рейтинг-листе можно отметить границу-минимум процента выполнения данного тест-билета. Это позволяет сразу определить как число испытуемых, не выполнивших тест-билет, так и их фамилии и классы. Четко представлены лидеры тестирования и виден максимальный процент выполнения теста.
Если педагогическое измерение проводится на большом массиве испытуемых, то рейтинг-лист становится очень длинным, поэтому удобно для наглядного представления результатов в целом использовать другую форму представления - гистограмму.
По оси абсцисс откладывается процент выполнения тест-билета, а высота столбцов соответствует доле испытуемых, имеющих результат в заданном процентном интервале. Практика показывает, что в качестве шага удобно выбирать интервал в 5 или 10%.
Таким образом, гистограмма иллюстрирует плотность распределения результатов педагогических измерений и позволяет показать соотношение размеров различных групп испытуемых, получивших низкие, средние или высокие баллы.
Результаты педагогических измерений представляют интерес не только с точки зрения анализа обученности испытуемых, но и с точки зрения качества разработки тест билетов.
Часто перед тем, как перейти к анализу данных по результатам тестирования, проводят выбраковку - удаляют строки и столбцы, состоящие полностью из 0 или 1 (или М для политомических заданий), то есть удаляют задания, которые никто не смог выполнить или, наоборот - абсолютно выполнивших все задания (уровень тест-билета оказался ниже его уровня подготовки).
Отношение
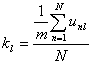
будем называть коэффициентом решаемости l-го задания.
Очевидно, что 0 ≤ ki ≤ 1. Чем больше ki, тем легче данное задание, и, наоборот - чем меньше ki, тем труднее данное задание.
Коэффициент решаемости тест-билета удобно представлять в виде карты Шухарта, где по оси абсцисс откладываются номера заданий в тест-билете, а по оси ординат -коэффициент решаемости.
Коэффициент селективности задания (другие названия - коэффициент чувствительности, дискриминационный индекс, D-индекс) используется как показатель дифференциации обучаемых. В классической теории тестирования разработаны десятки таких показателей (среди многих – бисериальный коэффициент rbis, точечный бисериальный коэффициент rpb, тетрахорический коэффициент rlet, коэффициент χ, ULI (upper-lower-index)). Однако на практике эти показатели примерно одинаково эффективны.
Наиболее простым является коэффициент селективности, определяемый как upper-lower-index:
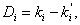
где ki
- коэффициент решаемости i-го
задания лучшей половины тестируемых, 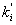 - коэффициент решаемости
i-го задания худшей половины
тестируемых.
- коэффициент решаемости
i-го задания худшей половины
тестируемых.
Очевидно, что -1 ≤ Di ≤ 1. Если задание правильно выполняет больше лучших, чем худших тестируемых, то D>0, в противном случае D<0. Если задание выполнит одинаковое количество лучших и худших, то D=0. Такое задание не дифференцирует тестируемых.
Обычно считается, что для заданий с коэффициентом решаемости 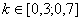 коэффициент
селективности должен быть не менее 0,25. Для заданий с
коэффициент
селективности должен быть не менее 0,25. Для заданий с 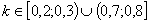 D должен быть не менее 0,15.
D должен быть не менее 0,15.
Т. Kelly [72] показал, что оптимальный уровень селективности достигается, когда популяции тестируемых делятся на лучших и худших не в соотношении 50% : 50%, а в соотношении 27% : 73%.
Точечно-бисериальный коэффициент - часто используемый коэффициент селективности, представляющий собой упрощенную формулу коэффициента корреляции Пирсона между количеством тестируемых, выполнявших данные дихотомические задания, и общим результатом, а именно:
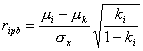
где μi - среднее значение результатов тестирования среди тестируемых, ответивших корректно на i-ое задание, μk -среднее значение результатов тестирования всех тестируемых, σx - среднее квадратичное отклонение результатов тестирования всех тестируемых.ki, - коэффициент решаемости i-го задания.
3.2. Латентное пространство. Характеристические кривые.
Цель любого тестирования (в том числе педагогического) - оценка определенных характеристик личности, которые явно не наблюдаемы и поэтому не поддаются прямому измерению. Такие характеристики принято называть скрытыми или латентными. Для оценки латентных характеристик используются косвенные методы, в частности, анализ ответа на поставленные вопросы или анализ реакций на определенные стимулы. Вообще говоря, латентная переменная не есть какая-либо врожденная черта. Она может и должна меняться во времени вместе с личностью, например: способность читать, складывать числа, умение вычислять интегралы и т. п.
Важно отметить, что результаты тестирования зависят от многих факторов: условий проведения тестирования, мотивации испытуемых, их опыта работы с аналогичными тестовыми материалами и т. п. В данном случае мы не учитываем данные факторы и считаем, что при проведении повторного испытания тестируемый покажет те же самые результаты (значение латентной переменной не изменится). Это предположение существенно при анализе рассматриваемых математических моделей тестирования.
Таким образом, будем рассматривать латентную переменную θ как абстрактное математическое понятие, которое обозначает исследуемую характеристику личности. Множество всех возможных значений латентной переменной представим в виде одномерного или многомерного пространства, которое называется пространства, которое называется латентным пространством Ω.
Модели, в которых пространство Ω является одномерным, называются гомогенными.
Модели, в которых при анализе результатов тестирования рассматривается многомерное пространство Ω, называются гетерогенными.
Один из классических примеров латентного пространства - модель Бине-Симона [5], где в качестве латентной переменной рассматривается так называемый "умственный возраст".
В качестве другого примера укажем на подход Б.У. Родионова, А.О. Татура [51], которые представляют структуру латентного пространства в виде плоскости. По одной из осей откладывается объем учебной информации (знания), которой владеет тестируемый, а по другой оси - степень владения этой информацией (умения).
Примером использования многомерного латентного пространства (более 10 независимых латентных переменных) является широко известный психологический опросник MMPI [5].
Выбор структуры латентного пространства зависит от структуры информации, которую желает получить тесто-лог в результате тестирования. Построение латентного пространства - непростая задача, тесно соприкасающаяся с психологией и теорией познания.
Всюду далее, если не оговорено противное, будем предполагать, что латентное пространство одномерно.
Пусть Ω - латентное пространство и θ∈Ω. Для каждого дихотомического задания (задание называется дихотомическим, если ответ оценивается в бинарной шкале -верно/неверно). Через Р = Р(θ) обозначим вероятность правильного ответа испытуемого, для которого 9 есть истинное значение латентной переменной. Для политомических заданий (т. е. заданий, оцениваемых в многобалльной шкале [0, m]) Р(θ) отождествим с оценкой в отнормированной шкале оценивания [0, 1].
Монотонно неубывающая функция πi : Ω → [0,1] описывающая вероятность выполнения задания тестируемым с различным уровнем латентной переменной θ∈Ω πi(θj)=P(θj)=P(uij=1:θj), называется характеристической функцией i-го задания.
Характеристическая функция задания является монотонной, неубывающей и 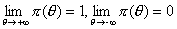 .
.
Испытуемый с большей латентной переменной θ2 имеет большую вероятность ответа, чем испытуемый с латентной переменной θ1(θ1<θ2).
Основная идея введения характеристических функций заданий состоит в том, что вероятность правильного ответа на задание и ошибка измерения связаны с латентной переменной в функциональной зависимостью. Можно сказать, что коэффициент решаемости - это усредненная характеристика задания.
Значение переменной θ, в
котором функция πi(θ)
равна 0,5, называется трудностью задания и обозначается
bi:πi(bi)=0,5.
Если такого значения переменной не существует (характеристическая
функция терпит разрыв), то трудностью задания bi
называется точка, в которой 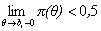 , но
, но 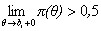 .
.
Множество заданий называется равномерно трудным, если для каждой пары заданий из этого множества их характеристические функции πi и πk удовлетворяют условию:
πi(θ)≤πk(θ), ∀θ∈Ω.
При этом задание с характеристической функцией πk(θ) называется более трудным, чем задание с характеристической функцией πi(θ).
Класс характеристических функций в модели Раша (см п. 3.3.3) является примером множества характеристических функций с равномерно трудными заданиями.
Пусть тест Т составлен из N заданий с характеристическими функциями πk(θ) (i=1,...,N). Функцию, равную среднему арифметическому характеристических функций заданий
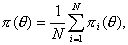
называют характеристической функцией теста Т.
Характеристическая функция π осуществляет преобразование латентного пространства Ω в шкалу результатов тестирования. Это преобразование, вообще говоря, не является линейным. Например, если все задания, составляющие тест, имеют одну и ту же характеристическую функцию, то характеристическая функция теста совпадает с характеристической функцией заданий. Если тест составлен из двух подмножеств заданий - легких и тяжелых, то на характеристической кривой будут ярко выражены три участка с различной степенью кривизны. Такой тест будет хорошо дифференцировать "слабых" и "сильных" учащихся, но плохо дифференцировать "средних". Кривая будет пологой в середине интервала изменения θ, но крутой на концах. Чем круче кривая, тем больше степень расслаивания.
Характеристическая функция π является полезным инструментом при конструировании теста. Можно сказать, что π осуществляет преобразование исходного распределения тестируемых в распределение результатов тестирования.
В [36] приведены примеры характеристических функций тестов с различной степенью расслаивания в предположении нормального распределения тестируемых.
3.3. Модели характеристических кривых.
Пусть при проведении тестирования используются задания, которые оцениваются в шкале [0, m]. Тогда с каждым заданием свяжем (m+1) - мерный вектор результате его использования (z0, z1,..., zm),
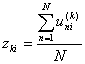
где u(k)ni - результат выполнения n-м тестируемым i-го задания, оцененного в k баллов, N - количество тестируемых.
По результатам выполнения задания тестируемые могут быть разбиты на
m+1 упорядоченную
(непересекающуюся) группу: G0,
G1,...,
Gm
- в группу Gk
попадают все тестируемые, выполнившие задание на k
баллов и имеющие латентные переменные 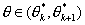 .
.
Функция 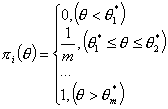 является характеристической функцией задания.
является характеристической функцией задания.
При использовании параметрических моделей задача состоит в подборе кривой из заданного класса, "наилучшим" образом описывающей данную параметрическую характеристическую кривую.
3.3.1. Нормальные модели.
С исторической точки зрения, естественно ожидать, что первый класс характеристических кривых, который был рассмотрен, основывался на идее нормального распределения. F. Lord [76, 77], используя идеи R. Fergusson, рассмотрел параметрические модели, в основе описания характеристических функций которых лежала функция
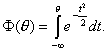
Говорят, что рассматривается трехпараметрическая нормальная модель, если для описания характеристических функций используется следующий класс кривых Фa,b,c(θ):
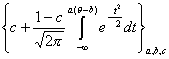
Числа a, b, c называют параметрами модели.
Параметр а называется дифференцирующей способностью задания.
Параметр b - трудностью задания и совпадает с точкой на шкале, в которой значение функции равно 0,5. Функция в этой точке имеет точку перегиба.
Параметр с называют коэффициентом угадывания.
Если используется класс кривых
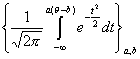
(т. е. c=0), то говорят, что рассматривается двухпараметрическая нормальная модель.
Если используется класс кривых
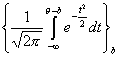
(т. е. с = 0, а = 1), то говорят, что рассматривается однопараметрическая нормальная модель.
В настоящее время изучение нормальных моделей представляет лишь теоретический интерес, поскольку их практическое использование затруднено вычислительными трудностями и наличием более практичных логистических моделей.
3.3.2. Логистические модели.
Для описания характеристических функций A. Birnbaum [64] предложил использовать более простые функции, получившие название логистических:
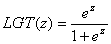 .
.
Дело в том, что, с практической точки зрения, функция Ф(z) и LGT(z) отличаются на всей числовой оси не более чем на 1% их значений, но, с математической точки зрения, существенно более просты в работе. Более того, опыт работы показал, что наибольшее количество новых идей и приложений связано именно с логистическими функциями.
По аналогии с нормальными моделями различают одно-, двух- и трехпараметрические модели. A. Birnbaum рассмотрел двух- и трехпараметрические модели. Однопараметрическую модель исследовал G. Rasch [79].
Опишем наиболее часто встречающиеся и используемые логистические модели характеристических кривых.
| Название моделей | Класс функции |
|---|---|
| однопараметрическая |
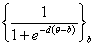 |
| двухпараметрическая |
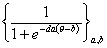 |
| трехпараметрическая |
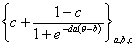 |
Параметры трехпараметрической логистической модели называются:
a - дифференцирующая способность задания;
b - трудность задания;
c - коэффициент угадывания.
Константа d обычно принимается равной 1,7.
Чем больше а, тем круче характеристическая кривая, т. е. больше дифференцирующая способность задания расслаивать тестируемых.
Чем больше b, тем больше трудность задания.
Коэффициент угадывания c обычно рассматривается в заданиях закрытого типа, где вероятность угадывания правильного ответа довольно существенна.
3.3.3. Модель Раша.
Датский математик Джордж Раш [79] независимо от исследований Лорда и Бирнбаума изучил частный случай трехпараметрической логистической модели Бирнбаума, в которой предполагал:
- все задания имеют одинаковый коэффициент селективности;
- коэффициент угадывания пренебрежимо мал.
В этом случае характеристическая функция задания может быть записана в виде:
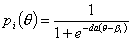 ,
,
где a - средний коэффициент селективности заданий.
В этом случае точкой перегиба характеристической функции является значение θ=βi Значение функции этой точке равно 0,5. Таким образом, в этой модели испытуемый со значением латентной переменной θ=βi ответит корректно на это задание с вероятностью, равной 0,5.
3.3.4. Модель Гутмана.
Guttman [66, 67] предложил в качестве характеристических функций дихотомических заданий использовав функции вида
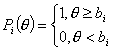 .
.
Можно сказать, что модель Гутмана является предельным случаем двухпараметрической логистической модели при a →∞.
3.4. Информационные функции.
Степень расслаивания тестируемых зависит от крутизны характеристической кривой.
Зависимость между информативностью задания и латентной переменной θ описывается информационной функцией задания. Информационной функцией называется функция
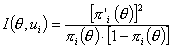 , (3.4.1)
, (3.4.1)
где πi(θ) - характеристическая функция задания ui, π’i(θ) производная этой функции.
В качестве примера рассмотрим вид информационных функций заданий, если их характеристические функции описываются логистическими кривыми. Подставляя в (3.4.1) конкретные значения πi(θ) для одно-, двух- и трехпараметрических логистических моделей, получим:
| Название моделей | Класс функции |
|---|---|
| однопараметрическая |
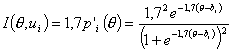 |
| двухпараметрическая |
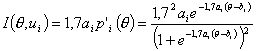 |
| трехпараметрическая |
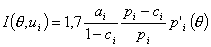 |
Нетрудно видеть, что для одно- и двухпараметрической логистической модели информационная функция принимает Максимально значение при аргументе, равном bi.
В трехпараметрической логистической модели экстремум информационной функции достигается [68] в точке
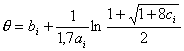
Информационной функцией тест-билета, состоящего из n дихотомических заданий, называется функция
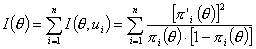 (3.4.2)
(3.4.2)
Информационная функция была введена A. Birnbaum в 1968 г. для оценивания эффективности каждого задания и тест-билета в целом. Основная идея - минимизировать ошибки измерения.
Если в классических моделях тестирования стандартная ошибка измерения не
зависит от θ и определяется в
"среднем", то в моделях IRT (Item
Responce Theory)
ошибка измерения является функцией от θ:
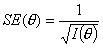
Следует отметить, что термин "информационная функция" не совсем удачен. Корректнее эту функцию можно было бы назвать функцией точности измерения.
Равенство (3.4.2) делает возможным эффективную процедуру конструирования тест-билета из отдельных откалиброванных заданий (т.е. заданий, статистические характеристики которых получены в результате пилотных испытаний).
Два тест-билета могут быть сравнимы с точки зрения их информационных функций.
Отношение информационной функции тест-билета T1 к информационной функции тест-билета Т2 называют относительной эффективностью (relative efficiency) тест-билета T1 по отношению к Т2.
Информационные функции заданий и тест-билета в целом - важное понятие в Item Responce Theory. Во-первых, с помощью этих понятий определяется стандартная ошибка измерения для каждого задания в зависимости от значения латентной переменной θ. (В этом существенное отличие современных подходов от классической теории тестирования, в которой стандартная ошибка измерения определяется "в среднем" для всех тестируемых). Во-вторых, информационные функции позволяют оценивать "вклад" каждого отдельного задания. Добавляя или удаляя задания, можно отслеживать эффективность тест-билета в целом как "измерительного устройства". Это свойство информационных функций делает их весьма удобным инструментом при конструировании тест-билетов.