В начало

Список литературы

Глава 6. Автоматизация проектирования тест-билетов.

6.1. Проблема проектирования тест-билетов.

Компьютерная генерация теста требует разработки математического аппарата, формально представляющего различные проблемы конструирования тестов в виде задач математического программирования. В работах, посвященных данной проблеме [37], рассматриваются подходы, позволяющие формализовать задачу конструирования тест-билета как задачу целочисленного математического программирования: найти решение, обеспечивающее оптимальное (максимальное или минимальное) значение целевой функции при заданных ограничениях на множестве возможных значений решения, при этом координаты вектора решения предполагается двузначным - 0 или 1.

Сопоставляя с тест-билетом вектор x с целочисленными координатами x_i=0∨1, значения которых определяют, включено или нет задание с номером i значения ее численно оценивали требуемое качество тест-билета (например, количество используемых заданий), а также задавая ограничения f_i(x)≤0 , например, на множество используемых заданий, приходим к следующей задаче целочисленного программирования:

min{Ф₀(x)/f_j(x)≤0, j=1,...,S; x_i=0∨1, i=1,...,N}

Вместе с тем, только простейшие случаи описываются с помощью одной целевой функции, значения которой измеряют качество решения тест-билета. В более сложных ситуациях качество решения не может быть оценено единственной целевой функцией. Таково положение дел при работе в многокритериальных ситуациях, например, когда конструктор должен учитывать качество нескольких параметров тест-билета.

В работе [37] предложена более общая математическая постановка задачи автоматизированного конструирования тест-билетов. Основой обобщения служит замена скалярной целевой функции Ф₀(x), оценивающей качество теста, на вектор-функцию оценок качества 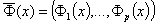и интерпретация "оптимального" решения в терминах функций выбора, порожденных бинарными отношениями R между значениями вектор-функции 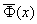на множестве альтернатив.

В такой постановке задача автоматизированного конструирования тест-билета формулируется как задача обобщенного математического программирования: найти решение, "лучшее" в смысле заданной конструктором функции выбора, среди всех, удовлетворяющих накладываемым ограничениям.

Список используемых обозначений:

N - общее количество файлов заданий в банке заданий. Все задания в одном файле заданий являются эквивалентными относительно имеющихся у них характеристик.

n∈1...N - номер файла заданий (или произвольного задания из файла) в банке заданий.

m - общее количество характеристик файла заданий.

A_n = (a_n1,a_n2,...,a_nm) - характеристический вектор n-го задания (файла заданий). Координаты вектора описывают множество характеристик задания (технологических, экспертных, статистических). Такими характеристиками, например, являются IRT-характеристики задания, время решения задания t_n, время представления мультимедиа информации t_n, тип задания

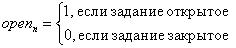
и ряд других.

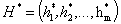- ограничения снизу, накладываемые на значения характеристик a_nl,...,a_nm задания.

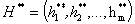- ограничения сверху на значения характеристик задания.

θ - значение латентных способностей испытуемых.

С - количество пробных точек на шкале значений θ.

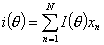- информационная функция теста.

I_n(θ) - информационная функция n-го задания.

x∈E^N, x=(x_l,x₂,...,x_N) - целочисленный вектор, координаты х_n, которого определяют, использовано ли задание из файла заданий n в конструируемом тесте: х_n={0,l}, х_n=1, если задание из файла n включено в тест, х=0 - если ни одно задание из файла n не используется в тесте.

X={x∈E^N|x=(x₁,x₂,...,x_N), x_n=0∨1} - множество всех целочисленных векторов с двузначными координатами. Каждый вектор х множества X определяет некоторый набор заданий для теста.

6.2. Постановка задачи автоматизированного проектирования тест-билетов.

Опишем обобщенную математическую модель проектирования тест-билета на основе оптимального выбора заданий из банка заданий.

Вектор А_n=(а_n1,а_n2,...,а_nm) описывает т характеристик m-го задания из банка заданий, где n∈l,...,N. Тогда, используя тензорное произведение векторов A_l,A₂,...,A_N на вектор х∈X, представим тест-билет Т в виде

T≡=T(x)=(x₁A₁,x₂A₂,...,x_NA_N).

Поскольку А_n является вектором, то Т идентифицируется с элементом тензорного произведения Е^м⊗X, которое изометрично (с естественно наследуемой топологией) подпространству пространства векторнозначных векторов E^NE^M.

На практике число N достаточно велико (порядка нескольких тысяч), и по мере разработки и включения в базу заданий новых тестовых заданий N→∞. Поэтому тест-билет можно рассматривать как точку в пространстве бесконечномерных последовательностей .

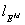Качество проектируемого тест-билета Т(х) в каждой точке x∈X оценивается вектор-функцией

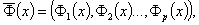
где Р - количество локальных критериев,

Ф_Р(х) - функции оценивания локальных критериев тест-билета.

Например, приняв в качестве локального критерия количество заданий в тест-билете, можно построить следующую функцию оценивания:

.

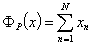Ниже указаны примеры некоторых других функций оценивания.

Кроме того, при проектировании тест-билета вводятся дополнительные ограничения как на характеристики тест-билета в целом, так и на параметры тестовых заданий. Обозначим через S количество всех ограничений. В общем случае ограничения можно записать в виде

f_s(x)≤0, s=1,...,S

рассматривая, при необходимости, ограничения - равенства как два неравенства.

Приведем в качестве примера ограничение на общее время решения теста:

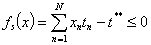
Проблема конструирования тест-билета [37] была сформулирована как задача целочисленного математического программирования: вычислить вектор х^*∈X, удовлетворяющий заданным ограничениям и доставляющий максимум (или минимум) заданной функции оценивания локального критерия Ф_Р(х):

max{Ф_Р(х)|х∈X, f_s(x)≤0, s=l,...,S}.

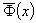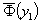Рассмотрим более общую постановку задачи автоматизированного проектирования тест-билета, перейдя от скалярной функции оценивания критерия Ф_Р(x) к вектор-функции , интерпретируя оптимизацию в терминах некоторых бинарных отношений R между элементами и 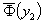, y₁, y₂∈X. В такой постановке задача может быть сформулирована как задача обобщенного математического программирования: требуется вычислить вектор х^*∈X, такой, что

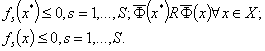
Тогда тест-билет Т(x^*) является лучшим относительно значений вектор-функции 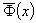на множестве всех объектов Т(х), х∈X, удовлетворяющих ограничениям

f_s(x)≤0, s=1,...,S.

При этом понятие "лучший" интерпретируется в терминах заданного бинарного отношения R. Приведем в качестве примера бинарное отношение R, реализующее вычисление элемента х^*, являющегося решением указанной выше задачи целочисленного программирования - максимизации скалярной функции Ф_P(x):

Ф_P(x)R Ф_P(y)⇔ Ф_P(x)≥ Ф_P(y).

Тогда, если, x^*∈X, f_s(x^*)≤0, s=1,...,S и

Ф_P(x^*)RФ_P(y)∀y∈X:f_s(y)≤0, s=1,...,S⇔ Ф_P(x^*)≥ Ф_P(y)∀y∈X:f_s(y)≤0, s=1,...,S,

т.е. x^* является решением данной задачи.

Бинарное отношение R является механизмом, реализующим некоторую функцию выбора. Через заданное выше бинарное отношение "больше или равно" реализована функция выбора лучшего по заданному скалярному критерию качества Ф_Р(x) варианта х^*∈X при заданных ограничениях (скалярный оптимизационный механизм).

Приведем несколько примеров функций выбора, отвечающих различным механизмам принятия решений на основе значений вектор-функции оценок качества тест-билета :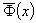

1. паретовский механизм (рис. 6.1):

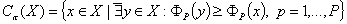
Данный механизм позволяет сократить множество исходных вариантов, то есть исключить из неформального анализа те варианты решений, которые заведомо будут плохи. Принцип Парето не выделяет единственного решения, а только сужает множество альтернатив. Окончательный выбор остается за лицом, принимающим решение;

Рис. 6.1. Дуга ABC - множество Парето.

2) механизм лексикографической оптимизации, определяемый вектор-функцией критериев, упорядоченных по важности:

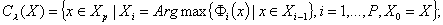
3) механизм голосования (выбор по большинству):

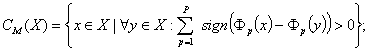
4) введение метрики в пространстве целевых функций (рис. 6.2).

Если известны величины

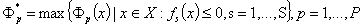, доставляющие максимальные значения частным критериям, то можно определить множество 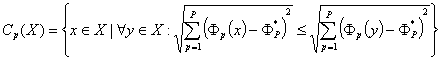- ближайших по евклидовому расстоянию к точке "абсолютного максимума" 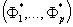точек 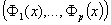в пространстве критериев. Множество С_р(х) показывает предельные возможности достижения "абсолютного максимума".

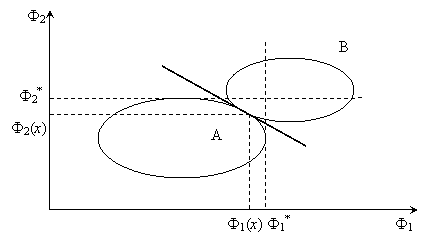
Рис. 6.2. Точка А - ближайшая к точке "абсолютного максимума" В.

Указанные выше функции выбора можно представить как функции выбора, определяемые бинарными отношениями R_π, R_λ, R_M, R_P,где

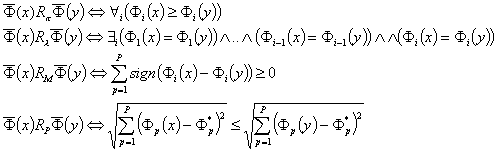
Поиск оптимального решения проводится в виде последовательных процедур:

• формируется вектор-функция оценок значений критериев тест-билета и множество ограничений из предлагаемого конструктору теста списка;
• конструктор задает функцию выбора и соответствующее ей бинарное отношение R;
• рассчитывается множество решений (тест-билетов), лучших относительно заданной функции выбора;
• в интерактивном режиме проводится доработка тест-билета до полного удовлетворения требованиям конструктора теста.

Ниже описаны вычислительные аспекты алгоритма решения задачи обобщенного математического программирования.

6.3. Примеры математических моделей конструирования тестов.

Рассмотрим примеры функций оценки критериев тест-билета и функций-ограничений, а также постановки некоторых задач автоматизированного проектирования тест-билетов в виде задач целочисленного математического программирования.

В качестве функций оценки критериев могут быть использованы:

• количество заданий в тест-билете:

,

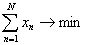• время решения тест-билета:

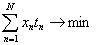где t_n - время решения задания,

• значения информационной функции в заданных точках θ_c на шкале латентных способностей испытуемого:

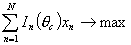
• приближение к заданной форме информационной кривой теста:

λ→max, где λ. - наибольшее вещественное число, для которого выполняется

.

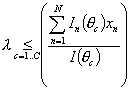Ниже приведены примеры накладываемых ограничений:

• на коэффициент надежности тест-билета:

n≤n^*,

• значения информационной функции в заданных точках θ_c:

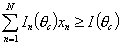
• общее время решения теста:

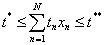
• число задании в тесте:

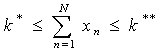
• число учебных элементов р:

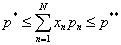
• обязательное использование некоторого задания n в тесте:

x_n=1,

• исключение некоторого задания n из теста:

x_n=0,

• необходимое для печати теста количество бумаги l:

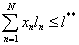
• минимально достаточный объем носителей для использования данного теста (при компьютерном тестировании):

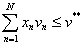
• использование только открытых (закрытых) задании:

open x_n=1 ((1-open)x_n=1),

• использование задании, допускающих компьютерное представление:

comp_n=1,

• использование заданий, допускающих бумажное представление:

papir_n=1.

• использование заданий определенных уровней усвоения α:

α^*≤α_n≤α^**

• использование заданий определенных ступеней абстракции β:

β^*≤β_n≤β^**

• использование заданий определенных степеней осознанности τ (τ^* ≤ τ_n ≤ τ^**):
• с ограничением на время выполнения задания t

t^*≤t_n≤t^**

• с ограничением на коэффициент решаемости задания k

k^*≤k_n≤k^**

• с определенным коэффициентом селективности задания r

r^*≤r_n≤r^**

• с заданной трудностью задания b

b^*≤b_n≤b^**

• с дифференцирующей способностью задания а

a^*≤a_n≤a^**

Приведем простейшие примеры описанной в предыдущем разделе общей модели конструирования тест-билета. Все примеры сводятся к задаче целочисленного программирования со скалярной целевой функцией и минимальным количеством ограничений:

1) конструирование теста фиксированной длины с максимальной информационной функцией, ограниченной снизу [61, 62, 65]:

,

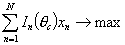при ограничениях

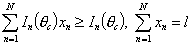где l - заданная длина теста;

2) конструирование теста минимальной длины при фиксированной нижней границе информационной функции [62]:

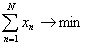
при ограничениях ;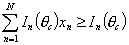

3) конструирование теста фиксированной длины с максимальной информационной функцией заданной формы [61]:

λ→max, где λ - наибольшее вещественное число, для которого выполняется

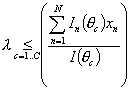и 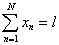, где l - длина теста.

В данном случае пороговые значения информационной функции теста I(θ_c) трактуются как весовые коэффициенты, с помощью которых задается форма информационной кривой.

6.4. Вычислительные аспекты задачи автоматизированного проектирования тест-билетов.

Задача автоматизированного проектирования тест-билета Т(х) была сформулирована выше как задача обобщенного математического программирования (ЗОМП):

найти

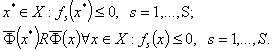
Рассмотрим основные идеи методов решения данной задачи, комбинирующие в себе версии методов центров тяжести и методов эллипсоидов [34]. Эффективность данных вычислительных методов аргументируется соответствующими формальными рассуждениями и подтверждается при тестировании на разнообразных классах задач [37].

Для решения ЗОМП указанными методами следует предварительно представить ее область определения в некотором стандартном, удобном для анализа виде (шар, эллипсоид). Стандартная исходная ситуация позволяет на первом шаге существенно улучшить значение целевого функционала. После первого шага ситуация меняется: область локализации решения сокращается и теряет свою стандартную форму. Переход ко второму шагу начинается с некоторого преобразования координат, которое придает области локализации исходную стандартную форму, удобную для очередного улучшения значения целевого функционала.

Введем следующие обозначения:

D - верхняя оценка диаметра множества ,

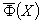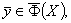
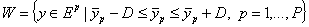- замкнутое множество, содержащее область изменения 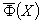x∈X,

X_f={x∈X | f_s(x)→£0, s=1,...,S} - допустимая область,

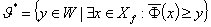- множество векторов x из допустимой области, для которых существует образ ,

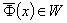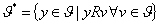- множество лучших относительно предпочтения R векторов y∈W, для которых определен прообраз x∈X_f.

Предполагается, что все определяющие задачу функции непрерывны на выпуклой оболочке X, а выпуклая оболочка множества X_f имеет непустую внутренность. В этих обозначениях множество решений ЗОМП определяется формулой .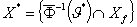

Пользуясь введенными обозначениями, запишем формулировку ЗОМП в следующем виде:

требуется найти точку у^*∈Θ^*; кроме того, найдя ее, необходимо построить 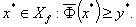Решение этой системы неравенств оказывается одним из решений ЗОМП.

Приведем теперь общую схему решения ЗОМП. Начнем решение с вычисления центра тяжести y₁=y₁(W₀), W₀=W. Заметим, что множество W₀-||.||_∞ - шар. Чтобы установить, принадлежит ли у₁ области Θ, необходимо решить следующую систему неравенств:

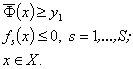
При этом могут возникнуть два случая: система неравенств несовместна или имеет решение. В первом случае строится линейный функционал (р, задающий гиперплоскость, отделяющую у₁ от Θ:

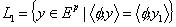. На следующей итерации, которая строится по тому же принципу, роль W₀ будет играть множество

.

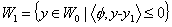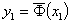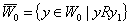Если же система неравенств имеет решение x₁, то находим ξ₀ -ненулевой опорный функционал к предпочтению R в точке , т.е. опорный функционал к множеству . Функционал ξ₀ определяет опорную гиперплоскость к множеству 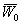в точке у₁. Полагаем 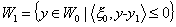- пересечение множества W₀ и полупространства векторов задаваемому ξ₀.

Переходим к следующей итерации, в которой роль у₁, играет y₂=y₂(W₁) - центр тяжести множества W₁. При этом каждая итерация процесса решения задачи позволяет перейти от области W_i-1 локализации решения к области W_i меньшего объема: |W_i|≤ω|W_i-1|, где |ω|≤1. Последовательное применение итерационной процедуры стягивает области допустимых планов к ε-окрестности решения ЗОМП, при этом точность ε получаемого решения задается пользователем.

Укажем основные вычислительные подзадачи, которые возникают на каждой k-й итерации метода (k=0, 1, 2,...).

Задача построения опорных функционалов ξ₀ и χ ко множествам 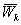и W_k является задачей линейного математического программирования:

найти ,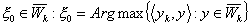

найти .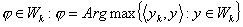

Для решения этих задач могут использоваться варианты симплекс-метода [34].

Для решения целочисленной системы неравенств

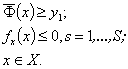
применяются методы, основанные на идеях методов ветвей и границ, подробно изложенных в [34].

Задача вычисления центра тяжести y_k=y_k(W_k-1) множества W_k-1, в общем случае имеющего произвольную структуру, является достаточно сложной. Поэтому используется подход, применяемый в методах эллипсоидов: каждая итерация начинается с вычисления эллипсоида минимального объема, содержащего в себе полусферу, полученную пересечением сферы W_k-1 и полупространства, отсекаемого гиперплоскостями L или L₁ . Данная задача является задачей квадратичного программирования. Затем, используя линейные преобразования, данный эллипсоид преобразуется в сферу равного объема. Указанная задача допускает явное решение. Формулы преобразования центра и радиуса сферы W_k-1 в сферу W_k можно найти в [34].

Таким образом, вспомогательные подзадачи, используемые на итерациях метода, являются стандартными в математическом программировании и имеют эффективные методы решения.

На основе описанной теоретической базы в МарГТУ реализованы программные комплексы для автоматизированного проектирования тест-билетов [57].