В начало

Список литературы

Глава 5. Модели и алгоритмы проектирования тестов.

5.1. Базовая модель.

Иногда эту процедуру называют неформальной (интуитивной, естественной, учительской), а созданные тест-билеты - неформальными (учительскими). Это объясняется тем, что тест-билеты по данной процедуре готовятся педагогами, исходя из своего большого опыта и для своих нужд. Эти тест-билеты, как правило, отличаются высокой степенью валидности, но, к сожалению, невысокой степенью надежности и других статистических характеристик. Данная процедура не требует специальных знаний теории тестирования и довольно проста в освоении.

Опыт показывает, что можно резко повысить эффективность создания учительских тест-билетов, если пользоваться некоторыми простыми инструментами. В качестве таких инструментов удобно использовать [36]:

• карту Шухарта коэффициентов решаемости (трудности) заданий;
• гистограмму пилотных результатов тестирования;
• диаграмму Парето коэффициентов решаемости заданий.

Коэффициент решаемости k - статистический параметр задания, который определяется в результате пилотных испытаний (предтестирование) на группе испытуемых, близкой по уровню тех, для кого готовятся тест-билеты. Для дихотомических заданий k определяется по формуле

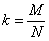, (5.1.1)

где N - количество решавших задание, М - количество решивших задание.

Для политомических - по формуле:

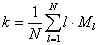(5.1.2)

где N - количество решавших задание,

М_l - количество решивших данное задание с оценкой, равной l,

l - оценка задания.

Ясно, что коэффициент решаемости задания 0 ≤ k ≤ 1. Если k близко к нулю, то задание тяжелое - его почти никто не решает. Если k близко к единице, то задание легкое - его выполняют почти все. С точки зрения составителя тест-билета эти задания не представляют интереса, поскольку практически ничего не проверяют.

Структуру решаемости заданий в тест-билете удобно представить в виде так называемой карты Шухарта: по оси абсцисс откладываются номера заданий, составляющих тест-билет, а по оси ординат - их коэффициенты решаемости. Пунктирные линии разделяют карту Шухарта на три зоны: зона легких заданий, зона средних заданий и зона тяжелых заданий. Большая часть заданий должна находиться в средней части. Однако небольшая доля заданий может находиться в нижней (часть заданий должны выполнить почти все) и верхней (задания для наиболее способных испытуемых) зонах.

Второй удобный инструмент визуализации - гистограмма результатов пилотных испытаний.

Гистограмма - удобный инструмент при сравнении результатов тестирования, полученных на различных группах испытуемых с помощью одного и того же тест-билета.

Таким образом, в базовой модели в качестве основной характеристики выступает коэффициент решаемости, а в качестве целевой функции (если можно так сказать) - форма гистограммы результатов тестирования.

Базовую (естественную, интуитивную) процедуру можно рассматривать как первый шаг в итерационном процессе создания качественного тест-билета по более сложным методикам.

5.2. Модель В.П. Беспалько.

Тест-билет представляет собой совокупность блоков тестовых заданий (тест-лестница) описываемых экспертными характеристиками (параметрами) α, β, и γ. В.П. Беспалько предлагает [10-13] следующую классификацию этих характеристик:

- параметр α - уровень усвоения знаний:

α =1 - узнавание (воспроизведение знаний с помощью извне),

α =2 - воспроизведение усвоенных знаний в типовых заданиях,

α =3 - применение знаний в практической деятельности,

α =4 - творчество;

- параметр β - ступень абстракции:

β=1 - феноменологическая (внешнее, описательное изложение явлений; каталогизация объектов, констатация их свойств и качеств);

β=2 - предсказательная, аналитико-синтетическая (элементарное объяснение природы и свойств объектов, закономерностей явлений);

β=3 - прогностическая, аналитическая (объяснение явлений с созданием их количественной теории, моделирование основных процессов, аналитическим представлением их законов и свойств);

β=4 - аксиоматическая, аналитическая (объяснение явлений с использованием высокой степени абстракции на базе сложного математического или логического формализма, обладающего большой обобщенностью описания);

- параметр γ - степень осознанности усвоения знаний:

γ=1 - первая ступень осознанности (при аргументации выполнения заданий используется только информация из изучаемого предмета);

γ=2 - вторая ступень осознанности (при аргументации выполнения заданий используется информация из близких по объекту изучения предметов);

γ=3 - третья ступень осознанности (при аргументации выполнения заданий используются широкие межпредметные связи из различных дисциплин).

Кроме параметров α, β, и γ В.П. Беспалько выделяет и параметр r - степень автоматизации деятельности.

Учащийся считается справившимся с данным уровнем, если он выполнил не менее 70% заданий из блока.

При конструировании тест-билета важное значение имеет определение априорной надежности тест-билета. Полагают, что она должна быть не менее 0,75. В.П. Беспалько предложил определять априорную надежность тест-билета, исходя из количества учебных элементов (существенных операций в его терминологии). Такой подход весьма удобен на первом этапе конструирования тест-билета, когда нет еще достаточной статистики для вычисления коэффициента надежности статистическими методами.

Под учебным элементом (существенной операцией) понимается элемент выполнения задания, без использования которого невозможно получить верное решение.

Установлено, что для априорной надежности тест-билета не менее 0,75 необходимо, чтобы он состоял из 40-60 учебных элементов.

Таким образом, можно сказать, что в модели В.П. Беспалько:

• целевые функции:

надежность R → max,

валидность V → max,

• основные характеристики:

уровень усвоения α,

ступень абстракции β,

степень осознанности усвоения знаний γ.

5.3. Классическая процедура.

С точки зрения классического подхода тест-билет, как и любой социологический инструмент измерения, должен удовлетворять свойствам высокой степени объективности, надежности и валидности.

Таким образом, в качестве критерия конструирования тест-билета выступают:

надежность → max,

валидность → max,

Объективность должна обеспечиваться процедурой организации тестирования.

В качестве основных статистических параметров заданий выступают:

k - коэффициент решаемости задания (трудность),

D - коэффициент селективности.

Результат тестирования можно представить в виде суммы:

Х = Т + Е, (5.3.1)

где Т - истинное значение латентной переменной тестируемого,

Е - ошибка измерений.

Распределение этих переменных, как правило, неизвестно.

Если тест-билет составлен из дихотомических заданий, то истинное значение:

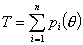, (5.3.2)

если политомических, то

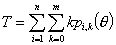(5.3.3)

Надежность теста 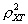определяется как квадрат корреляции между результатом и истинным значением тестирования и может быть записана как

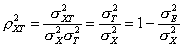, (5.3.4)

где σ_XT - коэффициент корреляции X и Т,

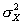- дисперсия распределения результатов тестирования,

- дисперсия распределения латентной переменной,

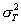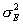- дисперсия распределения ошибки измерения.

Нетрудно видеть, что надежность теста равна единице, если .

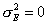Такое определение надежности представляет теоретический интерес, но на практике его использование невозможно. Одна из самых распространенных процедур практического нахождения надежности была разработана в работе [73].

С другими процедурами можно ознакомиться по работам [5, 66].

Из различных формул, приведенных в [73], для вычисления коэффициента надежности тестов, составленных из дихотомических заданий, наиболее часто используется формула:

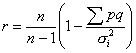(5.3.5)

Если тест-билет составлен из политомических заданий, то в качестве коэффициента надежности обычно используют коэффициент альфа:

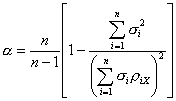(5.3.6)

где n - число заданий в тест-билете,

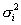- дисперсия i-го задания,

ρ_iX - коэффициент корреляции между i-м заданием и тест-билетом.

Таким образом, в классической модели:

целевая функция:

коэффициент надежности R → max,

основные характеристики:

коэффициент решаемости k,

коэффициент селективности D.

Отметим, что параметры k и D зависят от конкретной популяции тестируемых и могут эффективно использоваться лишь для аналогичной популяции.

5.4. Модель Лорда-Бирнбаума.

В этой модели в качестве критерия построения тест-билета рассматривается максимизация количества информации, которое можно получить о тестируемом (с уровнем θ=θ₀). Согласно [64] под "количеством информации", которое получается при включении в тест-билет i-го задания, понимается величина, обратно пропорциональная стандартной ошибке измерения данного значения θ₀ с помощью i-го задания.

Процедуру можно представить из следующих шагов:

1. строится целевая информационная функция,
2. из банка заданий последовательно выбираются задания таким образом, чтобы коэффициент трудности b_i был как можно ближе к значениям θ, при которых достигается максимум целевой информационной функции,
3. после каждого добавления следующего задания (пере)вычисляется информационная функция тест-билета,
4. процедура продолжается до тех пор, пока информационная функция тест-билета не аппроксимирует с достаточной степенью целевую информационную функцию.

Весьма полезной при конструировании тест-билета может оказаться процедура сравнения информационных функций различных версий тест-билета (добавляя или убирая задания различной степени трудности).

Таким образом, в модели Лорда-Бирнбаума:

целевая функция: информационная функция J(θ):

|J(θ)-J_ц(θ)|→min,

основные характеристики: параметры логистических кривых:

a - дифференцирующая способность,

b - трудность,

c - коэффициент угадывания.

5.5. Процедура B.C. Аванесова.

Для минимизации процедуры определения уровня подготовленности тестируемого B.C. Аванесов предложил при конструировании тест-билета располагать тестовые задания в порядке возрастания их трудности: "Педагогический тест-это система фасетных (откалиброванных) заданий определенного содержания, возрастающей трудности, специфической формы, позволяющая качественно оценить структуру и эффективно измерить уровень знаний, умений, навыков и представлений" [2], что эквивалентно убыванию коэффициентов решаемости.

Метод удобен для визуализации расположения в тест-билете заданий различной степени трудности. Однако, необходимо следить за тем, чтобы задания покрывали шкалу логитов достаточно плотно. В противном случае может образоваться большая группа тестируемых, результаты которых не различимы.

Таким образом в модели B.C. Аванесова:

целевая функция: порядок расположения заданий u_i таким образом, чтобы b_i≤b_i+1;

основные характеристики: трудность задания b_i.

5.6. Многоцелевая модель.

В связи с появлением компьютерных систем конструирования тест-билетов [29, 37] появляется возможность разработки многофункционального тест-билета с использованием различных моделей. Выбор конкретных характеристик при конструировании тест-билета зависит от целей тестирования, а именно - какую информацию желает получить тестолог в результате педагогических испытаний.

При конструировании тест-билета с помощью много-Целевой процедуры используется секвенциальный подход, т.е. последовательное приближение к целевым установкам (функциям) путем пошагового добавления (изменения, удаления) тестовых заданий.

Опишем алгоритм процедуры:

1) определение (задание) области валидности тестирования.

Этот этап заключается в построении дерева целей тестирования и выборе из банка заданий баз заданий, которые соответствуют выбранной области валидности и из которых будут выбираться тестовые задания,

2) выбор интерпретационной системы для последующего анализа результатов тестирования.

Если для анализа будет использоваться метод уровней, то предварительно производится вербальное описание каждого из уровней. При включении в тест-билет нового задания отмечается уровень, для описания которого оно будет использоваться,

3) выбор предполагаемого профиля гистограммы и определение набора "трудностей" тестовых заданий:

- выбирается предполагаемый профиль гистограммы и выдвигается гипотеза о "среднем уровне обученности" М и размахе уровня обученности W.

При экспертном оценивании М и W может помочь опыт построения аналогичных тест-билетов, экспертная оценка уровня подготовленности учащихся и т.п. Бывает полезно предварительно ознакомиться с заданиями из базы заданий и, основываясь на известных параметрах заданий, предугадать возможный уровень ответов и, следовательно, возможный уровень заданий, с которыми справятся (не справятся) обучаемые.

- полагают среднеквадратичное отклонение

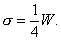
В силу неравенства Чебышева интервал (M-2σ, M+2σ) должен содержать 75% тестируемых, а если предполагаемое распределение нормально, то более 95%,

- вычисляется предполагаемая длина тест-билета

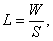
где S - стандартная ошибка измерений, оцененная каким-либо образом,

- интервал 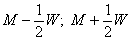разбивается на L равных интервалов. Задания из базы заданий выбираются таким образом, чтобы их трудность принадлежала одному интервалу и так, чтобы каждому интервалу соответствовало по крайней мере одно задание.

4) определение целевой информационной функции и определение степени приближения к ней.

Предварительно задается целевая информационная функция. По мере добавления в тест-билет новых заданий производится визуальное сравнение двух функций.

5.7. Модульно-матричные модели.

Часто возникает задача об определении уровня подготовки не отдельного учащегося, а целой категории. Например:

- установление эффективности качества образования учебного заведения в целом требованиям государственного образовательного стандарта,

- определение эффективности образовательных программ,

- установление уровня подготовки в образовательном учреждении при его аттестации и аккредитации.

В этих случаях довольно эффективный и дешевыми являются модульно-матричные процедуры проведения тестирования.

Пусть для проведения тестирования по какому-либо учебному предмету с помощью одной из процедур, описанных выше, разработан тест-билет Т. Идея модульного метода состоит в том, чтобы разбить этот тест-билет на ряд подтест-билетов (модулей) T₁, Т₂,..., T_k таким образом, чтобы каждый учащийся отвечал не на весь тест-билет Т, а лишь на его часть T_i (экономя при этом время и ресурсы), но так, чтобы в совокупности относительно данной категории учащихся были получены такие же результаты, как и при предъявлении целого теста Т.

Алгоритм такого разбиения может быть следующим:

1) строим диаграмму Парето по параметру трудности заданий (или, что эквивалентно, по параметру коэффициента решаемости),

2) задания разбиваются на блоки по n заданий в каждом,

3) подтест-билет T₁, составляется таким образом, чтобы из первого блока было выбрано самое легкое задание, из второго - второе по трудности и т. д. Соответственно в Т₂ войдут задания: из первого блока - второе по трудности, из второго блока - третье по трудности и т. д. Такая компоновка позволяет формировать подтесты примерно одинаковой трудности,

4) полученная совокупность подтест-билетов T₁,T₂,...,T_k является искомой.

5.8. Общая схема проектирования тестов.

Рассмотрим основные этапы создания тестовых материалов.

1. Постановка целей педагогических измерений. Перед началом разработки тестов необходимо четко определить, с какой целью проводится тестирование, поскольку именно цель определяет содержательную и качественную сторону нижеследующих этапов. Целью педагогического измерения может быть:

• индивидуальная диагностика-оценка обученности отдельного учащегося, определение профессионального уровня работника системы образования,
• массовая диагностика - оценка обученности популяции учащихся (школьный класс, студенческая группа, образовательная организация в целом и т.п.),
• задача отбора (например, при приеме в учебное заведение или переводе на следующий уровень обучения),
• задача селекции (например, определение победителей олимпиады или кандидатов на обучение по индивидуальной программе),
• задача оценки эффективности образовательной программы или методики обучения.

2. Определение и выбор подходящей модели проектирования тестов.

Так, если цель педагогического измерения - оценка уровня обученности, то проектируемые тесты должны содержать задания (точнее контролируемые учебные элементы) из наибольшего количества учебных тем. Статистическое распределение результатов измерений в этом случае близко к нормальному.

Если цель измерения - отбор учащихся, то тесты должны содержать "норму-минимум", выполнение которой позволяет обучаемому, прошедшему отбор, успешно учиться дальше. Максимальное значение статистического распределения в этом случае будет смещено вправо.

Если цель измерений - селекционная, то тесты должны содержать задания с высоким уровнем усвоения, ступенью абстракции и степенью осознанности. Поэтому лишь немногие выполнят достаточно большое число заданий. Максимальное значение статистического распределения в этом случае будет смещено влево.

Если целью измерений является оценивание образовательных программ, то в этом случае экономнее использовать выборочные методы (например, модульно-матричную модель).

3. Подготовка (выбор существующего или создание собственного) банка откалиброванных заданий. Наиболее трудоемкий (и, следовательно, дорогой) этап в процедуре разработки тестов.

4. Создание структуры тестов. Определение валидности. Под структурой тестов понимают структурированный перечень названий файлов тестовых заданий с описывающими их характеристиками (и, в первую очередь, перечнем контролируемых учебных элементов). Обычно создание структуры производится вручную либо за экраном дисплея с помощью программного комплекса.

После создания структуры можно экспертно определить содержательную валидность тестов. Напомним, что под валидностью понимается соответствие между тем, что измеряется, и тем, что должно измеряться, т.е. степенью достижения тестами поставленных целей и отсутствием факторов, искажающих результаты измерения.

5. Проектирование тестов. Генерация необходимого количества вариантов. После того, как определена структура, производится проектирование тестов в соответствии с заданными целями.

6. Рецензирование и редактирование тестовых материалов являются следующим этапом проверки качества тестовых заданий. Оно может проходить в форме простого обсуждения членами рабочей группы и в форме внешнего (независимого) рецензирования.

Рецензия внешних экспертов должна, как минимум, содержать оценку:

• соответствия тестовых материалов поставленным целям,
• правильности выделения контролируемых учебных элементов,
• технических качеств заданий: краткость, ясность, отсутствие двусмысленностей, искусственных сложностей, подсказок,
• единства стиля, единообразия формы и соответствия текстов заданий нормам языка,
• качества тестов в целом.

7. Пилотное испытание - важный этап в разработке тестов. Оно призвано определить его валидность и надежность, отбраковать неудачные задания. Пилотное (пробное) испытание проводится, как правило, на относительно небольших группах (хотя, с точки зрения накопления статистики, чем больше, тем лучше) для того, чтобы:

• определить первичные статистические характеристики заданий и материалов в целом,
• оценить возможность использования тестов для измерения тех характеристик, которые предусмотрены целями педагогического измерения,
• выполнить корректировку заданий на основе анализа результатов пробного испытания.

8. Анализ и коррекция. После пилотных испытаний Может оказаться, что полученные результаты не (полностью) соответствуют поставленным целям. Может оказаться, что характеристики тестовых заданий, полученные на Других выборках, не совпадают с полученными характеристиками. В этом случае необходима корректировка структуры тестовых материалов и набора заданий.

9. Оформление тестовых материалов включает в себя распечатку подготовленных вариантов, описания всех используемых характеристик, описания методики проведения педагогических измерений с использованием данного комплекса, методов оценивания заданий и методов интерпретации результатов измерений.

10. Сертификация тестовых материалов. Если предполагается, что тестовые материалы будут использоваться не только разработчиком в повседневной учительской практике, но и для нужд аттестации образовательных программ, то он должен удовлетворять ряду определенных (и достаточно жестких) требований, обеспечивающих возможность решать следующие задачи:

• проверять соответствие уровней обученности учащихся требованиям государственных образовательных стандартов,
• обеспечить возможность сравнения уровней обученности учащихся, проходящих подготовку по одинаковым образовательным программам в различных образовательных организациях.

Под сертификацией тестовых материалов понимается признание того, что данный комплект тестовых материалов позволяет решать перечисленные задачи.