Раздел I. Методические рекомендации к выполнению статистических расчетов
Раздел II. Образец выполнения и оформления заданий 1-3 курсовых и контрольных работ
Задание 2
По исходным данным табл. 1 с использованием результатов выполнения задания 1 необходимо выполнить следующее.
1. Установить наличие и характер корреляционной связи между признаками Объем кредитных вложений и Сумма прибыли, образовав по каждому признаку четыре группы с равными интервалами, используя методы:
а) аналитической группировки;
б) корреляционной таблицы.
2. Оценить тесноту корреляционной связи, используя коэффициент детерминации и эмпирическое корреляционное отношение.
Сделать выводы по результатам выполнения задания 2.
Выполнение задания 2
Целью выполнения данного задания является выявление наличия корреляционной связи между факторным и результативным признаками, установление направления связи и оценка ее тесноты.
Факторный и результативный признаки либо задаются в условии задания, либо определяются путем проведения предварительного теоретического анализа. Лишь после того, как выяснена экономическая сущность явления и определены факторный и результативный признаки, приступают к проведению корреляционного анализа данных.
По условию задания 2 факторным является признак Объем кредитных вложений (X), результативным - признак Сумма прибыли (Y).
1. Установление наличия и характера связи между признаками Объем кредитных вложений и Сумма прибыли методами аналитической группировки и корреляционной таблицы
1а. Применение метода аналитической группировки
При использовании метода аналитической группировки строится
интервальный ряд распределения единиц совокупности по факторному признаку
X и для каждой j-й группы ряда определяется среднегрупповое
значение 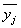 результативного признака
Y. Если с ростом значений фактора X от группы к группе
средние значения
результативного признака
Y. Если с ростом значений фактора X от группы к группе
средние значения 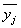 систематически
возрастают (или убывают), между признаками Х и Y имеет место
корреляционная связь.
систематически
возрастают (или убывают), между признаками Х и Y имеет место
корреляционная связь.
Используя разработочную таблицу 3, строим аналитическую группировку, характеризующую зависимость между факторным признаком X - Объем кредитных вложений и результативным признаком Y — Сумма прибыли. Макет аналитической таблицы имеет следующий вид (табл. 7):
Таблица 7
Зависимость суммы прибыли банков от объема кредитных вложений
| Номер группы | Группы банков по объему кредитных вложений, млн руб. | Число банков | Сумма прибыли, млн руб. | |
|---|---|---|---|---|
| всего | в среднем на один банк | |||
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| Итого | ||||
Групповые средние значения
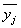 получаем из табл. 3 (графа 4), основываясь
на итоговых строках «Всего». Построенную аналитическую группировку представляет
табл. 8.
получаем из табл. 3 (графа 4), основываясь
на итоговых строках «Всего». Построенную аналитическую группировку представляет
табл. 8.
Таблица 8
Зависимость суммы прибыли банков от объема кредитных вложений
| Номер группы | Группы банков по объему кредитных вложений, млн руб., x | Число банков, fj | Сумма прибыли, млн руб. | |
|---|---|---|---|---|
| всего | в среднем на один банк, 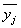
|
|||
| 1 | 40-90 | 3 | 50,4 | 16,800 |
| 2 | 90-140 | 6 | 241,3 | 40,217 |
| 3 | 140-190 | 12 | 711,4 | 59,283 |
| 4 | 190-240 | 9 | 704,0 | 78,222 |
| Итого | 30 | 1707,1 | 56,900 | |
Вывод: Анализ данных табл. 8 показывает, что с увеличением объема кредитных вложений от группы к группе систематически возрастает и средняя прибыль по каждой группе банков, что свидетельствует о наличии прямой корреляционной связи между исследуемыми признаками.
1б. Применение метода корреляционной таблицы
Корреляционная таблица представляет собой комбинацию двух рядов распределения. Строки таблицы соответствуют группировке единиц совокупности по факторному признаку X, а графы - группировке единиц по результативному признаку Y. На пересечении j-й строки и k-й графы указывается число единиц совокупности, входящих в j-й интервал по факторному признаку и в k-й интервал по результативному признаку. Концентрация частот около диагонали построенной таблицы свидетельствует о наличии корреляционной связи между признаками. Связь прямая, если частоты располагаются по диагонали, идущей от левого верхнего угла к правому нижнему. Расположение частот по диагонали от правого верхнего угла к левому нижнему говорит об обратной связи.
Для построения корреляционной таблицы необходимо знать величины и границы интервалов по двум признакам Х и Y. Величина интервала и границы интервалов для факторного признака Х - Объем кредитных вложений известны из табл. 8. Для результативного признака Y - Сумма прибыли величина интервала определяется по формуле (1) при k = 4, ymax = 90,2 млн руб., ymin = 6,2 млн. руб.:
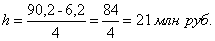
Границы интервалов ряда распределения результативного признака Y имеют следующий вид (табл. 9):
Таблица 9
| Номер группы | Нижняя граница, млн руб. | Верхняя граница, млн руб. |
|---|---|---|
| 1 | 6,2 | 27,2 |
| 2 | 27,2 | 48,2 |
| 3 | 48,2 | 69,2 |
| 4 | 69,2 | 90,2 |
Подсчитывая с использованием принципа полуоткрытого интервала [ ) число банков, входящих в каждую группу (частоты групп), получаем интервальный ряд распределения результативного признака (табл. 10).
Таблица 10
Распределение банков по сумме прибыли
| Группы банков по сумме прибыли, млн руб., x | Число банков, f |
|---|---|
| 6,2-27,2 | 4 |
| 27,2-48,2 | 5 |
| 48,2-69,2 | 14 |
| 69,2-90,2 | 7 |
| Итого | 30 |
Используя группировки по факторному и результативному признакам, строим корреляционную таблицу (табл. 11).
Таблица 11
Корреляционная таблица зависимости суммы прибыли банков от объема кредитных вложений
| Группы банков по размеру кредитных вложений, млн руб. | Группы банков по сумме прибыли, млн руб. | ||||
|---|---|---|---|---|---|
| 6,2-27,2 | 27,2-48,2 | 48,2-69,2 | 69,2-90,2 | Итого | |
| 40-90 | 2 | 1 | 3 | ||
| 90 - 140 | 2 | 2 | 2 | 6 | |
| 140- 190 | 2 | 10 | 12 | ||
| 190-240 | 2 | 7 | 9 | ||
| Итого | 4 | 5 | 14 | 7 | 30 |
Вывод. Анализ данных табл. 11 показывает, что распределение частот групп произошло вдоль диагонали, идущей из левого верхнего угла в правый нижний угол таблицы. Это свидетельствует о наличии прямой корреляционной связи между объемом кредитных вложений и суммой прибыли банков.
2. Измерение тесноты корреляционной связи с использованием коэффициента детерминации и эмпирического корреляционного отношения
Для измерения тесноты связи между факторным и результативным признаками рассчитывают специальные показатели - эмпирический коэффициент детерминации η2 и эмпирическое корреляционное отношение η.
Эмпирический коэффициент детерминации η2 оценивает, насколько вариация результативного признака Y объясняется вариацией фактора X (остальная часть вариации Y объясняется вариацией прочих факторов). Показатель η2 рассчитывается как доля межгрупповой дисперсии в общей дисперсии по формуле
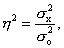 (9)
(9)
где - 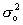 общая дисперсия признака
Y,
общая дисперсия признака
Y,
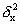 - межгрупповая (факторная)
дисперсия признака Y.
- межгрупповая (факторная)
дисперсия признака Y.
Значения показателя η2 изменяются в пределах 0 ≤ η2 ≤ 1. При отсутствии корреляционной связи между признаками Х и Y имеет место равенство η2 = 0, а при наличии функциональной связи между ними - равенство η2 = 1.
Общая дисперсия
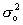 характеризует вариацию результативного
признака, сложившуюся под влиянием всех действующих на Y факторов
(систематических и случайных). Этот показатель вычисляется по формуле
характеризует вариацию результативного
признака, сложившуюся под влиянием всех действующих на Y факторов
(систематических и случайных). Этот показатель вычисляется по формуле
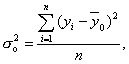 (10)
(10)
где yi - индивидуальные значения результативного признака;
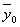 - общая средняя значений
результативного признака;
- общая средняя значений
результативного признака;
n - число единиц совокупности.
Общая средняя 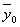 вычисляется
как средняя арифметическая простая по всем единицам совокупности:
вычисляется
как средняя арифметическая простая по всем единицам совокупности:
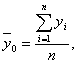 (11)
(11)
или как средняя взвешенная по частоте групп интервального ряда:
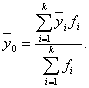 (12)
(12)
Для вычисления 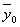 удобно использовать
формулу (11), так как в табл. 8 (графы 3 и 4 итоговой строки) имеются значения
числителя и знаменателя формулы.
удобно использовать
формулу (11), так как в табл. 8 (графы 3 и 4 итоговой строки) имеются значения
числителя и знаменателя формулы.
Расчет 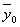 по формуле (11):
по формуле (11):
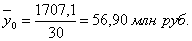
Для расчета общей дисперсии
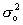 применяется вспомогательная таблица 12.
применяется вспомогательная таблица 12.
Расчет общей дисперсии по формуле (10):
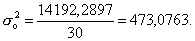
Общая дисперсия может быть также рассчитана по формуле
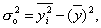
где - 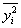 средняя из квадратов
значений результативного признака,
средняя из квадратов
значений результативного признака,
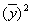 - квадрат средней значений
результативного признака.
- квадрат средней значений
результативного признака.
Для демонстрационного примера
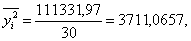
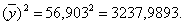
Тогда
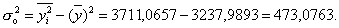
Межгрупповая дисперсия 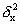 измеряет
систематическую вариацию результативного признака, обусловленную
влиянием признака-фактора X (по которому произведена группировка).
измеряет
систематическую вариацию результативного признака, обусловленную
влиянием признака-фактора X (по которому произведена группировка).
Таблица 12
Вспомогательная таблица для расчета общей дисперсии
| Номер банка п/п | Прибыль, млн руб. | 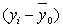 |
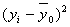 |
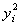 |
|---|---|---|---|---|
| 1 | 45,1 | -11,803 | 139,3187 | 2034,01 |
| 2 | 6,2 | -50,703 | 2570,8280 | 38,44 |
| 3 | 67,0 | 10,097 | 101,9427 | 4489,00 |
| 4 | 27,3 | -29,603 | 876,3573 | 745,29 |
| 5 | 62,5 | 5,597 | 31,3227 | 3906,25 |
| 6 | 60,0 | 3,097 | 9,5893 | 3600,00 |
| 7 | 16,9 | -40,003 | 1600,2667 | 285,61 |
| 8 | 20,9 | -36,003 | 1296,2400 | 436,81 |
| 9 | 65,0 | 8,097 | 65,5560 | 4225,00 |
| 10 | 16,0 | -40,903 | 1673,0827 | 256,00 |
| 11 | 69,0 | 12,097 | 146,3293 | 4761,00 |
| 12 | 35,0 | -21,903 | 479,7560 | 1225,00 |
| 13 | 53,4 | -3,503 | 12,2733 | 2851,56 |
| 14 | 66,2 | 9,297 | 86,4280 | 4382,44 |
| 15 | 56,0 | -0,903 | 0,8160 | 3136,00 |
| 16 | 58,0 | 1,097 | 1,2027 | 3364,00 |
| 17 | 47,0 | -9,903 | 98,0760 | 2209,00 |
| 18 | 64,7 | 7,797 | 60,7880 | 4186,09 |
| 19 | 46,2 | -10,703 | 114,5613 | 2134,44 |
| 20 | 53,7 | -3,203 | 10,2613 | 2883,69 |
| 21 | 67,0 | 10,097 | 101,9427 | 4489,00 |
| 22 | 68,0 | 11,097 | 123,1360 | 4624,00 |
| 23 | 70,0 | 13,097 | 171,5227 | 4900,00 |
| 24 | 80,1 | 23,197 | 538,0853 | 6416,01 |
| 25 | 67,7 | 10,797 | 116,5680 | 4583,29 |
| 26 | 72,0 | 15,097 | 227,9093 | 5184,00 |
| 27 | 84,0 | 27,097 | 734,2293 | 7056,00 |
| 28 | 87,0 | 30,097 | 905,8093 | 7569,00 |
| 29 | 90,2 | 33,297 | 1108,6680 | 8136,04 |
| 30 | 85,0 | 28,097 | 789,4227 | 7225,00 |
| Итого | 1707,1 | 1650,197 | 14192,2897 | 111331,97 |
Воздействие фактора Х на результативный признак Y
проявляется в отклонении групповых средних
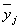 от общей средней
от общей средней
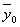 . Показатель
. Показатель
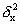 вычисляется по формуле
вычисляется по формуле
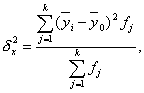 (13)
(13)
где - 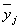 групповые средние;
групповые средние;
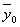 - общая средняя;
- общая средняя;
fj - число единиц в j-й группе;
k - число групп.
Для расчета межгрупповой дисперсии
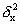 строится вспомогательная таблица 13.
При этом используются групповые средние значения
строится вспомогательная таблица 13.
При этом используются групповые средние значения
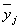 из табл. 8 (графа 5).
из табл. 8 (графа 5).
Таблица 13
Вспомогательная таблица для расчета межгрупповой дисперсии
| Группы банков по размеру кредитных вложений, млн руб. | Число банков, fj | Среднее значение 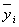 в группе в группе |
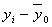 |
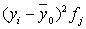 |
|---|---|---|---|---|
| 40-90 | 3 | 16,800 | -40,103 | 4824,8320 |
| 90-140 | 6 | 40,216 | -16,687 | 1670,6690 |
| 140-190 | 12 | 59,283 | 2,380 | 67,9728 |
| 190-240 | 9 | 78,222 | 21,319 | 4090,4552 |
| Итого | 30 | 10653,9291 |
Расчет межгрупповой дисперсии
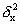 по формуле (13):
по формуле (13):
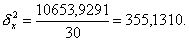
Расчет эмпирического коэффициента детерминации η2 по формуле (9):
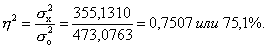
Вывод. 75,1% вариации суммы прибыли банков обусловлено вариацией объема кредитных вложений, а 24,9% - влиянием прочих неучтенных факторов.
Эмпирическое корреляционное отношение η оценивает тесноту связи между факторным и результативным признаками и вычисляется по формуле
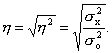 (14)
(14)
Значение показателя изменяются в пределах 0 ≤ η ≤ 1. Чем ближе значение η к 1, тем теснее связь между признаками. Для качественной оценки тесноты связи на основе η служит шкала Чэддока (табл. 14).
Таблица 14
Шкала Чэддока
| η | 0,1-0,3 | 0,3-0,5 | 0,5-0,7 | 0,7-0,9 | 0,9-0,99 |
|---|---|---|---|---|---|
| Характеристика силы связи | Слабая | Умеренная | Заметная | Тесная | Весьма тесная |
Расчет эмпирического корреляционного отношения η по формуле (14):
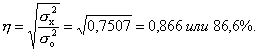
Вывод. Согласно шкале Чэддока связь между объемом кредитных вложений и суммой прибыли банков является тесной.