Раздел I. Методические рекомендации к выполнению статистических расчетов
Раздел II. Образец выполнения и оформления заданий 1-3 курсовых и контрольных работ
Задание 1
По исходным данным (табл. 1) необходимо выполнить следующее.
1. Построить статистический ряд распределения фирм по среднесписочной численности менеджеров, образовав шесть групп с равными интервалами.
2. Графическим методом и путем расчетов определить значения моды и медианы полученного ряда распределения.
3. Рассчитать характеристики ряда распределения: среднюю арифметическую, среднее квадратическое отклонение, коэффициент вариации.
4. Вычислить среднюю арифметическую по исходным данным (табл. 1), сравнить ее с аналогичным показателем, рассчитанным в п. 3 для интервального ряда распределения. Объяснить причину их расхождения.
Сделать выводы по результатам выполнения задания 1.
Выполнение задания 1
Целью выполнения данного задания является изучение состава и структуры выборочной совокупности фирм путем построения и анализа статистического ряда распределения фирм по признаку Среднесписочная численность менеджеров.
1. Построение интервального ряда распределения фирм по среднесписочной численности менеджеров
Для построения интервального ряда распределения определяем величину интервала h по формуле:
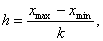
где xmax, xmin - наибольшее и наименьшее значения признака в исследуемой совокупности, k - число групп интервального ряда.
При заданных k = 6, xmax = 50 чел. и xmin = 20 чел.

При h = 5 чел. границы интервалов ряда распределения имеют следующий вид:
Таблица 2
| Номер группы | Нижняя граница, чел. | Верхняя граница, чел. |
|---|---|---|
| 1 | 20 | 25 |
| 2 | 25 | 30 |
| 3 | 30 | 35 |
| 4 | 35 | 40 |
Определяем число фирм, входящих в каждую группу, используя принцип полуоткрытого интервала [ ), согласно которому фирмы со значениями признаков, которые служат одновременно верхними и нижними границами смежных интервалов (25, 30, 35, 40 и 45 чел.), будем относить ко второму из смежных интервалов.
Для определения числа фирм в каждой группе строим разработочную таблицу 3 (данные графы 4 потребуются при выполнении задания 2).
Таблица 3
Разработочная таблица для построения интервального ряда распределения и аналитической группировки
| Группы фирм по среднесписочной численности менеджеров, чел. | Номер фирмы | Среднесписочная численность менеджеров, чел. | Объем продаж, млн руб. |
|---|---|---|---|
| 20-25 | 3 | 20 | 2,50 |
| 12 | 22 | 2,60 | |
| 4 | 24 | 2,60 | |
| Всего | 3 | 66 | 7,70 |
| 25-30 | 13 | 25 | 2,80 |
| 2 | 26 | 2,80 | |
| 10 | 27 | 2,90 | |
| 7 | 28 | 2,90 | |
| Всего | 4 | 106 | 11,40 |
| 30-35 | 5 | 30 | 3,00 |
| 17 | 31 | 3,00 | |
| 20 | 31 | 3,00 | |
| 15 | 32 | 3,10 | |
| 6 | 33 | 3,10 | |
| 18 | 33 | 3,30 | |
| Всего | 6 | 190 | 18,50 |
| 35-40 | 1 | 35 | 3,30 |
| 8 | 35 | 3,40 | |
| 14 | 35 | 3,35 | |
| 11 | 36 | 3,30 | |
| 21 | 36 | 3,35 | |
| 22 | 36 | 3,45 | |
| 23 | 37 | 3,47 | |
| 24 | 37 | 3,50 | |
| 25 | 38 | 3,60 | |
| 26 | 39 | 3,70 | |
| Всего | 10 | 364 | 34,42 |
| 40-45 | 19 | 41 | 3,50 |
| 9 | 42 | 3,60 | |
| 27 | 43 | 3,60 | |
| 28 | 44 | 4,00 | |
| Всего | 4 | 170 | 14,70 |
| 45-50 | 29 | 46 | 3,90 |
| 30 | 48 | 3,80 | |
| 16 | 50 | 4,00 | |
| Всего | 3 | 144 | 11,70 |
| Итого | 30 | 1040 | 98,42 |
На основе групповых итоговых строк «Всего» табл. 3 формируем итоговую таблицу 4, представляющую интервальный ряд распределения фирм по среднесписочной численности менеджеров.
Таблица 4
Распределение фирм по среднесписочной численности менеджеров
| Номер группы | Группы фирм по среднесписочной численности менеджеров, чел., х | Число фирм, f |
|---|---|---|
| 1 | 20-25 | 3 |
| 2 | 25-30 | 4 |
| 3 | 30-35 | 6 |
| 4 | 35-40 | 10 |
| 5 | 40-45 | 4 |
| 6 | 45-50 | 3 |
| ИТОГО | 30 |
Приведем еще три характеристики полученного ряда распределения
- частоты групп в относительном выражении, накопленные (кумулятивные)
частоты Sj, получаемые путем последовательного суммирования
частот всех предшествующих (j - 1) интервалов, и накопленные частости,
рассчитываемые по формуле 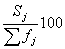 .
.
Таблица 5
Структура фирм по среднесписочной численности менеджеров
| № группы | Группы фирм по среднесписочной численности менеджеров, чел. | Число фирм, f | Накопленная частота, Sj | Накопленная частость, % | |
|---|---|---|---|---|---|
| в абсолютном выражении | в % к итогу | ||||
| 1 | 20-25 | 3 | 10 | 3 | 10 |
| 2 | 25-30 | 4 | 13 | 7 | 23 |
| 3 | 30-35 | 6 | 20 | 13 | 43 |
| 4 | 35-40 | 10 | 34 | 23 | 77 |
| 5 | 40-45 | 4 | 13 | 27 | 90 |
| 6 | 45-50 | 3 | 10 | 30 | 100 |
| ИТОГО | 30 | 100 | |||
Вывод: Анализ интервального ряда распределения изучаемой совокупности фирм показывает, что распределение фирм по среднесписочной численности менеджеров не является равномерным: преобладают фирмы со среднесписочной численностью менеджеров от 35 чел. до 40 чел. (это 10 фирм, доля которых составляет 34%); самые малочисленные группы фирм имеют 25-30 чел. и 45-50 чел., каждая из которых включает три фирмы, что составляет по 10% от общего числа фирм.
2. Нахождение моды и медианы полученного интервального ряда распределения графическим методом и путем расчетов
Для определения моды графическим методом строим по данным табл. 4 гистограмму распределения фирм по изучаемому признаку.

Рис. 1. Определение моды графическим методом
Расчет конкретного значения моды для интервального ряда распределения производится по формуле:
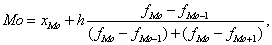
где хМо - нижняя граница модального интервала;
h - величина модального интервала;
fMo - частота модального интервала;
fMo-1 - частота интервала, предшествующего модальному;
fMo+1 - частота интервала, следующего за модальным.
Согласно табл. 4 модальным интервалом построенного ряда является интервал 35-40 чел., так как он имеет наибольшую частоту (f4 = 10). Расчет моды:

Вывод. Для рассматриваемой совокупности фирм наиболее распространенная среднесписочная численность менеджеров характеризуется средней величиной 37 человек.
Для определения медианы графическим методом строим по данным табл. 5 (графы 2 и 5) кумуляту распределения фирм по изучаемому признаку.

Рис. 2. Определение медианы графическим методом
Расчет конкретного значения медианы для интервального ряда распределения производится по формуле:
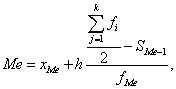
где хМе - нижняя граница медианного интервала;
h - величина медианного интервала;
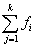 - сумма всех частот;
- сумма всех частот;
fMe - частота медианного интервала;
SMe-1 - кумулятивная (накопленная) частота интервала, предшествующего медианному.
Определяем медианный интервал, используя графу 5 табл. 5. Медианным
интервалом является интервал 35-40 чел., так как именно в этом интервале
накопленная частота Sj = 23 впервые превышает полусумму
всех частот  .
.
Расчет медианы:

Вывод. В рассматриваемой совокупности фирм половина фирм имеют среднесписочную численность менеджеров не более 36 человек, а другая половина - не менее 36 человек.
3. Расчет характеристик ряда распределения
Для расчета характеристик ряда распределения
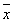 , s, s2, Vs
на основе табл. 5 строим вспомогательная таблица 6 (
, s, s2, Vs
на основе табл. 5 строим вспомогательная таблица 6 (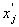 - середина интервала).
- середина интервала).
Таблица 6
Расчетная таблица для нахождения характеристик ряда распределения
| Группы фирм по среднесписочной численности менеджеров, чел. | Середина интервала, 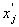 |
Число банков, fj | 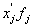 |
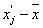 |
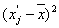 |
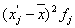 |
|---|---|---|---|---|---|---|
| 20-25 | 22,5 | 3 | 67,5 | -12,833 | 164,6859 | 494,0577 |
| 25-30 | 27,5 | 4 | 110,0 | -7,833 | 61,3559 | 245,4236 |
| 30-35 | 32,5 | 6 | 195,0 | -2,833 | 8,0259 | 48,1553 |
| 35-40 | 37,5 | 10 | 375,0 | 2,167 | 4,6959 | 46,9589 |
| 40-45 | 42,5 | 4 | 170,0 | 7,167 | 51,3659 | 205,4636 |
| 45-50 | 47,5 | 3 | 142,5 | 12,167 | 148,0359 | 444,1077 |
| ИТОГО | 30 | 1060,0 | 1484,1668 |
Рассчитаем среднюю арифметическую взвешенную:

Рассчитаем среднее квадратическое отклонение:

Рассчитаем дисперсию:
s2 = 7,03362 = 49,47222.
Рассчитаем коэффициент вариации:

Вывод: Анализ полученных значений показателей
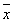 и s говорит о том, что средняя
величина среднесписочной численности менеджеров составляет 35 чел., отклонение
от этой величины в ту или иную сторону составляет в среднем 7 чел. (или
19,9%), наиболее характерная среднесписочная численность менеджеров находится
в пределах от 28 до 42 чел. (диапазон
и s говорит о том, что средняя
величина среднесписочной численности менеджеров составляет 35 чел., отклонение
от этой величины в ту или иную сторону составляет в среднем 7 чел. (или
19,9%), наиболее характерная среднесписочная численность менеджеров находится
в пределах от 28 до 42 чел. (диапазон 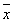 ± σ).
± σ).
Значение Vs = 19,9% не превышает 33%, следовательно,
вариация среднесписочной численности менеджеров в исследуемой совокупности
фирм незначительна и совокупность по данному признаку однородна. Расхождение
между значениями 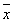 , Mo и Me незначительно
(
, Mo и Me незначительно
(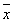 = 35 чел., Мо = 37 чел., Ме = 36 чел.),
что подтверждает вывод об однородности совокупности фирм. Таким образом,
найденное среднее значение среднесписочной численности менеджеров (35 чел.)
является типичной, надежной характеристикой исследуемой совокупности фирм.
= 35 чел., Мо = 37 чел., Ме = 36 чел.),
что подтверждает вывод об однородности совокупности фирм. Таким образом,
найденное среднее значение среднесписочной численности менеджеров (35 чел.)
является типичной, надежной характеристикой исследуемой совокупности фирм.
4. Вычисление средней арифметической по исходным данным о среднесписочной численности менеджеров фирм
Для расчета применяется формула средней арифметической простой:

Причина расхождения средних величин, рассчитанных по исходным
данным (34,67 чел.) и по интервальному ряду распределения (35,33 чел.),
заключается в том, что в первом случае средняя определяется по фактическим
значениям исследуемого признака для всех 30 фирм, а во втором случае
в качестве значений признака берутся середины интервалов
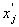 и, следовательно, значение средней будет
менее точным. Вместе с тем, при округлении обеих рассматриваемых величин
их значения совпадают (35 чел.), что говорит о достаточно равномерном распределении
численности менеджеров внутри каждой группы интервального ряда.
и, следовательно, значение средней будет
менее точным. Вместе с тем, при округлении обеих рассматриваемых величин
их значения совпадают (35 чел.), что говорит о достаточно равномерном распределении
численности менеджеров внутри каждой группы интервального ряда.