В начало

Литература

Задание 3

По результатам выполнения задания 1 с вероятностью 0,954 необходимо определить:

1) ошибку выборки для средней величины среднесписочной численности менеджеров, а также границы, в которых будет находиться генеральная средняя.

2) ошибку выборки доли фирм со среднесписочной численностью менеджеров 40 человек и более, а также границы, в которых будет находиться генеральная доля фирм.

Выполнение задания 3

Целью выполнения данного задания является определение для генеральной совокупности фирм региона границ, в которых будут находиться средняя величина среднесписочной численности менеджеров и доля фирм со среднесписочной численностью менеджеров не менее 40 человек.

1. Определение ошибки выборки для величины среднесписочной численности менеджеров, а также границ, в которых будет находиться генеральная средняя

Применяя выборочный метод наблюдения, необходимо рассчитать ошибки выборки (ошибки репрезентативности), так как генеральные и выборочные характеристики, как правило, не совпадают, а отклоняются на некоторую величину е.

Принято вычислять два вида ошибок выборки - среднюю 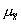и предельную .

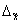Для расчета средней ошибки выборки 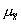применяются различные формулы в зависимости от вида и способа отбора единиц из генеральной совокупности в выборочную.

Для собственно-случайной и механической выборки с бесповторным способом отбора средняя ошибка 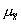для выборочной средней 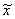определяется по формуле

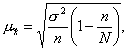
где σ² - общая дисперсия выборочных значений признаков;

N- число единиц в генеральной совокупности;

n - число единиц в выборочной совокупности.

Предельная ошибка выборки 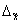определяет границы, в пределах которых будет находиться генеральная средняя:

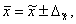
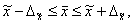
где 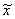- выборочная средняя;

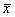- генеральная средняя.

Предельная ошибка выборки 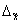кратна средней ошибке с коэффициентом кратности t (называемым коэффициентом доверия):

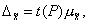
Коэффициент кратности t зависит от значения доверительной вероятности Р, гарантирующей вхождение генеральной средней в интервал 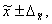называемый доверительным интервалом.

Наиболее часто используемые доверительные вероятности Р и соответствующие им значения t задаются следующим образом (табл. 14):

Таблица 14

По условию задания 2 выборочная совокупность насчитывает 30 фирм, выборка 10% механическая, следовательно, генеральная совокупность включает 300 фирм. Выборочная средняя 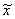, дисперсия σ² определены в задании 1 (п. 3). Значения параметров, необходимых для решения задачи, представлены в табл. 15:

Таблица 15

P	t	n	N		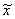σ2
0,954	2	30	300	35,33	49,47

Рассчитаем среднюю ошибку выборки:

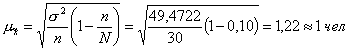
Рассчитаем предельную ошибку выборки:

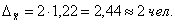
Определим доверительный интервал для генеральной средней:

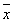35,33 - 2,44 ≤ ≤ 35,33 + 2,44

32,89 ≤ 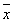≤ 37,77

или

33 чел. ≤ 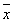≤ 38; чел.

Вывод. На основании проведенного выборочного обследования с вероятностью 0,954 можно утверждать, что для генеральной совокупности фирм средняя величина среднесписочной численности менеджеров находится в пределах от 33 до 38 человек.

2. Определение ошибки выборки для доли фирм со среднесписочной численностью менеджеров 40 человек и более, а также границ, в которых будет находиться генеральная доля

Доля единиц выборочной совокупности, обладающих тем или иным заданным свойством, выражается формулой

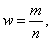
где m - число единиц совокупности, обладающих заданным свойствам;

n - общее число единиц в совокупности.

Для собственно-случайной и механической выборки с бесповторным способом отбора предельная ошибка выборки Δ_w доли единиц, обладающих заданным свойством, рассчитывается по формуле

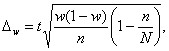
где w - доля единиц совокупности, обладающих заданным свойством;

(1 - w) - доля единиц совокупности, не обладающих заданным свойством,

N - число единиц в генеральной совокупности,

n - число единиц в выборочной совокупности.

Предельная ошибка выборки Δ_w определяет границы, в пределах которых будет находиться генеральная доля р единиц, обладающих исследуемым признаком:

w - Δ_w ≤ p ≤ w + Δ_w.

По условию задания 3 исследуемым свойством фирм являйся равенство или превышение среднесписочной численности менеджеров величины 40 человек.

Число фирм с данным свойством определяется из табл. 3 (графа 3):

m = 7

Рассчитаем выборочную долю:

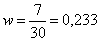
Рассчитаем предельную ошибку выборки для доли:

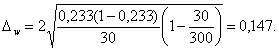
Определим доверительный интервал генеральной доли:

0,233 - 0,147 ≤ p ≤ 0,233 + 0,147

0,086 ≤ p ≤ 0,38

или

8,6% ≤ p ≤ 38%

Вывод. С вероятностью 0,954 можно утверждать, что в генеральной совокупности фирм региона доля фирм со среднесписочной численностью менеджеров 40 человек и более будет находиться в пределах от 8,6% до 38%.