В начало

Литература

Задание 3

По результатам выполнения задания 1 с вероятностью 0,954 необходимо определить:

1. Ошибку выборки средней величины объема кредитных вложений банков и границы, в которых будет находиться генеральная средняя.

2. Ошибку выборки доли банков с объемом кредитных вложений 175 млн руб. и выше, а также границы, в которых будет находиться генеральная доля.

3. Необходимый объем выборки при заданной предельной ошибке выборки, равной 10 млн руб.

Выполнение задания 3

Целью выполнения данного задания является определение для генеральной совокупности коммерческих банков региона границ, в которых будут находиться величина среднего объема кредитных вложений банков и доля банков с объемом кредитных вложений не менее 175 млн руб.

1. Определение ошибки выборки для среднего объема кредитных вложений банков и границ, в которых будет находиться генеральная средняя

Применение выборочного метода наблюдения всегда связано с установлением степени достоверности оценок показателей генеральной совокупности, полученных на основе значений показателей выборочной совокупности. Достоверность этих оценок зависит от репрезентативности выборки, то есть от того, насколько полно и адекватно представлены в выборке статистические свойства генеральной совокупности. Как правило, генеральные и выборочные характеристики не совпадают, а отклоняются на некоторую величину е, которую называют ошибкой выборки (ошибкой репрезентативности).

Значения признаков единиц, отобранных из генеральной совокупности в выборочную, всегда случайны, поэтому и статистические характеристики выборки случайны, следовательно, и ошибки выборки также случайны. Ввиду этого принято вычислять два вида ошибок - среднюю 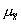и предельную .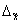

Средняя ошибка выборки 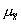- это среднее квадратическое отклонение всех возможных значений выборочной средней от генеральной средней, то есть от своего математического ожидания .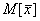

Величина средней ошибки выборки рассчитывается дифференцированно (по различным формулам) в зависимости от вида и способа отбора единиц из генеральной совокупности в выборочную.

Для собственно-случайной и механической выборки с бесповторным способом отбора средняя ошибка 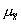выборочной средней 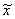определяется по формуле

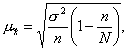(15)

где σ² - общая дисперсия выборочных значений признаков;

N- число единиц в генеральной совокупности;

n - число единиц в выборочной совокупности.

Предельная ошибка выборки 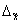определяет границы, в пределах которых будет находиться генеральная средняя:

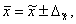
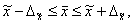(16)

где 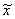- выборочная средняя;

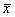- генеральная средняя.

Границы задают доверительный интервал генеральной средней, то есть случайную область значений, которая с вероятностью Р гарантированно содержит значение генеральной средней. Эту вероятность Р называют доверительной вероятностью или уровнем надежности.

В экономических исследованиях чаще всего используются доверительные вероятности Р = 0,954, Р = 0,997, реже Р = 0,683.

В математической статистике доказано, что предельная ошибка выборки D кратна средней ошибке μ с коэффициентом кратности t (называемым коэффициентом доверия), который зависит от значения доверительной вероятности Р. Для предельной ошибки выборочной средней 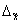это теоретическое положение выражается формулой

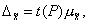(17)

Значения t вычислены заранее для различных доверительных вероятностей Р и протабулированы (таблицы функции Лапласа Ф). Для наиболее часто используемых уровней надежности Р значения t задаются следующим образом (табл. 15):

Таблица 15

По условию демонстрационного примера выборочная совокупность насчитывает 30 банков, выборка 20% механическая, следовательно, генеральная совокупность включает 150 банков.

Выборочная средняя 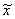, дисперсия σ² определены в задании 1 (п. 3). Значения параметров, необходимых для решения задачи, представлены в табл. 16:

Таблица 16

р	t	n	N		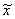σ2
0,954	2	30	150	160	2225

Расчет средней ошибки выборки по формуле (15):

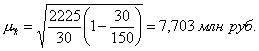
Расчет предельной ошибки выборки по формуле (17):

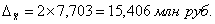
Определение по формуле (16) доверительного интервала для генеральной средней:

160 - 15,406 ≤ х ≤ 160 + 15,406,

144,594 млн руб. ≤ х ≤ 175,406 млн руб.

Вывод. На основании проведенного выборочного обследования коммерческих банков региона с вероятностью 0,954 можно утверждать, что для генеральной совокупности банков средний объем кредитных вложений банка находится в пределах от 144,59 млн руб. до 175,41 млн руб.

2. Определение ошибки выборки для доли банков с объемом кредитных вложений 175 млн руб. и выше, а также границ, в которых будет находиться генеральная доля

Доля единиц выборочной совокупности, обладающих тем или иным заданным свойством, выражается формулой

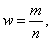(18)

где m - число единиц совокупности, обладающих заданным свойством;

n - общее число единиц в совокупности.

Для собственно-случайной и механической выборки с бесповторным способом отбора предельная ошибка выборки Δ_w доли единиц, обладающих заданным свойством, рассчитывается по формуле

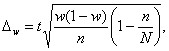(19)

где w - доля единиц совокупности, обладающих заданным свойством;

(1 - w) - доля единиц совокупности, не обладающих заданным свойством;

N - число единиц в генеральной совокупности;

n - число единиц в выборочной совокупности.

Предельная ошибка выборки Δ_w определяет границы, в пределах которых будет находиться генеральная доля р единиц, обладающих заданным свойством:

w – Δ_w < p < w + Δ_w. (20)

По условию задания 3 исследуемым свойством является равенство или превышение объема кредитных вложений банка величины 175 млн руб.

Число банков с заданным свойством определяется из табл. 3 (графа 3):

m = 11

Расчет выборочной доли по формуле (18):

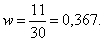
Расчет по формуле (19) предельной ошибки выборки для доли:

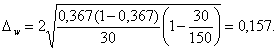
Определение по формуле (20) доверительного интервала генеральной доли:

0,367 - 0,157 ≤ р ≤ 0,367 + 0,157

0,21 ≤ р ≤ 0,524

или

21% ≤ р ≤ 52,4%.

Вывод. С вероятностью 0,954 можно утверждать, что в генеральной совокупности банков доля банков с объемом кредитных вложений 175 млн руб. и выше будет находиться в пределах от 21% до 52,4%.

3. Определение необходимого объема выборки с заданным значением допустимой предельной ошибки выборки, равной 10 млн руб.

Для собственно-случайной и механической выборки с бесповторным способом отбора необходимый объем выборки для средней количественного признака вычисляется по формуле

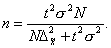(21)

По условию демонстрационного примера ошибка 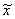выборки не должна превышать 10 млн руб. Параметры t, N и σ² известны из решений предыдущих задач.

Расчет необходимой численности выборки по формуле (21):

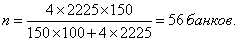
Вывод: Для того чтобы обеспечить для среднего объема кредитных вложений банков предельную ошибку выборки, равную 10 млн руб., необходимо из 150 банков, составляющих генеральную совокупность, отобрать в выборочную совокупность 56 банков.