В начало

Литература

Приложение 5. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

Линейное программирование - частный случай общей задачи оптимизации при наличии ограничений. Многие задачи планирования производственно-коммерческой деятельности предприятия сводятся к задачам линейного программирования. Задача линейного программирования на максимум в стандартной форме формулируется следующим образом.

Найти числа х₁, …, х_n такие, что

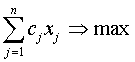, (1)

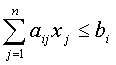, (2)

x_j ≥ 0, (3)

i = 1, …, m,

j = 1, …, n.

Например:

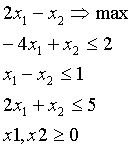(4)

В матричных обозначениях эта задача выглядит следующим образом:

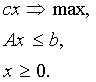(5)

Здесь с - n-мерный вектор-строка, х - m-мерный вектор-столбец, A - матрица порядка m × n.

Например:

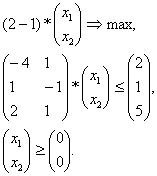(6)

Задача на минимум в стандартной форме записывается в виде:

,

,

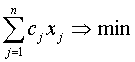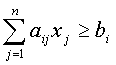x_j ≥ 0.

Или в матричном виде

cx → min,

Ax ≥ b,

x ≥ 0.

Функция сх от переменных x₁, ..., х_п называется целевой функцией.

Числа x₁, ..., x_n - векторы х, удовлетворяющие неравенствам

Ax ≤ b,

x ≥ 0.

в задаче на максимум или

Ax ≥ b,

x ≥ 0.

в задаче на минимум, называются множеством допустимых решений.

Иногда удобнее записывать задачу линейного программирования в канонической форме. Каноническая форма отличается от стандартной только записью ограничений. В канонической форме они записываются в следующем виде:

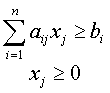, (7)

Задачу в канонической форме всегда можно привести к задаче в стандартной форме, записав равенства (7) в виде эквивалентной системы неравенств:

Ax ≤ b,

-Ax ≤ -b,

С другой стороны, задачу в стандартной форме тоже можно привести к задаче в канонической форме, введя дополнительные переменные z. Системы неравенств:

Ax ≤ b, и Ax + Iz = b, z ≥ 0

(где I - единичная матрица размерности m*m) эквивалентны. Например, задача (6) в канонической форме записывается как

,

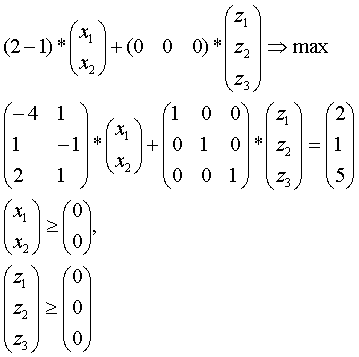или

.

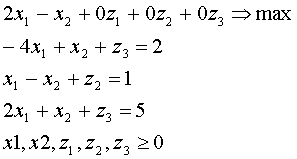Можно записать эту задачу проще, добавив нулевые элементы в вектор-строку коэффициентов целевой функции и столбцы в матрицу ограничений:

,

,

.

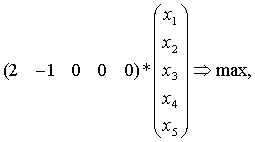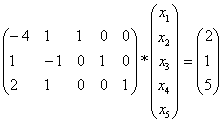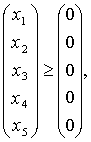Каждой задаче линейного программирования соответствует двойственная задача. Задаче на максимум в стандартной форме соответствует следующая двойственная задача.

Найти вектор у такой, что

yb → min,

yA ≥ c,

y ≥ 0.

или найти числа у₁, …, у_т такие, что

,

,

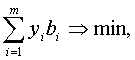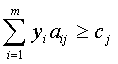y ≥ 0.

Стандартной задаче на минимум соответствует двойственная задача: Найти вектор у такой, что

yb → max,

уА ≤ с,

у ≥ 0.

или найти числа y_l, ..., y_m такие, что

,

,

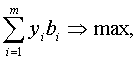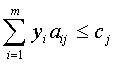у ≥ 0.

Связь между прямой и двойственной задачами описывается следующими теоремами:

1. Если прямая и двойственная задачи имеют допустимые решения (т. е. множества их допустимых решений не пусты), то обе они имеют и оптимальные решения у^*, х^*, причем

cx^* = y^*b

(оптимальные значения целевых функций прямой и двойственной задач равны),

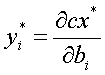
(при увеличении правой части ограничения b_i на единицу оптимальное значение целевой функции увеличится примерно на у_i единиц).

2. Для того чтобы допустимое решение прямой задачи линейного программирования 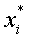, …, 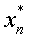было оптимальным, необходимо и достаточно, чтобы нашлось такое допустимое решение двойственной задачи 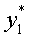, ..., 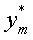, что

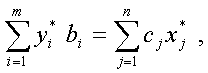
3. Если оптимальное решение задачи линейного программирования существует, то

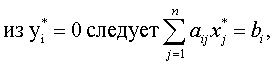
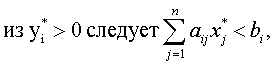
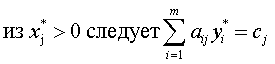
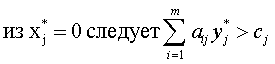
В общем случае это не обязательно, но обычно количество ненулевых элементов в векторе оптимального решения равно наименьшему из чисел: количество ограничений, количество переменных в прямой задаче.

Оптимального решения задачи линейного программирования не существует в любом из следующих случаев:

1. Если целевая функция не ограничена на множестве допустимых решений. Например:

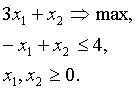
2. Если множество допустимых решений пусто, т. е. описывается системой несовместных неравенств. Например:

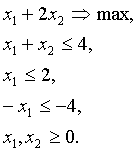
Обычно эти случаи являются следствием плохой постановки задачи.